【2】时间复杂度，空间复杂度——算法性能分析

判断一个算法性能的好坏，通常是考虑其时间复杂度和空间复杂度。
注意这里不是绝对的时间，同一个算法使用不同的编程语言，或在不同计算机上运行，它的实际时间、效率是不同的。
所以要将计算机硬件、软件等有关因素排除在外，只依赖于问题规模大小。

根据《算法导论》一书中，我们假定一种通用的单处理器计算模型——**随机访问机（RAM）**来作为我们的实现技术，算法可以用计算机程序来实现。在RAM模型中，指令一条接一条地执行，没有并发操作。

下图为RAM模型中常见指令，每条这样的指令所需时间都为常量。

时间复杂度

运行时间的计算

以插入排序算法为例

一个算法在特定输入上的运行时间是指执行的基本操作数或步数。
我们采用这样一个观点：执行每行伪代码需要常量时间。虽然一行与另一行可能需要不同数量的时间，但我们假定第i行的每次执行需要时间c_i，c_i是个常量。

该算法的运行时间是执行每条语句的运行时间之和。

对于给定规模的输入，①若输入数组已排好序，则出现最佳情况，该最佳情况的运行时间为：

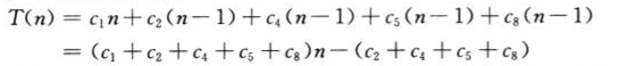
该运行时间可以表示为an+b，是n的线性函数。

②若数组已反向排序，则导致最坏情况，该最坏情况的运行时间为：

该运行时间可以表示为an²+bn+c，是n的二次函数。

我们在大多数情况下研究的都是最坏情况的运行时间。

对插入排序中的运行时间在进一步地做简化，我们真正感兴趣的是运行时间的增长率或增长量级，所以我们只考虑公式中最重要的项。当n很大时，低阶项相对来说不太重要，同时我们也忽略最重要的项的常系数。所以插入排序最坏情况下的时间复杂度可以表示为θ(n²)

渐近记号

θ记号

给出了一个函数的上界和下界


θ(g(n)）是一个集合，f(n)∈θ(g(n)），通常记为f(n)=θ(g(n)）

注意：任意常量是一个零阶多项式，所以任意常量函数可表示成θ(n⁰)或θ(1)

Ο记号

只有一个渐近上界时，使用Ο记号

Ω记号

只有一个渐近下界时，使用Ω记号

ο记号

表示非渐近紧确的上界

ω记号

表示非渐近紧确的下界

比较各种函数

实数中的许多关系性质也适用于渐近比较。

常见的复杂性的层次

空间复杂度

为了求解问题的实例而执行的计算步骤所需要的内存空间数目，不包括分配用来存储输入的空间。

许多问题都需要在时间与空间之间权衡。