粒子群算法的寻优算法-非线性函数极值寻优

1、算法介绍

1.1、算法概述

粒子群算法（particle swarm optimization，PSO）是计算智能领域中的一种生物启发式方法，属于群体智能优化算法的一种，常见的群体智能优化算法主要有如下几类：
　　（1）蚁群算法（Ant Colony Optimization，简称ACO）[1992年提出]；
　　（2）粒子群优化算法（Particle Swarm Optimization，简称PSO）[1995年提出]（简单易于实现，也是目前应用最为广泛的群体智能优化算法）；
　　（3）菌群优化算法（Bacterial Foraging Optimization，简称BFO）[2002年提出]；
　　（4）蛙跳算法（Shuffled Frog Leading Algorithm，简称SFLA）[2003年提出]；
　　（5）人工蜂群算法（Artificial Bee Colony Algorithm，简称ABC）[2005年提出]；
　　除了上述几种常见的群体智能算法以外，还有一些并不是广泛应用的群体智能算法，比如萤火虫算法、布谷鸟算法、蝙蝠算法以及磷虾群算法等等。

而其中的粒子群优化算法（PSO）源于对鸟类捕食行为的研究，鸟类捕食时，找到食物最简单有限的策略就是搜寻当前距离食物最近的鸟的周围。

1.2、算法思想

粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独的搜寻最优解，并将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解，粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置.

1.3、算法原理

PSO算法是基于群体的，根据对环境的适应度将群体中的个体移动到好的区域。然而它不对个体使用演化算子，而是将每个个体看作是D维搜索空间中的一个没有体积的微粒（点），在搜索空间中以一定的速度飞行，这个速度根据它本身的飞行经验和同伴的飞行经验来动态调整。第i个微粒表示为Xi= （xi1, xi2, …, xiD），它经历过的最好位置（有最好的适应值）记为Pi= （pi1, pi2, …, piD），也称为pbest。在群体所有微粒经历过的最好位置的索引号用符号g表示，即Pg，也称为gbest。微粒i的速度用Vi= （vi1, vi2, …, viD）表示。对每一代，它的第d维（1 ≤ d ≤ D）根据如下方程进行变化：
（1）vid = wvid+c1rand()(pid-xid)+c2∙Rand()(pgd-xid）
（2）xid = xid+vid
其中w为惯性权重（inertia weight），c1和c2为加速常数（acceleration constants），rand（）和Rand（）为两个在[0,1]范围里变化的随机值。
此外，微粒的速度Vi被一个最大速度Vmax所限制。如果当前对微粒的加速导致它的在某维的速度vid超过该维的最大速度vmax,d，则该维的速度被限制为该维最大速度vmax,d。
对公式（1）第一部分为微粒先前行为的惯性，第二部分为“认知（cognition）”部分，表示微粒本身的思考；第三部分为“社会（social）”部分，表示微粒间的信息共享与相互合作。
“认知”部分可以由Thorndike的效应法则（law of effect）所解释，即一个得到加强的随机行为在将来更有可能出现。这里的行为即“认知”，并假设获得正确的知识是得到加强的，这样的一个模型假定微粒被激励着去减小误差。
“社会”部分可以由Bandura的替代强化（vicarious reinforcement）所解释。根据该理论的预期，当观察者观察到一个模型在加强某一行为时，将增加它实行该行为的几率。即微粒本身的认知将被其它微粒所模仿。

惯性权重：

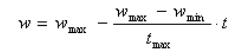
其中，w是惯性权重，wmax是