【新文速递20250427】一种具备双圆极化波束的低剖面自解耦折叠反射阵

欢迎加入电磁墨者QQ交流群(1036094484)，一起讨论交流电磁超表面的各类前沿文章和仿真技巧！期待各位电磁大侠的加入！
【文章来源】期刊：AWPL链接：https://ieeexplore.ieee.org/document/10820983
【作者简介】Dajun Ding，北京理工大学集成电路与电子学院毫米波与太赫兹技术

1.摘要

在本篇快报中，一种低剖面自解耦折叠反射阵列天线(SDFRA)被设计出来，该天线具备双圆极化波束独立控制，能够实现自旋角动量解耦合。特别的，天线所使用的介质基板被减少到3层。所提出来的SDFRA由接收辐射超表面(RTMS)、极化转换反射超表面(PCRM)以及一个磁电偶极子天线所构成。特殊的，RTMS能够反射x极化波并且透射其的正交极化波。此外，透射电磁波能够被分解成左圆极化(LHCP)和右圆极化(RHCP)。为了验证上述概念设计，样机天线进行了加工和测试。结果表明LHCP和RHCP的3dB增益带宽分别为20.89%和21.3%，最大实际增益分别为20.55dBic和20.52dBic(对应口径效率分别为：19.06%和19.19%)。实验结果与仿真结果吻合度较好。该天线所具备的宽带、低剖面、低成本等优势，使其为单频带双圆极化波束调控中提供了一种高效的解决方案。

2.核心内容

天线整体结构如下图所示，线极化磁电偶极子作为馈源天线，馈源发射出的x极化波被透射阵列反射后到达反射阵，该极化电磁波经过反射阵列后被转化为y极化波并被附加一个相位${\phi }_0$（共相位），随后从透射阵列透过并被分解成左圆极化和右圆极化波，由于透射单元旋转PB相位的共轭相位特性，对两种圆极化分别引入-${\phi }_1$和${\phi }_1$的相位（几何相位）。因此共相位和几何相位的联合调控可以实现两种圆极化的自解耦，其原理与传播相位和几何相位联合调控一致。
$$\begin{gathered} {\phi }_{lcp}={\phi }_0-{\phi }_1 \\ {\phi }_{rcp}={\phi }_0+{\phi }_1 \end{gathered}$$

从相位上分析如上式，从阵面偏转角分析可以得到下面关系：
$$\begin{gathered} {\theta }_{lcp}=\alpha -\beta \\ {\theta }_{rcp}=\alpha +\beta \end{gathered}$$
此外，由于折叠反射阵列性质，天线剖面也被缩短到了焦距的一半。

透射单元结构如下图所，是非常常见的接收辐射型透射超表面单元，由接收贴片、金属地和辐射贴片构成，该单元为线极化转线极化，辐射出去的线极化通过旋转金属结构实现两种圆极化的PB相位调节。


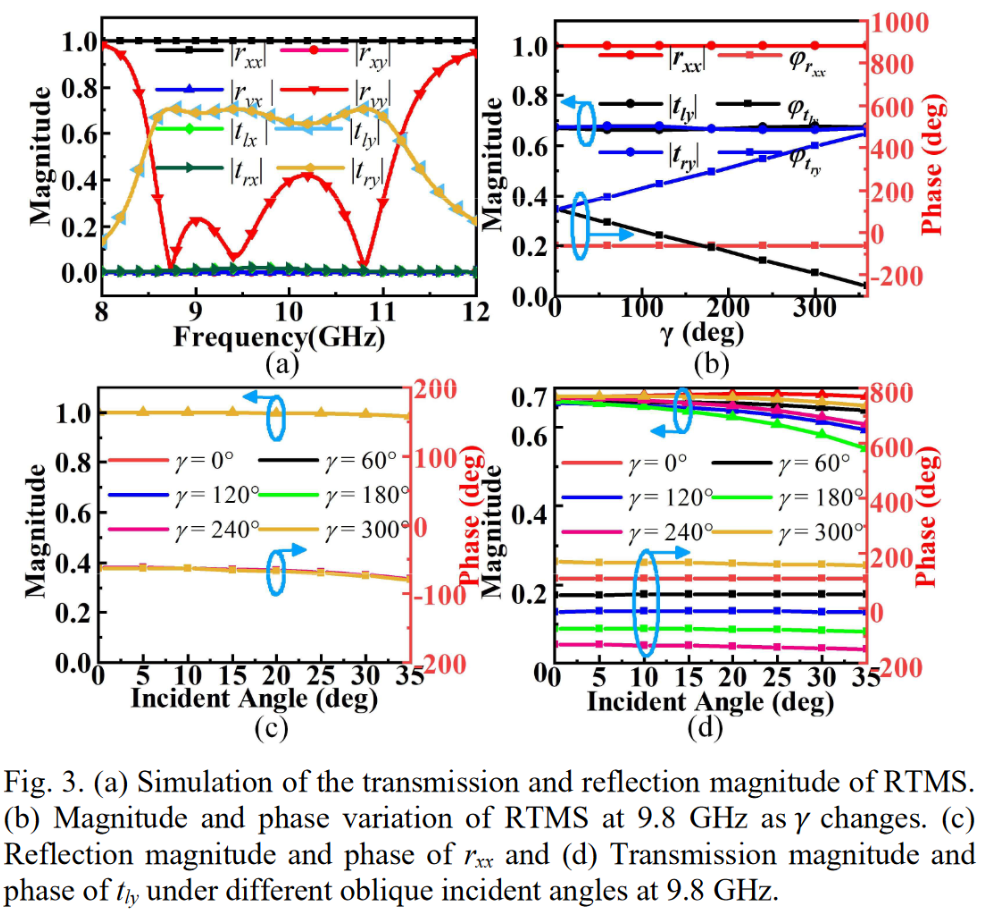
极化转换反射超表面结构与性能如下，采用常规的工字型结构，通过调节弧长角度实现相位调控，通过采用镜像法实现另外180度相位覆盖，能够实现线极化波的极化转换和全360度相位调控。

两层超表面阵列的相位排布按照上述配置图中偏转角度$\alpha =-5$和$\beta =-10$进行布阵，计算公式和排布结果如下(可以计算${\theta }_{lcp}=5$和${\theta }_{rcp}=-15$)
$$\begin{gathered} {\varphi }_{\text{PCRM}}(x_i,y_i)=k\left[r_i-\sin \alpha (x_i\cos {\phi }_0+y_i\sin {\phi }_0)\right] \\ {r}_i=\sqrt{(x_i-x_f{)}^2+(y_i-y_f{)}^2+z_f^2} \\ {\varphi }_{\text{RTMS}}(x_i,y_i)=k\left[-\sin \beta (x_i\cos {\phi }_0+y_i\sin {\phi }_0)\right] \end{gathered}$$

3.结果与讨论

加工样机天线图片如上图，并进行微波暗室测试天线性能，结果如下图，可见两种圆极化波束偏转角度准确，可以实现双圆极化波束的解耦调控。


该SDFRA具有低剖面态、宽带、高AE、高集成度等特点。在解耦自旋角动量的情况下，可以在单个频带内实现两种圆极化光束。最重要的是，与[29]相比，虽然它在H/D和AE方面略好于我们的工作，但我们的设计只使用了3层基板（不包括馈电天线和键合层）来实现类似的性能。低轮廓的SDFRA的重量和加工成本进一步降低。