算法学习第六天| 力扣454.四数相加II，383. 赎金信，15. 三数之和，18. 四数之和

今天学习了对哈希法的应用，加强了对题目的理解，对三数之和，四数之和做了对比，也明白了为什么三数之和与四数之和使用哈希法解题会比较麻烦，因为他们都涉及到了去重的问题，用哈希法去重会比较麻烦，代码实现会比较容易出错，替代的是双指针实现。而四数相加II因为不涉及到去重问题，用哈希法就显得简单得多。赎金信这题很像242.有效的字母异位词这题，是这题的变通，实现起来不算太难。

相关题目：
● 454. 四数相加 II：https://leetcode.cn/problems/4sum-ii/
● 383. 赎金信：https://leetcode.cn/problems/ransom-note/
● 15. 三数之和：https://leetcode.cn/problems/3sum/
● 18. 四数之和：https://leetcode.cn/problems/4sum/

关于454. 四数相加 II

题目描述：
● 给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ，使得 A[i] + B[j] + C[k] + D[l] = 0。
● 为了使问题简单化，所有的 A, B, C, D 具有相同的长度 N，且 0 ≤ N ≤ 500 。所有整数的范围在 -2^28 到 2^28 - 1 之间，最终结果不会超过 2^31 - 1 。

该题的思路：
● 该题和四数之和相比简单很多，因为该题有四个不同的数组，只要实现A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑去重的问题，而A[i] + B[j] + C[k] + D[l] = 0等价于A[i] + B[j]=-（C[k] + D[l]），若把A[i] + B[j]当作一个数sum1，把C[k] + D[l]当作另一个数sum2，那么这题就变为了sum1+sum2=0两数之和的形式了。
● 有人就疑问，考虑到了A[i] + B[j]=-（C[k] + D[l]），那么其他形式的情况呢，比如A[i]+C[k]=-（B[j] + D[l]）等这样的，其实A[i],B[j],C[k],D[I]在这里只是变量，A[i]也可以直接当作B[j],这样想的话，A[i] + B[j]=-（C[k] + D[l]）就包括所有情况了。
● 转化为两数之和的形式后，那么就好办了
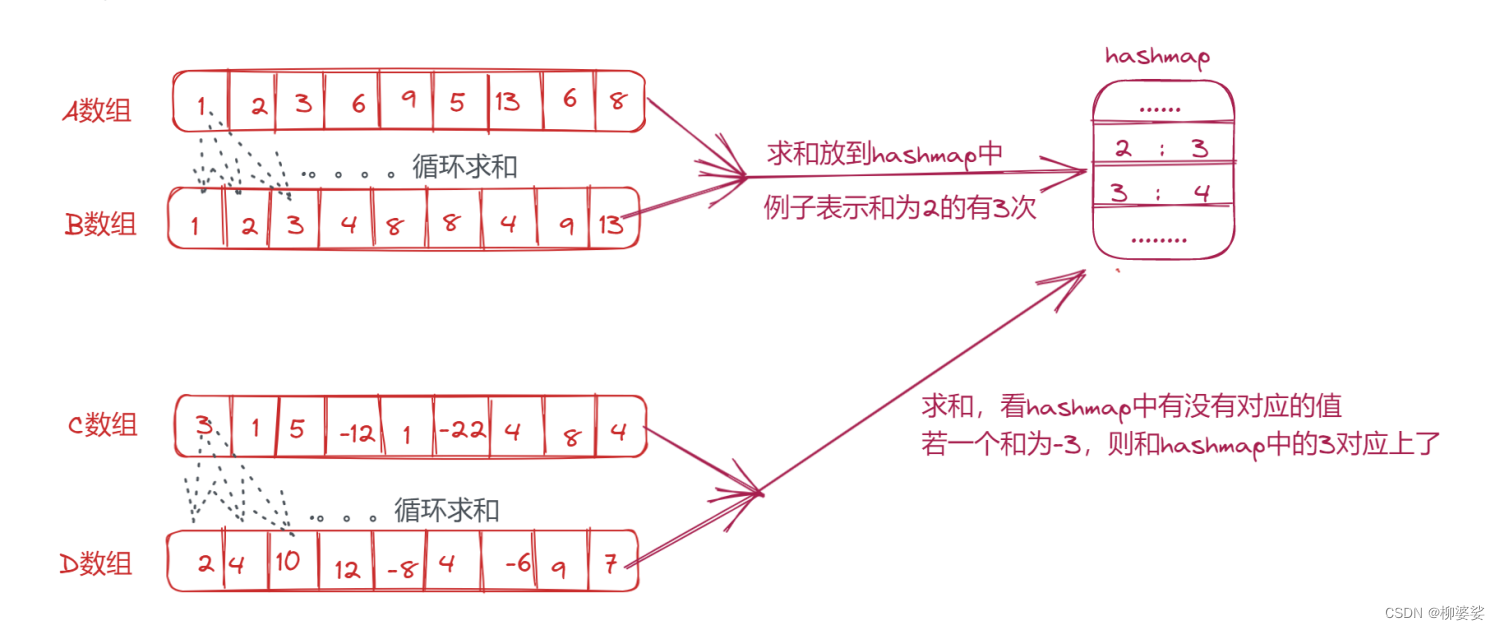
● 首先循环求出A数组和B数组的和所有情况和各自出现的次数，用哈希表hashmap1保存起来，key保存两个数组的和，value保存该和出现的次数。
● 再遍历大C和大D数组，求和，并与hashmap1比较，看-（c+d）在哈希表中是否存在，如果存在就记录次数+1，并把hashmap1中对应和的次数-1
● 最后返回记录好的次数即可。

代码实现：

class Solution {
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        //用于统计A和B的和的值和次数
        HashMap<Integer, Integer> sumHashMap12 = new HashMap<>();
        //最终的结果
        int count = 0;

        //循环求出和的所有
        for (int num1 : nums1) {
            for (int num2 : nums2) {
                int temp = num1 + num2;
                if (sumHashMap12.containsKey(temp)) {
                    sumHashMap12.put(temp, sumHashMap12.get(temp) + 1);
                } else {
                    sumHashMap12.put(temp, 1);
                }
            }
        }

        //遍历C和D，看是否有满足a+b=-(c+d)的，有就次数+1
        for (int num3 : nums3) {
            for (int num4 : nums4) {
                int temp = num3 + num4;
                if (sumHashMap12.containsKey(0 - temp)) {
                    count += sumHashMap12.get(0 - temp);
                }
            }
        }

        return count;
    }
}

关于383. 赎金信

题目描述
● 给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成，返回 true ；否则返回 false。
● (题目说明：为了不暴露赎金信字迹，要从杂志上搜索各个需要的字母，组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)
● 注意：
● 你可以假设两个字符串均只含有小写字母。
● canConstruct(“a”, “b”) -> false
canConstruct(“aa”, “ab”) -> false
canConstruct(“aa”, “aab”) -> true

该题的思路：
● 该题其实就是看magazine字符串中的字符足不足够组成ransom字符串，前提是magazine字符串中的字符只能使用一次，不能重复使用；也就是说，我们需要知道magazine字符串有什么字符和字符的次数，那么我们就可以用一个哈希表hashmap来记录magazine的情况，key为字符，value为对应字符的次数。
● 然后再遍历ransom字符串，与hashmap中的字符比较，若有不相同的，直接false；若相同，则把hashmap中对应字符的次数-1。
● 最后再次检查hashmap的各个value，若没有小于0的，则true，若有小于0的，则false。
● 但题目说了两个字符串均只含有小写字母，则我们可以用一个26大小的数组进行简化操作，通过对字符-'a’的操作得到再数组的位置，在位置上的值就是该字符的次数。

代码实现

//优化，用26大小数组进行简化
class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        //用于存放26个小写字母对应位置，值是字母出现的次数
        int[] ints = new int[26];

        //若ransomNote的长度比magazine大，则肯定不满足
        if (ransomNote.length()>magazine.length()){
            return false;
        }

        //统计magazine中出现的字母次数
        for (char magazineChar : magazine.toCharArray()) {
            ints[magazineChar - 'a']++;
        }
        //ransomNote出现的字母就进行-1
        for (char ransomNoteChar : ransomNote.toCharArray()) {
            ints[ransomNoteChar - 'a']--;

            //最后检查是否有字母次数小于0的，小于0则说明不够，返回false
            //在这里进行检查可以起到优化的作用
            if (ints[ransomNoteChar - 'a']<0){
                return false;
            }
        }

        return true;
    }
}

关于15. 三数之和：

题目描述：
● 给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。
● 注意： 答案中不可以包含重复的三元组。
● 示例：
● 给定数组 nums = [-1, 0, 1, 2, -1, -4]，
● 满足要求的三元组集合为： [ [-1, 0, 1], [-1, -1, 2] ]

该题的思路：
● 看到该题，之前做过两数之和和四数之和II的话，就会觉得用哈希法准没错，确实，该题用哈希法可以，但不值得，会很麻烦，因为题目说了要不重复，用哈希法的话，去重是个大问题。
● 那么该题使用什么解法呢，双指针！先将数组排序好，再根据两个指针的位置调整，从而不断逼近结果，直到两指针相遇。
● 因为该题有三个数，则先固定一个数i，让双指针进行调整位置即可，然后i进行遍历数组，将符合的加入结果集即可。
● 在遍历扫描的过程中，要特别注意去重操作，包括对a的去重，b和c的去重，需要好好理解。

代码实现

import java.util.ArrayList;
import java.util.List;
import java.util.Arrays;

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int left, right;
        List results = new ArrayList<>();

        Arrays.sort(nums);

        if (nums[0] > 0) {
            return results;
        }

        for (int i = 0; i < nums.length; i++) {
            //对a的去重
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            //下面这个方法会漏掉{-1，-1，2}这种类似的情况
            //if ((i + 1) < nums.length && nums[i] == nums[i + 1]) {
            //    continue;
            //}

            //left在i的后一个
            left = i + 1;
            //right指向最后一个元素
            right = nums.length - 1;

            //滑动循环判断
            while (left < right) {
                //求和 比较
                int sum = nums[i] + nums[left] + nums[right];

                if (sum > 0) {
                    right--;
                } else if (sum < 0) {
                    left++;
                } else {
                    //符合要求 加入结果集
                    results.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    //对left，即b去重
                    while (left < right && nums[left] == nums[left + 1]) {
                        left++;
                    }
                    //对right，即c去重
                    while (left < right && nums[right] == nums[right - 1]) {
                        right--;
                    }
                    left++;
                    right--;
                }

            }
        }

        return results;
    }
}

关于18. 四数之和

题目描述
● 题意：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。
● 注意：
● 答案中不可以包含重复的四元组。
● 示例： 给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。 满足要求的四元组集合为： [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]

该题的思路：
● 该题和上一题三数之和的操作95%相似，只是在三数之和的基础上多加了一层for循环，对于a,b,c,d四个数，我们可以先求出其中两个数的和的所有情况，然后把它看作三数之和的情况。
● 在三数之和中，是求a + b + c =0，而四数之和中是求 a + b + c + d=target，target是不确定的，故不能通过判断nums[i] > 0就进行剪枝返回了，若仍想进行剪枝操作，也可以，只需要nums[i] > 0 && nums[i] > target这样写即可，因为在保证当前nums[i]是正数的情况下，且nums[i] > target，则无论怎么组合四元组的值都是大于target的了。
● 注意：无论是在三数之和还是四数之和，都需要先将数组排序好再进行操作。
● 那么一样的道理，五数之和、六数之和等等都采用这种解法，指针法将时间复杂度：O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级。

代码实现：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {

        //要返回的结果集
        List results = new ArrayList<>();
        int left, right;

        //排序
        Arrays.sort(nums);

        //若小于4个长度，则无结果
        if (nums.length < 4) {
            return results;
        }
        //i，j为固定值
        for (int i = 0; i < nums.length; i++) {
            // nums[i] > target 直接返回, 剪枝操作
            if (nums[i] > 0 && nums[i] > target) {
                return results;
            }
            //对i去重
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            for (int j = i + 1; j < nums.length; j++) {
                //对j去重
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }

                left = j + 1;
                right = nums.length - 1;

                //循环滑动
                while (left < right) {
                    //求和 比较
                    long sum = (long) (nums[i] + nums[j] + nums[left] + nums[right]);
                    if (sum > target) {
                        right--;
                    } else if (sum < target) {
                        left++;
                    } else {
                        //加入结果集
                        results.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        //对left去重
                        while (left < right && nums[left] == nums[left + 1]) {
                            left++;
                        }
                        //对right去重
                        while (left < right && nums[right] == nums[right - 1]) {
                            right--;
                        }
                        left++;
                        right--;
                    }
                }
            }
        }

        return results;
    }
}

第六天结束，第七天加油！