基于时间序列的非周期预测模型
曹建文 1委兴宝 2,3 杨裔 2,4 李彩虹 2,3 赵文清 2,3
(1. 兰州工业学院计算机与人工智能学院,甘肃 兰州 730050; 2. 兰州大学信息科学与工程学院,甘肃 兰州 730000; 3. 旅游信息融合处理与数据权属保护文化和旅游部重点实验室,甘肃 兰州 730000; 4. 甘肃省人工智能与算力技术重点实验室,甘肃 兰州 730000 )
DOI:10.11959/j.issn.2096-0271.2025010
引用格式:
曹建文,委兴宝,杨裔;等.基于时间序列的非周期预测模型[J].大数据,2025,11(01):135-149.
CAO J W,WEI X B,YANG Y, et al.Model for non-periodic time series prediction[J].BIG DATA RESEARCH,2025,11(01):135-149.
摘 要 在实际应用中,纯周期性的数据相对罕见,大多数数据往往表现出非周期性特征,难以通过简单的周期性变化进行预测或描述。而单一神经网络在处理非周期性时间序列时往往面临过拟合、长时依赖捕获困难、非线性关系捕获有限等问题。为了有效地对非周期性时间序列进行预测,基于Informer模型提出了ILTNet模型。ILTNet模型结合线性预测(AR模型)和非线性预测(Informer模型与循环跳跃组件),能有效捕获长期依赖关系。实验证明,与LSTNet、Informer、AR以及GRU模型相比,ILTNet模型在非周期时间序列预测上表现出显著优势。例如,在Exchange Rate数据集上,ILNet模型相对于LSTNet模型,在步长为96和128时将RSE分别降低了0.0333和0.0277,相对于Informer模型在所有步长下,RSE均有显著降低,尤其是在步长为96时将RSE降低了0.2877。
关键词 多变量;时间序列预测;卷积神经网络;LSTNet;Informer
0 引言
通过分析丰富的历史时间序列数据,人们可以深入洞察未来发展趋势。根据实际需求,预测时间跨度可以划分为短期、中期和长期预测。其中,长期多变量时间序列预测具有重要的现实应用意义。它不仅有助于提前识别趋势变化,还能在变革到来之前提供采取应对措施的宝贵机会,从而在复杂多变的环境中保持竞争优势。这种方法不仅在经济领域具备显著价值,还被广泛应用于交通、光能、气象学等众多领域。笔者将进一步探讨这一关键方法的实际应用和潜在影响,为决策者和研究者提供宝贵的见解。
多变量时间序列预测方式目前主要被分为3类:统计模型、机器学习模型以及深度神经网络。其中自回归模型(autoregressive model,AR模型)与自回归移动平均模型(autoregressive integrated moving average model,ARIMA)是两个被广泛使用的统计模型。自回归模型用同一变量历史的表现情况来预测该变量未来的表现情况,并假设它们为线性关系,而ARIMA将时间序列建模为历史数据和白噪声的线性组合,但这些模型只能应用于内部具备线性关系的序列,并且其并没有考虑变量之间的依赖关系,所以在很多实际应用中不能使用。机器学习模型如支持向量机(support vector machines,SVM)、随机森林(random forest,RF)、极端梯度提升(extreme gradient boosting,XGBoost)等,以数据驱动的方式学习序列的特征,建模历史数据和未来数据之间的映射关系,虽然适用范围更广,精度也有所提升,但是特征选择往往非常耗时。近年来,神经网络能够提取非线性关系,能够从输入信号中学习复杂的模式等特性,以神经网络为代表的深度学习算法成为预测领域的研究热点。在研究将深度神经网络应用于时间序列预测时,尽管这些模型通常表现优异,但它们在处理非周期性时间序列方面存在一些问题。例如,卷积神经网络(convolution neural network,CNN)和递归神经网络(recurrent neural network,RNN)在提取特征和处理时间依赖性方面表现出色,但在处理非周期性模式时往往表现较差。其他混合模型如TCN-Linear(temporal convolutional network - linear)尝试通过结合时间卷积网络和线性组件来增强在混沌时间序列上的表现,但即便是这些先进的模型,在处理非周期性场景时也有其局限性。另外,Lai等提出了一种新的深度学习框架,通过CNN提取短期特征和RNN中的门控循环单元(gated recurrent unit,GRU)学习时间依赖性,引入线性分量AR模型,简单地组合起来就能得到很好的预测效果,但是在非周期模式上表现较差。多变量时间序列数据集的预测误差很大程度上取决于元数据集的时间周期模式和相互依赖性,通常采用各种隐式或显式的方法提取多变量时间序列之间的相互依赖关系。Zhou等在Transformer模型的基础上提出了一种优化模型Informer模型,继承了Transformer模型的Self-Attention机制与编码器译码器构造,并引入ProbSparse Self-Attention机制,提升了预测精确度,同时有效降低了计算复杂度,它的编码器和译码器都是一系列循环神经网络,输入序列和输出序列的长度可以不同。尽管Informer模型能够有效地实现长距离时间序列预测,但在非周期性时间序列预测方面仍存在不足,这导致其在某些实际应用中的预测精度相对较低,需要进一步改进。
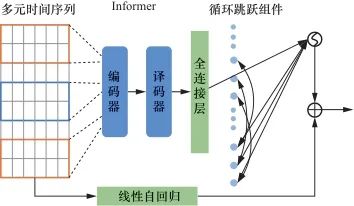
为了实现多变量长距离预测,并解决Informer模型对于非周期序列预测精度不足的问题,提出了一种基于Informer的长期时间序列网络(Informer long-term time-series network,ILTNet)模型。该模型使用没有池化层的卷积神经网络提取时间维度上的短期模式以及变量间的局部依赖关系,基于编译码结构捕捉长期依赖的优势,结合循环跳跃组件准确捕捉时序数据中蕴藏的周期性,使用线性自回归模型提取时间序列数据的线性趋势,最后并行输出。该模型在周期的电能数据集以及非周期的汇率数据集上进行了验证。
1 模型构建与相关理论
在实际应用中,时间序列数据呈现出多样的特征,有些具有明显的周期性,而有些则表现为非周期性。模型构建的过程中,为了更好地应对这种多样性,将预测任务分解为周期性预测任务和非周期性预测任务。循环跳跃组件预测周期性部分,自回归模型和Informer模型分别预测非周期性的线性部分和非线性部分。模型预测窗口的大小固定,使用滚动预测,在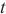 时刻输入数据
时刻输入数据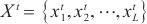 ,其中
,其中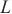 为输入长度。先用卷积神经网络进行卷积,再使用编译码结构和循环跳跃组件捕捉长期依赖关系,将该非线性神经网络部分与自回归线性模型并行,使模型对时间序列具有更强的鲁棒性,输出
为输入长度。先用卷积神经网络进行卷积,再使用编译码结构和循环跳跃组件捕捉长期依赖关系,将该非线性神经网络部分与自回归线性模型并行,使模型对时间序列具有更强的鲁棒性,输出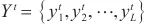 ,
,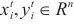 ,
,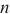 为变量维度,为了预测
为变量维度,为了预测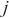 时刻后
时刻后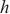 时间的
时间的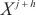 ,假设
,假设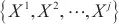 是已知的。模型总体构建情况如图1所示。
是已知的。模型总体构建情况如图1所示。
1.1 Informer模型
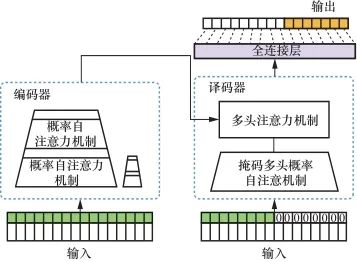
对于非周期性的变化,传统的神经网络很难进行精确预测。为了有效捕获输出和输入之间精确的长期依赖关系,从而使模型拥有优秀的预测能力,可使用Informer模型机制。Informer模型采用Transformer模型的编码译码结构,使用自注意力蒸馏机制,提取主要注意力,大幅降低了网络的规模,并引入概率注意机制来预测长序列,有效地降低了运算量,缩短了运行时间。
传统的Transformer模型计算Self-Attention值的方法是根据输入信息Q(query)、键K(key)和值V(value),将Q和每个K进行相似度计算得到权重,通常使用相似度函数,例如点积、拼接、感知机等,再使用一个Softmax函数对这些权重进行归一化,最后将权重和相应的键值进行加权求和得到最后的Attention,计算式可表述为式(1),其中d是输入的维数。
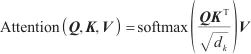 | (1) |
第i个信息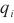 的注意力概率形式如下。
的注意力概率形式如下。
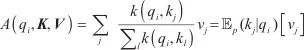 | (2) |
原自注意力机制存在稀疏性,较少的点积贡献了绝大部分的注意力得分,其余部分贡献极小,可以忽略不计。利用KL散度(Kullback-Leibler divergence)区分稀疏性,其中第i个query的稀疏性评估方法可由下述计算式计算得到。
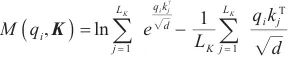 | (3) |
ProbSparse自注意力计算式如(4)所示,它只包含稀疏测度M(w, K)下的主要u信息,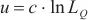 ,c为常数采样因子,每个头产生不同的稀疏查询键对,避免了严重的信息损失。
,c为常数采样因子,每个头产生不同的稀疏查询键对,避免了严重的信息损失。
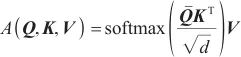 | (4) |
其中,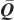 与
与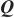 是大小相同的稀疏矩阵。
是大小相同的稀疏矩阵。
Informer模型中的稀疏注意力机制通过选择性地关注少数关键位置,将计算复杂度和内存使用量降低到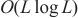 ,从而显著提高计算和内存效率,减少冗余计算,增强模型的可扩展性,并有效捕捉长程依赖关系和保留全局信息,使模型能够高效处理长序列数据,并保持对整体数据模式的理解。
,从而显著提高计算和内存效率,减少冗余计算,增强模型的可扩展性,并有效捕捉长程依赖关系和保留全局信息,使模型能够高效处理长序列数据,并保持对整体数据模式的理解。
另外,Informer模型的编码器允许处理更长的序列输入,捕获长序列输入之间的鲁棒的远距离依赖关系。由于ProbSparse自注意机制特征映射会存在值的冗余组合,因此,这里利用蒸馏操作对具有优势特征赋予更高权重,并在下一层生成有重点的自我注意力的特征映射。从i到i+1层的蒸馏操作的过程如下。
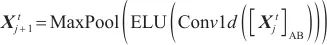 | (5) |
其中,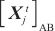 代表注意力块。使用ELU激活函数在时间序列上执行一维卷积。在堆叠一层后,在其半片中加入最大池化层和下采样
代表注意力块。使用ELU激活函数在时间序列上执行一维卷积。在堆叠一层后,在其半片中加入最大池化层和下采样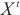 ,从而降低整个内存使用量。为了增强蒸馏操作的鲁棒性,用一半的输入构建主堆栈的副本,并通过每次减少一层来逐步减少自注意蒸馏层的数量,这样它们的输出维数是对齐的。将所有堆栈的输出连接起来,得到编码器的最终隐藏表示。
,从而降低整个内存使用量。为了增强蒸馏操作的鲁棒性,用一半的输入构建主堆栈的副本,并通过每次减少一层来逐步减少自注意蒸馏层的数量,这样它们的输出维数是对齐的。将所有堆栈的输出连接起来,得到编码器的最终隐藏表示。
Informer模型的译码器在一次前向计算过程中,能够预测长序列的输出,该模型由多头注意力层和掩码多头概率自注意力层组成,在计算过程中,采用迭代式预测策略,输出多步长预测结果。
在译码器中,在第一层译码器输入时将序列长度遮蔽一半,大大减小了译码器内存开销,缩短了计算时间,在t时刻输入数据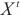 变换为矩阵,也就是式(6)同时提出在译码结构中使用生成式结构,能够一次生成全部预测序列,缩短了预测译码耗时,加快推理速度。
变换为矩阵,也就是式(6)同时提出在译码结构中使用生成式结构,能够一次生成全部预测序列,缩短了预测译码耗时,加快推理速度。
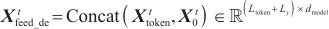 | (6) |
其中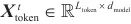 是起始字符,
是起始字符,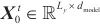 是目标序列的占位符,可以将标量设置为0。通过将被屏蔽的点积设置为-∞,防止每个位置都参与到下一位置,避免了自回归,最终输出如下。
是目标序列的占位符,可以将标量设置为0。通过将被屏蔽的点积设置为-∞,防止每个位置都参与到下一位置,避免了自回归,最终输出如下。
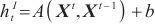 | (7) |
Informer的模型结构如图2所示。
1.2 循环跳跃组件
对于周期的数据,时序性的循环神经网络是一种很好的处理方式,但是对于周期较长的数据,现有的循环神经网络很难被捕捉,会产生梯度消失的问题。为了捕捉数据中的长期相关性,使用一个带有时间跳跃连接的GRU循环神经网络,这个SKIP组件就是在相邻周期的当前隐藏单元格和同一阶段的隐藏单元格之间添加跳转连接,延长数据的时间跨度,避免了可能出现的梯度消失问题。
长短期记忆(long short-term memory,LSTM)网络是在传统的循环神经网络上引入了门结构,使用输入门、遗忘门和输出门分别控制输入值、记忆值和输出值,可以解决长期依赖问题,而GRU在保留了LSTM网络的特性后,进行了进一步的简化,直接把某一时刻的长期记忆作为输出,只有更新门和重置门两种门操作,减少了运算量。GRU在t时刻前向传播计算的过程如下。
重置门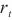 ,根据当前输出需要用到的记忆部分如下。
,根据当前输出需要用到的记忆部分如下。
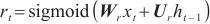 | (8) |
更新门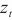 ,表示以前的信息是否需要更新。
,表示以前的信息是否需要更新。
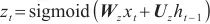 | (9) |
候选输出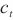 ,t时刻加入新信息,用
,t时刻加入新信息,用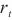 来控制需要保留多少信息。
来控制需要保留多少信息。
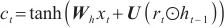 | (10) |
在t时刻,忘记传递下来的t-1时刻中的某些维度信息,并加入当前节点输入的某些维度信息,最终输出如下。
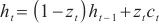 | (11) |
其中,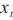 为t时刻的输入,W是与当前输入
为t时刻的输入,W是与当前输入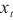 相关的权重矩阵,U是与前一时刻隐藏状态
相关的权重矩阵,U是与前一时刻隐藏状态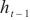 相关的权重矩阵,☉表示矩阵点乘。
相关的权重矩阵,☉表示矩阵点乘。
使用RELU函数作为隐藏层的更新激活函数。加入跳转连接后,整个循环跳跃更新如下。
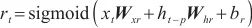 | (12) |
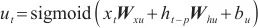 | (13) |
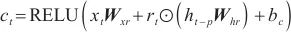 | (14) |
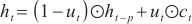 | (15) |
其中,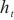 表示在t时刻的循环分量的隐藏状态,p是跳过的隐藏单元数,p值可根据数据集明显的周期确定,能显著地提高模型的性能。t时刻的循环跳跃层输出为
表示在t时刻的循环分量的隐藏状态,p是跳过的隐藏单元数,p值可根据数据集明显的周期确定,能显著地提高模型的性能。t时刻的循环跳跃层输出为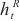 ,从时间t-p+1到t时循环跳跃组件跳过量为p,可用
,从时间t-p+1到t时循环跳跃组件跳过量为p,可用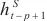 ,
,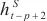 ,…,
,…,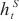 表示,全连接层输出式如下。
表示,全连接层输出式如下。
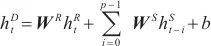 | (16) |
1.3 自回归组件
Informer模型部件主要处理非周期性非线性部分,导致对线性部分的预测准确度下降。而线性模型对输入数据的线性变化非常敏感,因此选择使用AR模型来处理线性分量。AR模型的时间序列中存在线性关系,它使用之前的观察值作为回归方程的输入,以预测下一个时间步的值。
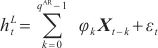 | (17) |
其中,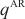 为输入矩阵上窗口的大小,
为输入矩阵上窗口的大小,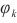 为自相关系数,
为自相关系数,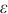 为随机误差项,均值为0,标准差为δ。由以上计算式可知,自回归模型具有简单、易解释、计算效率高和擅长捕捉线性依赖关系的优势。
为随机误差项,均值为0,标准差为δ。由以上计算式可知,自回归模型具有简单、易解释、计算效率高和擅长捕捉线性依赖关系的优势。
神经网络最终的预测结果是将周期部分和非周期部分的输出分量进行积分。t时刻的最终预测方法如式(18)所示。
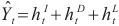 | (18) |
其中,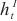 是Informer模型的输出,
是Informer模型的输出,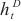 是循环跳跃组件处理后的输出,其计算如前文所述。
是循环跳跃组件处理后的输出,其计算如前文所述。
1.4 实验设计
基于所构建的混合模型,预测模型的实验流程如图3所示。首先,通过规范化周期性特征和填补缺失值对数据进行标准化处理,同时计算相关系数以筛选有用特征,从而去除冗余信息并确保数据的质量。其次,使用滑动窗口机制构建时间序列样本,通过选择不同的步长构建多种样本,旨在捕捉时间序列中的短期和长期依赖关系。之后,在模型训练阶段,将构建的时间序列样本输入提出的ILTNet模型中进行训练。最后,采用相对绝对误差(relative absolute error,RAE)、相对平方误差(relative squared error,RSE)等评估指标对模型进行评估,并比较不同模型(如ILTNet、LSTNet、Informer、AR、GRU模型等)的预测结果。这种方法可以确定最优模型,并全面评估其性能表现。
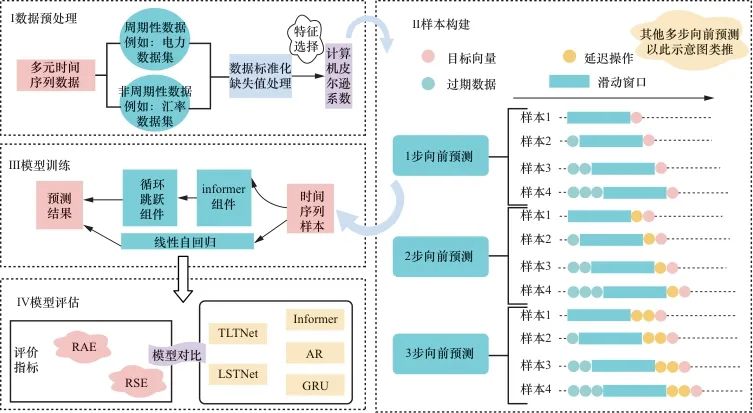
选择LSTNet、Informer、AR和GRU模型作为对比模型的原因主要有两个。首先,ILTNet模型的设计集成了LSTNet、Informer、AR和GRU模型的关键特性和优势。选择这些模型作为对比,可以直观地展示ILTNet模型相对于其组成部分的创新和性能提升。例如,ILTNet模型的线性预测部分基于AR模型,而非线性预测部分则融合了Informer和GRU模型的优势。这种对比不仅突出了ILTNet模型的综合能力,还验证了其在长期依赖捕获、周期性特征处理和综合预测能力方面的改进效果。
上述4种模型在时间序列预测领域具有代表性和广泛应用性。LSTNet模型结合了CNN和LSTM网络,在处理长期依赖和周期性特征数据方面表现出色。Informer模型以其稀疏注意力机制和高效处理长序列的能力著称,特别适用于大规模数据和长序列预测。AR模型作为传统的线性时间序列模型,以其简单性和高效性在处理线性关系时具有重要参考价值。GRU模型则通过其门控机制有效捕获时间序列中的依赖关系,特别适合非线性时间序列预测。选择这些模型作为对比基础,能够全面评估ILTNet模型在不同预测方法和策略下的性能,展示其相对于基础模型的优势和改进。
除了以上对比实验,为了保证对基于时间序列的周期性预测和非周期性预测的有效性,本文选择了两个具有不同时间分辨率和特征的数据集——Electricity数据集(高频电力消费数据)和Exchange Rate数据集(低频汇率数据)。这两个数据集涵盖了周期性和非周期性的时间序列,分别代表了具有明显周期性特征的电力消耗和相对平稳的汇率变动,从而能够有效测试模型在不同时间序列特征下的预测能力。
1.5 模型复杂度分析
ILTNet模型融合了Informer模型的稀疏注意力机制、GRU模型的非线性处理能力以及AR模型的线性预测能力,这种综合设计虽然提升了模型的预测性能,但也增加了模型的复杂度。由于ILTNet模型结合了多种机制,模型的参数量较单一的Informer、GRU或AR模型要多,从而导致训练和推理过程中的计算开销增加。具体而言,ILTNet模型的时间复杂度为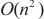 (注意力机制)加上
(注意力机制)加上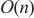 (循环神经网络),其中
(循环神经网络),其中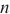 是时间序列的长度,这意味着随着数据量和序列长度的增加,计算开销也会显著提高。
是时间序列的长度,这意味着随着数据量和序列长度的增加,计算开销也会显著提高。
在训练过程中,由于ILTNet模型结构复杂、参数量大,其训练时间较长,特别是在处理大规模数据集时非常明显。为突破大规模数据集的计算瓶颈,可能需要采用分布式计算或高性能计算资源来加速训练和推理。虽然ILTNet模型设计具备一定的可扩展性,通过调整网络层数或参数量可在一定程度上提高对大规模数据的适应能力,但这可能会影响模型的预测性能。因此,在实际应用中,需要在模型复杂度与预测精度之间找到平衡,同时考虑使用简化版模型或优化算法来提升效率。
2 实验与分析
2.1 实验环境
本文基于Pytorch框架进行实验。Pytorch是一个Python优先的深度学习框架,所用库的版本号如下:Python 3.7.3;matplotlib 3.1.1;numpy 1.16.4;pandas 0.24.2;scikit_learn 0.21.2;torch == 1.10.0。
2.2 数据集描述
笔者使用了两个公开的数据集,第一个是UCI机器学习与智能系统中心中的Electricity数据集:2012—2014年,每15 min记录一次千瓦时用电量,一天呈现96个小节,所有时间点的凌晨1:00和2:00之间均为零,时间序列的长度为26 304,包含321个变量。第二个是Exchange Rate数据集,包括澳大利亚、英国、加拿大、瑞士、中国、日本、新西兰、新加坡8个国家从1990年到2016年的每日汇率汇总,时间序列的长度为7 588,包含8个变量。这两个数据集代表了两种不同的非周期性时间序列。一个是基于电力消费的高频数据,另一个是基于汇率的低频数据。它们涵盖了不同的时间分辨率和变量类型,能够较好地代表可能的非周期性时间序列。
对两个不同类型的数据集,使用皮尔逊相关系数计算序列之间的特征相关性生成热力图,如图4、图5所示。
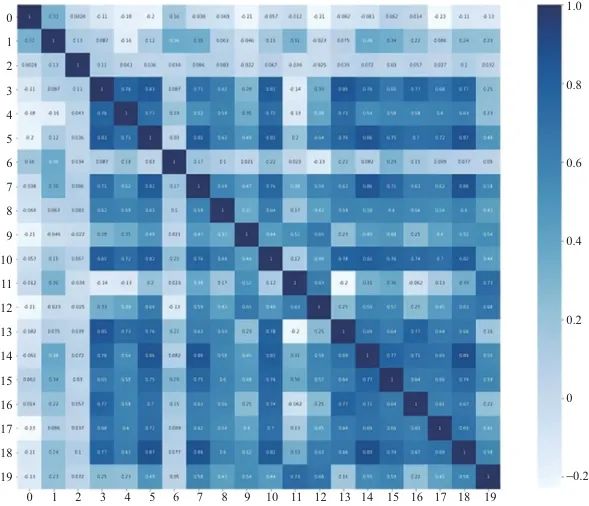
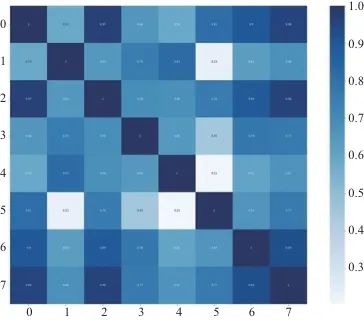
2.3 对比实验和参数设置
为了进一步验证ILTNet模型的预测能力,从数据集的选取上考虑到数据集的周期性,Electricity数据集具有一定的周期性,而Exchange Rate数据集具有非周期性。ILTNet模型超参数进行网格搜索,采用Adam优化器进行优化。对比实验选用了以下4种对比模型,参数使用的是默认推荐参数。
(1)LSTNet模型
其是一个多变量深度序列预测模型,使用CNN和RNN来提取变量之间的短期局部依赖模式,并发现时间序列趋势的长期模式,利用传统的自回归模型提取时间序列中的线性关系。
(2)Informer模型
该模型是一种专为长序列时间序列预测设计的、基于注意力机制的编码器/译码器构造模型,解决了Transformer模型在应用于长序列时间序列预测时存在的一些严重的问题,如二次时间复杂度较高、较高的内存使用量和编译码器结构的固有限制等。
(3)AR模型
AR模型是一个基本的单变量时间序列建模、预测模型,是简单且具代表性的随机过程,其将当前时刻的输出变量当作历史时间段变量的线性加权和。
(4)GRU模型
GRU模型是LSTM网络的一种效果很好的变体,它较LSTM网络的结构更加简单,而且可以更好地解决长依赖问题。
2.4 评价指标
笔者使用了以下两种常用的指标来评价模型预测的效果。
(1)相对平方根误差
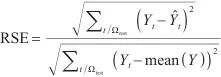 | (19) |
(2)相对绝对值误差
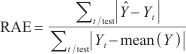 | (20) |
其中,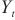 、
、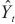 分别代表
分别代表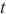 时刻的真实值、预测值,
时刻的真实值、预测值,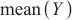 代表实际值的平均值。相对平方根误差和相对绝对值误差越小表示模型越优。
代表实际值的平均值。相对平方根误差和相对绝对值误差越小表示模型越优。
RSE和RAE是时间序列预测领域中被广泛使用的两个指标。RSE衡量了预测值相对于真实值的平方误差在整个时间序列中的占比,而RAE则评估了预测误差的绝对值相对于真实值的平均值的比重。由于这两个指标能够直接反映模型的预测精度和误差分布,且在许多研究中被证明是有效和可靠的,因此常被用来评估预测模型的性能。
2.5 实验结果
5个模型在两个数据集上的预测结果见表1,每个数据指标对应的最好的结果用黑体突出显示。时间长度分别为96、128、168、196,代表96小时、128小时、168小时、196小时的电力预测,以及96天、128天、168天、196天的汇率数据。一般时间长度越大,预测任务就越困难。用RSE度量时,ILTNet模型均优于其他4个模型;用RAE度量时,ILTNet模型仍然具有一定的优势,尤其是在非周期的Exchange Rate数据集上也能表现出良好的预测情况。整体来说,ILTNet模型在多变量预测任务中可以获得较高的整体预测精度。
表1 多变量时序预测实验对比结果
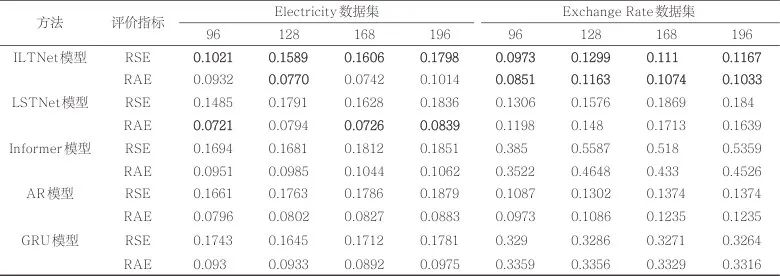
在Electricity数据集上,ILTNet模型相较于LSTNet模型,在不同步长下的性能表现如下。
 当步长为96时,RSE降低了0.0464,但RAE增加了0.0211。
当步长为96时,RSE降低了0.0464,但RAE增加了0.0211。
 当步长为128时,RSE降低了0.0202,RAE降低了0.0024。
当步长为128时,RSE降低了0.0202,RAE降低了0.0024。
 当步长为168时,RSE降低了0.0022,但RAE增加了0.0016。
当步长为168时,RSE降低了0.0022,但RAE增加了0.0016。
 当步长为196时,RSE降低了0.0038,但RAE增加了0.0175。
当步长为196时,RSE降低了0.0038,但RAE增加了0.0175。
相比于Informer模型,ILTNet模型在以下方面表现出显著改进。
 步长为96时,RSE降低了0.0673,RAE降低了0.0019。
步长为96时,RSE降低了0.0673,RAE降低了0.0019。
 步长为128时,RSE降低了0.0092,RAE降低了0.0215。
步长为128时,RSE降低了0.0092,RAE降低了0.0215。
 步长为168时,RSE降低了0.0206,RAE降低了0.0302。
步长为168时,RSE降低了0.0206,RAE降低了0.0302。
 步长为196时,RSE降低了0.0053,RAE降低了0.0048。
步长为196时,RSE降低了0.0053,RAE降低了0.0048。
综上所述,在周期数据集上,ILTNet模型相较于Informer模型在RSE和RAE误差方面均有显著降低,而与LSTNet模型相比,虽然在部分步长下RAE略有增加,但总体上RSE表现更优。
在Exchange rate数据集上,ILTNet模型表现出相对于LSTNet和Informer模型的显著优势。与LSTNet模型相比,ILTNet模型在步长为96和128时分别将RSE降低了0.0333和0.0277,同时将RAE降低了0.0347和0.0317。然而,在步长为168时,ILTNet的RSE和RAE分别增加了0.0759和0.0639。在步长为196时,RSE和RAE分别降低了0.0673和0.0606。相较于Informer模型,ILTNet模型在所有步长下均表现出显著的改进。
总的来看,在非周期性数据集上,ILTNet模型的表现全面优于对比的LSTNet模型和Informer模型,展示了其在处理不同步长数据时的稳健性和准确性。
在实验中选择不同步长(如96、128、168、196小时或天)进行预测是为了全面评估模型在不同时间尺度下的表现。较短的步长能够更有效地捕捉短期模式和趋势,而较长的步长则有助于评估模型在处理长期趋势和复杂依赖关系方面的能力。鉴于重点是评估模型的长期预测能力,因此最小步长设置为96小时。实验结果表明,对于两个数据集,随着步长的增加,各模型的RSE和RAE值普遍上升,预测精度逐渐降低。这一现象可以归因于较长步长下预测任务的复杂性增加,使模型在捕捉长期依赖和趋势时面临更多挑战。
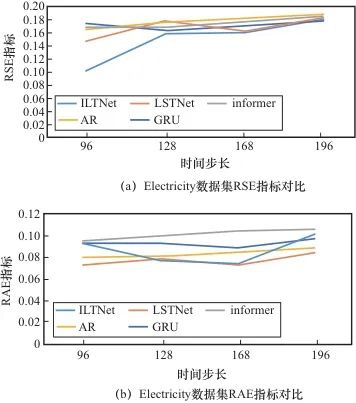
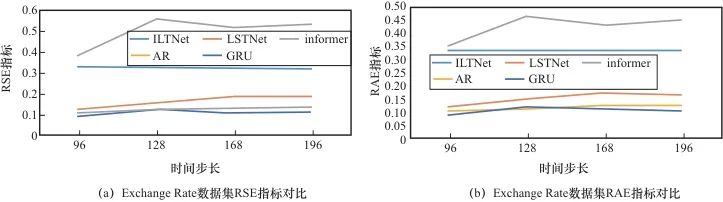
为了直观地将本文算法和其他算法进行对比,笔者将数据进行了可视化。Electricity数据集的相对平方根误差和相对绝对值误差对比如图6所示。在RSE上,ILTNet模型效果优于其他4个模型,但是在RAE上,ILTNet模型整体效果略低于LSNet模型和AR模型,这是因为Electricity数据集具有较强的周期性,线性关系明显,随着模型复杂度的提升,使用ILTNet模型反而增加了冗余层的参数学习。Exchange Rate数据集的相对平方根误差和相对绝对值误差对比如图7所示,在RSE和RAE上,ILTNet模型都优于其他4个算法。对于周期性不明显的时间序列,ILTNet模型能敏锐地捕捉到长期依赖关系,以及提取到主要特征。
使用ILTNet模型在Electricity数据集和Exchange Rate数据集上进行预测,如图8所示,预测的时间序列(蓝色)和数据集上的真实数据(黄色)对比,ILTNet模型能较好地拟合出数据的趋势。
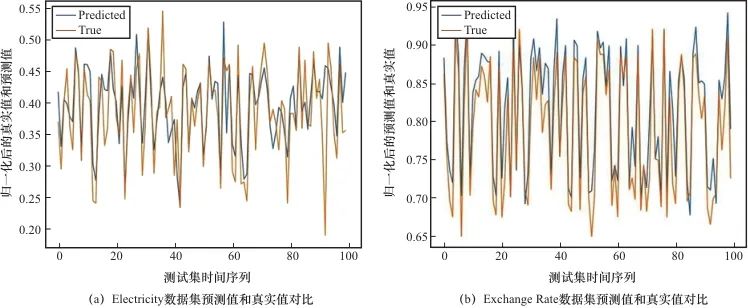
具体而言,ILTNet模型在不同数据集上的优越表现主要归因于其综合模型设计。该模型有效融合了Informer模型的稀疏注意力机制、跳接记忆循环神经网络的非线性处理能力与自回归模型的线性预测能力。这种综合设计形成了一个高效的预测框架,使模型能够充分发挥各组件的优势,从而显著提升了对复杂时间依赖关系数据的整体预测性能。
此外,周期性与非周期性特征优化也是ILTNet模型优越表现的重要因素。在周期性数据集(如Electricity数据集)上,ILTNet模型通过增强对周期性特征的捕捉能力,显著降低了相对平方根误差。尽管在某些步长下,相对绝对值误差存在一定波动,但整体性能仍优于其他对比模型。在非周期性数据集,如Exchange Rate数据集上,ILTNet展示了卓越的鲁棒性和准确性,尤其在较长时间步长下,能够有效降低RSE和RAE,证明了其在长期依赖关系捕捉方面的显著优势。综合来看,ILTNet模型在多变量时间序列预测任务中的表现优异,得益于其综合性的模型设计和对不同数据特征的优化能力。
然而,实验结果可能受到数据集特性影响。Electricity数据集具有显著的周期性特征,其高频电力消耗数据展现出明显的周期性模式。这一特性使周期性数据的预测任务相对复杂,但也使ILTNet模型在捕捉这些周期性特征时表现优异。尽管在某些步长下相对绝对值误差有所波动,但整体的相对平方根误差依然较低,表明ILTNet模型能够有效处理周期性特征并进行准确预测。
相对而言,Exchange Rate数据集具有平稳的非周期性特征,该低频汇率数据的波动较少,主要受长期趋势和随机变量的影响。ILTNet模型在处理这种非周期性数据时展现出卓越的鲁棒性,特别是在较长时间步长下有效降低了RSE和RAE,显示了其在捕捉长期依赖关系和复杂非周期性特征方面的显著优势。
因此,数据集特性对实验结果产生了显著影响。Electricity数据集的周期性特征和Exchange Rate数据集的非周期性特征分别对模型的预测能力提出了不同的挑战。ILTNet模型在这两种数据集上的优异表现证明了其在处理不同时间序列数据时的适应性和有效性。
3 结束语
针对多变量时间序列长期预测的不足之处,本文提出了一种基于Informer模型、跳接记忆循环神经网络以及自回归模型的ILTNet模型。在Electricity数据集和Exchange Rate数据集上,将ILTNet模型同LSTNet、Informer、AR以及GRU模型进行对比,在对比实验中均优于其他模型。对比单个模型,证明了将LSTNet模型与Informer模型有效结合,可以提升模型的性能。当预测长度增大时,模型的性能有所下降,这是长期时间序列预测很难避免的一个问题,为了提升模型的预测性能,下一步将考虑优化特征选择。此外,深度学习方法在对时间序列预测时,未充分考虑空间依赖性,未来可以考虑时域卷积网络(temporal convolutional network,TCN)提取时域特征,TCN的卷积内核可以在一个层中共享,降低模型的使用内存,以改进当前算法,获得更佳的预测效果。此外,还需增加更多具有代表性的数据集,涵盖不同领域和时间尺度的非周期性时间序列,以全面验证所提模型的泛化能力和鲁棒性。
作者简介
曹建文,男,兰州工业学院计算机与人工智能学院副教授,主要研究方向为计算机技术。
委兴宝,女,兰州大学信息科学与工程学院硕士生,主要研究方向为时间序列分析、人工智能。
杨裔,男,博士,兰州大学信息科学与工程学院教授,主要研究方向为大数据分析、机器学习、人工智能。
李彩虹,女,博士,兰州大学信息科学与工程学院教授级高级实验师,主要研究方向为计算机科学与技术。
赵文清,女,兰州大学信息科学与工程学院硕士生,主要研究方向为旅游情感分析与人工智能。
联系我们:
Tel:010-53879208
010-53859533
E-mail:bdr@bjxintong.com.cn
http://www.j-bigdataresearch.com.cn/
转载、合作:010-53878078
大数据期刊
《大数据(Big Data Research,BDR)》双月刊是由中华人民共和国工业和信息化部主管,人民邮电出版社主办,中国计算机学会大数据专家委员会学术指导,北京信通传媒有限责任公司出版的期刊,已成功入选中国科技核心期刊、中国计算机学会会刊、中国计算机学会推荐中文科技期刊,以及信息通信领域高质量科技期刊分级目录、计算领域高质量科技期刊分级目录,并多次被评为国家哲学社会科学文献中心学术期刊数据库“综合性人文社会科学”学科最受欢迎期刊。

关注《大数据》期刊微信公众号,获取更多内容
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








