相机参数标定

一、相机标定原理

1.1 切向畸变与径向畸变

相机标定是标定图像产生的畸变，畸变的类型主要有一下三种：

①径向畸变是由透镜本身的制造误差造成的

②切向畸变是由于透镜安装与“图像”平面不平行产生的

③焦距和主点（焦距影响图像的模糊程度，主点影响位置的偏移）

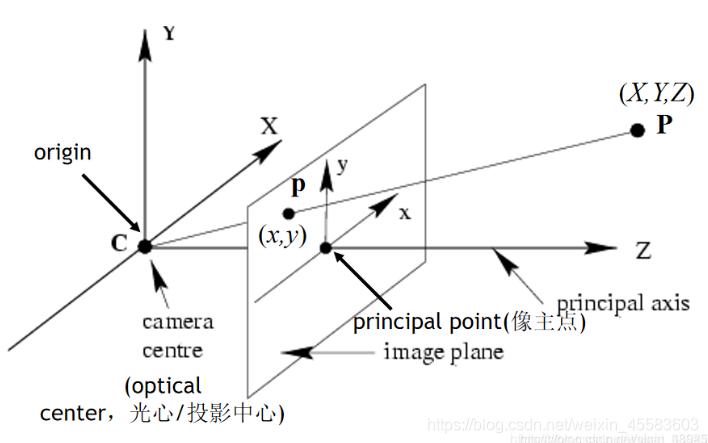
下图为小孔成像模型

1.2 张氏标定法

”张正友标定法” 是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点。相对于自标定而言，提高了精度，便于操作。因此张正友标定法被广泛应用于计算机视觉方面。
算法描述：
1、打印一张模板并贴在一个平面上；
2、从不同角度拍摄若干张模板图像；
3、检测出图像中的特征点；
4、求出摄像机的内参数和外参数；
5、求出畸变系数；
6、优化求精。

1.3 步骤

1、计算单应性矩阵H
单应性：在计算机视觉中被定义为一个平面到另一个平面的投影映射。首先确定，图像平面与标定物棋盘格平面的单应性。
设三维世界坐标的点为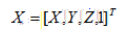 ，二维相机平面像素坐标为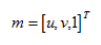，所以标定用的棋盘格平面到图像平面的单应性关系为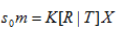： (其中，K为相机的内参矩阵，R为外部参数矩，K为相机的内参矩阵，R为外部参数矩阵（旋转矩阵），T为平移向量。令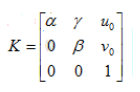，设棋盘格位于Z=0的平面，定义旋转矩阵R的第i列为 ri, 则有：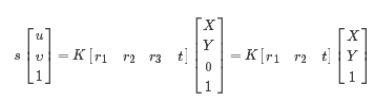
于是空间到图像的映射可改为：H=λK[r1 r2 t]
其中H 是描述Homographic矩阵,可通过最小二乘，从角点世界坐标到图像坐标的关系求解。

2、计算内参数矩阵
根据步骤1中的式子，令 H 为 H = [h1 h2 h3]，则 [h1 h2 h3]=λK[r1 r2 t]，再根据正交和归一化的约束可以得到等式：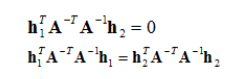
即每个单应性矩阵能提供两个方程，而内参数矩阵包含5个参数，要求解，至少需要3个单应性矩阵。为了得到三个不同的单应性矩阵，我们使用至少三幅棋盘格平面的图片进行标定。通过改变相机与标定板之间的相对位置来得到三个不同的图片。为了方便计算，我们定义：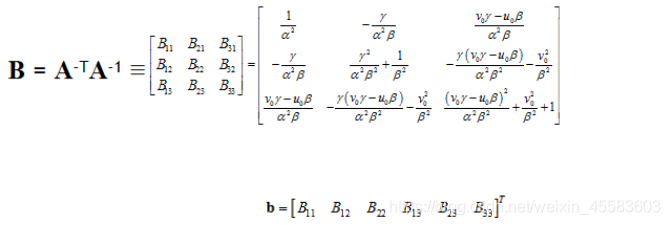
B 中的未知量可表示为6D 向量 b，

设H中的第i列为 hi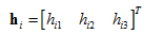，，根据b的定义，可以推导出公式，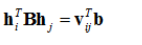
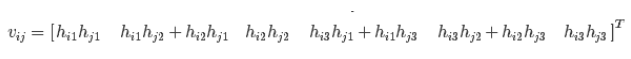，最后推导出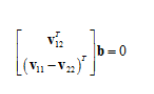
通过上式，我们可知当观测平面 n ≥ 3 时，即至少3幅棋盘格图像，可以得到b的唯一解，求得相机内参数矩阵K。

3、计算外参数矩阵
外部参数可通过Homography求解，由 H = [h1 h2 h3] = λA[r1 r2 t]，可推出

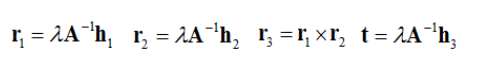
4、最大似然估计

上述的推导结果是基于理想情况下而言，但由于可能存在一些其他干扰，所以使用最大似然估计进行优化。假设拍摄了n张棋盘格图像，每张图像有m个角点。最终获得的最大似然估计公式为

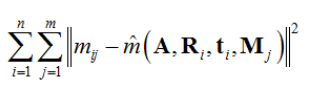
二、实验

2.1棋盘环境

运行环境：pyhton2.7、pycharm编译器
测试条件：手机拍照（图像16张）、手机型号iphonex

2.2 实验数据集

2.3 实现代码

import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((4 * 6, 3), np.float32)
objp[:, :2] = np.mgrid[0:6, 0:4].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("C:/qipan/*.png")
i=0;
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (6, 4), None)
    #print(corners)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (6, 4), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        i+=1;
        cv2.imwrite('conimg'+str(i)+'.jpg', img)
        cv2.waitKey(1500)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")

img = cv2.imread(images[2])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片（正常重映射之后会删掉一部分图像）
print (newcameramtx)
print("------------------使用undistort函数-------------------")
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibresult3.jpg', dst1)
print("方法一:dst的大小为:", dst1.shape)

2.4 实验结果

2.4.1 内参结果

由结果可得iphonex后置摄像头的参数矩阵为：

2.4.2 外参结果

1、旋转向量

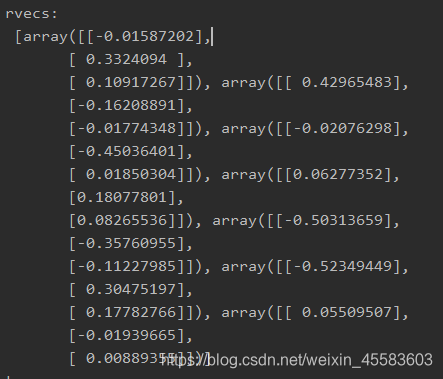
2、平移向量

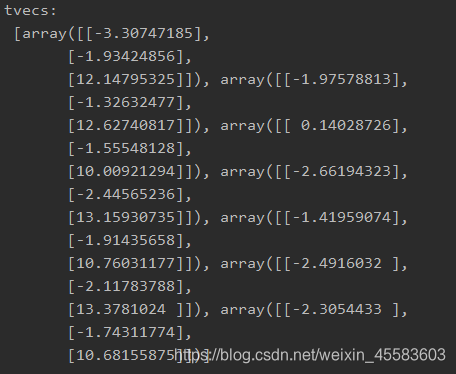
三、实验小结

1、通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差。
2、
由上图结果可看出，焦距fx=2.11,及fy=2.05（约等于）。
3、intrinsics_parm为内参，一个相机只有一个内参，distortionk为畸变系数K，extrinsics_parm为外参数，因为拍摄角度的不同所以每一张的外参也不相同，有12张图片就有12个外参。
4、在这里，要注意的是所使用的图片要先转为灰度图再运行，因为原图所占空间较大怕影响处理速度，而且图片若是不经过比例压缩会导致图像变形，方格就没那么精确，结果也会有较大的偏差。