240.搜索二维矩阵

题目：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

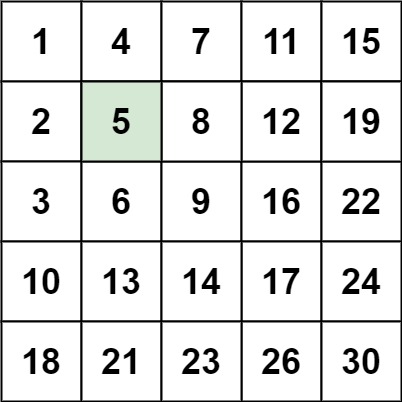
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

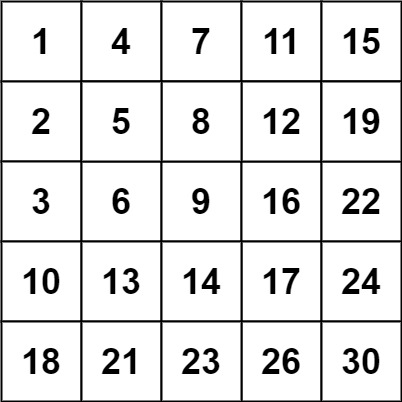
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -109 <= target <= 109

解题思路：

判断每行的第一个元素是否比target大如果大后续所有元素都不需要比较了，因为每行的第一个元素是当前行及下边所有行中最小值。然后判断每列的元素，如果当前列元素比target大则直接跳过后续元素

代码：

class Solution:
    def searchMatrix(self, matrix, target: int) -> bool:
        for i in range(len(matrix)):
            if matrix[i][0]>target:
                return False
            for j in range(len(matrix[0])):
                if matrix[i][j]>target:
                    break
                elif matrix[i][j]==target:
                    return True
        return False