661.图片平滑器

题目：

图像平滑器 是大小为 3 x 3 的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。

每个单元格的  平均灰度 定义为：该单元格自身及其周围的 8 个单元格的平均值，结果需向下取整。（即，需要计算蓝色平滑器中 9 个单元格的平均值）。

如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中 4 个单元格的平均值）。

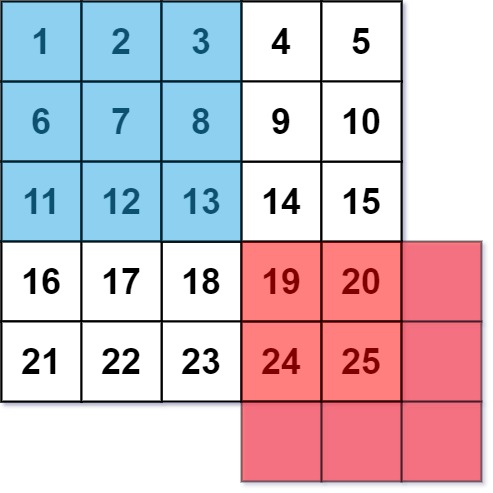
给你一个表示图像灰度的 m x n 整数矩阵 img ，返回对图像的每个单元格平滑处理后的图像 。

示例 1:

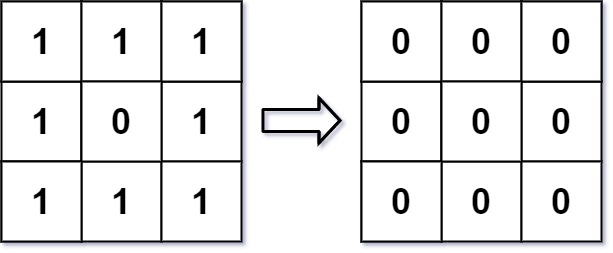
输入:img = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[0, 0, 0],[0, 0, 0], [0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0

示例 2:

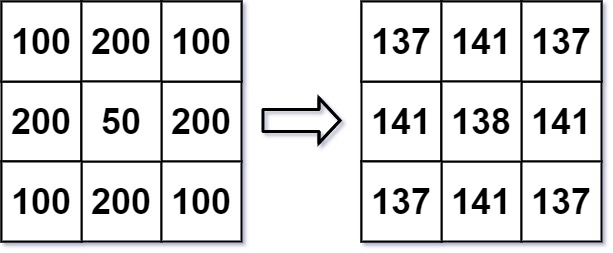
输入: img = [[100,200,100],[200,50,200],[100,200,100]]
输出: [[137,141,137],[141,138,141],[137,141,137]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
对于点 (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
对于点 (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138

提示:

• m == img.length
• n == img[i].length
• 1 <= m, n <= 200
• 0 <= img[i][j] <= 255

解题思路：

 构建一个新的矩阵在原矩阵的基础上加入填充，类似于卷积神经网络加入pedding的想法，然后判断加入的值是否在边缘，用9-边缘个数即可得到需要求均值的个数

代码：

class Solution:
    def imageSmoother(self, img: List[List[int]]) -> List[List[int]]:
        m = len(img)
        n = len(img[0])
        outputs = [[0]*(n+2) for _ in range(m+2)]
        # 先将图像矩阵四周加入0进行填充
        for i in range(m):
            for j in range(n):
                outputs[i+1][j+1] = img[i][j]
        for i in range(m):
            for j in range(n):
                k = 0
                ans = 0
                for flag1 in range(3):
                    for flag2 in range(3):
                        ans += outputs[i+flag1][j+flag2]
                        if i+flag1 == 0 or i+flag1==m+1 or j+flag2==0 or j+flag2==n+1:
                            k+=1
                img[i][j] = int(ans/(9-k))
        return img