6.2.1 图的抽象数据类型
ADT Graph
{
数据对象V:具有相同特性的数据元素的集合,称为顶点集
数据关系R:R = {VR} VR = {<V,W> | <V,W> | V,W ∈ V ^ P(V,W)}
<V,W>表示从V到W的弧,P(V,W)定义了弧<V,W>的信息。
基本操作P:
CreateGraph(*G, V, VR);
初始条件:V是图的顶点集,VR是图中弧的集合。
操作结果:按V和VR的定义构造图G。
DFSTraverse(G)
初始条件:图G已存在。
操作结果:对图进行深度优先遍历。
BFSTraverse(G)
初始条件:图G已存在。
操作结果:对图进行广度优先遍历。
}ADT Graph6.2.2 图的存储结构
图的逻辑结构是多对多。
图没有顺序存储结构,但可以借助二维数组来表示元素间的关系,即数组表示法(邻接距阵)。
图的链式存储结构:

6.2.3 数组(邻接距阵)表示法
建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间的关系)。
设图G = (V,E)有n个顶点,则顶点表vexs:
| i | 0 | 1 | 2 | ... | n |
| vexs | V1 | V2 | V3 | .... | Vn |
图的邻接矩阵(Adjacency Matrix)是一个二维数组G.arcs[n][n],定义为:

无向图的邻接矩阵表示法:

分析1:无向图的邻接距阵是对称的。
分析2:顶点i的度等于第i行(列)中1的个数。
注意:完全图的邻接矩阵中,对角元素为0,其余为1。
有向图的邻接矩阵表示法:
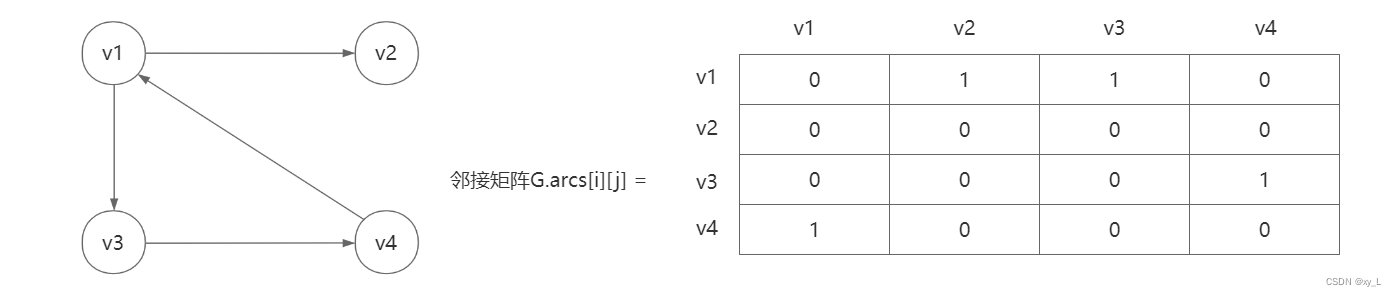
在有向图的邻接矩阵中:
第i行的含义:以顶点vi为尾的弧(即出度边);
第i列的含义:以顶点vi为头的弧(即入度边)。
分析1:有向图的邻接矩阵可能是不对称的。
分析2:顶点的出度等于第i行为1的元素之和,顶点的入度等于第i列为1的元素之和;顶点的度等于第i行为1的元素之和 + 第i列为1的元素之和。
网的邻接距阵表示法:

邻接距阵的存储表:用两个数组分别存储顶点表和邻接矩阵。
邻接矩阵的定义:
#define MVNum 100 //最大顶点数
typedef char VerTexType;
typedef int ArcType;
typedef struct
{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //顶点数和边数
}AMGraph;邻接矩阵的优点:
1、直观、简单、容易理解;
2、方便检查任意一对顶点间是否存在边;
3、方便找任一顶点的所有“邻接点”;
4、方便计算任一顶点的“度”。
邻接距阵的缺点:
1、不便于增加和删除;
2、存放稀疏图是比较浪费空间,适用于稠密图;

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








