RSA算法及Fault Injection攻击数学原理

what

RSA算法是什么以及实现原理，这个不需要我也轮不到我来讲，比较深入浅出的是阮一峰的两篇《RSA算法原理》博客，大家去谷他一歌即可。本文需要读者了解非对称加密的概念。

本文提到RSA算法主要是为了讲Fault Injection（以下简称FI）攻击的数学原理，而讲解FI的数学原理又必须要牵涉到RSA算法的数学原理。实际上，FI攻击不仅可以针对RSA加密算法，也可以针对其他加密算法，不过RSA加密算法的数学原理相对容易理解，相应的FI攻击的数学原理也相对容易理解，所以挑选RSA算法及其对应的FI攻击原理来展开本文。

作为一篇马桶上读物，本文不会牵涉到艰深晦涩的数学公式推导及证明，因为主要一方面是我不会，另一方面本人自从若干年前丧失数学能力之后，一直对那些满篇数学公式猛推如虎的文章深恶痛绝，感到智商受到万吨伤害之余也忍不住想骂一句《大话西游》里的台词：”一天到晚就知道哦哦哦，完全不管人家受得了受不了“。

因此本文不可避免会牵涉一定的数学公式，但我保证都是高中数学范畴，且会用最通俗化的语言解释what、how以及why。

how

假设有两人S（sender）以及R（receiver），S想要通过RSA算法来加密自己的信息发送给R，具体应该怎么做呢？

对于R来说（注意，这里是接收者的公钥及私钥计算过程，而不是想当然的发送者的公钥及私钥计算过程）：

• 第一步，随机选择两个不相等的质数p和q。

假设R选择了61和53，则：

p = 61
q = 53

• 第二步，计算p和q的乘积。

n = p * q = 61 * 53 = 3233

• 第三步，计算n的欧拉函数φ(n)。

欧拉函数的概念：

任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）
计算这个值的方法就叫做欧拉函数，以φ(n)表示。

欧拉函数有如下性质：

1. 如果n是质数，则φ(n) = n - 1
2. 令n = p * q，则φ(n) = φ(p * q) = φ§ * φ(q)
   即，积的欧拉函数等于各个因子的欧拉函数之积。

根据上面的性质，易知：

φ(n) = φ(p * q) = φ(p) * φ(q) = (p - 1) * (q - 1)

R算出来：

φ(n) = 60 * 52 = 3120

• 第四步，随机选择一个整数e，满足1 < e < φ(n)，且e与φ(n)互质。

假设R在1到3120之间，R随机选择了17，则：

e = 17

• 第五步，计算e对于φ(n)的模反元素d。

什么是模反元素呢：

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。记作：

ab ≡ 1 (mod n)

b就叫做a的"模反元素"。

上述概念中的数学公式，等价于计算机编程语言里的表示方法（好理解一些）：

ab % n = 1

套用模反元素的概念可知，我们一定能找到一个整数d，使得ed被φ(n)除的余数为1，即：

ed ≡ 1 (mod φ(n))

该式等价于：

ed - 1 = kφ(n)

于是，找到模反元素d，实质上就是对下面这个二元一次方程求解：

ex + φ(n)y = 1

已知e = 17，φ(n) = 3120，代入上式：

17x + 3120y = 1

此方程可以用”扩展欧几里得算法“求解，此处省略具体求解过程。
总之，R算出一组整数解为(x, y) = (2753, -15)，即：

 d = 2753

• 第六步，将n和e封装成公钥，n和d封装成私钥。

我们的例子里，n = 3233，e = 17，d = 2753，因此公钥为(3233, 17)，私钥为(3233, 2753)。其中，私钥中的d是公钥中的e对于φ(n)的模反元素。

公钥是公开的密钥，也就是说，任何人（当然包括S发送者）都可以知道n和e的值；私钥是只有接收者R自己知道的密钥，也就是说，只有R自己知道d的值。

对于攻击者来说，TA想探取的就是这个私钥，私钥里的n是已知的，剩下需要探取的就是这个d的值。

至于RSA算法的可靠性，阮一峰的博客里有详细证明这里不再赘述。总之结论是，在已知n和e，且n和e的长度满足一定条件的前提下，是无法通过数学推导或在可观的时间内暴力破解出d的，因而保证了私钥的不可破解性。

another how

通过第二节，我们了解了RSA公钥及私钥运算过程，涉及到的数学公式、定理、概念经过去繁存简，也都是一目了然的。

这一节讲解在获取到RSA算法的公钥及私钥后，如何利用公钥私钥体系来进行数据的加密及解密：

• 加密要用公钥(n, e)

假设S要向R发送加密信息m，S先用R的公钥(n, e)对m进行加密（这里注意m必须是整数，字符串可以取ASCII值或unicode值），且m必须小于n。

所谓的“加密”，就是算出下面式子的c：

R的公钥是(3233, 17)，S的m假设是65，代入上式：

于是，计算出的密文c等于2790，S就把2790发送给了R。

注意，这里明文为m，也就是65；经过R的公钥加密后，密文c为2790。

• 解密要用私钥(n, d)

R拿到S发过来的2790（c，密文）后，用自己的私钥(3233, 2753)进行解密。可以证明，下式成立：

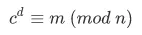
也就是说，c的d次方除以n的余数为m（对n求余为m）。现在c等于2790，私钥是(3233, 2753)，那么R算出：

因此，R知道了S加密前的原文m就是65。

以上就是RSA“加密-解密”的全过程。