机器学习 | 分类评估指标

相关文章：

机器学习 | 目录

机器学习 | 回归评估指标

1. 分类评估指标

评估指标（Evaluation Matrix）：在建立模型后，我们想要知道它的性能如何，因此我们将通过一系列指标来判断一个模型的好坏。

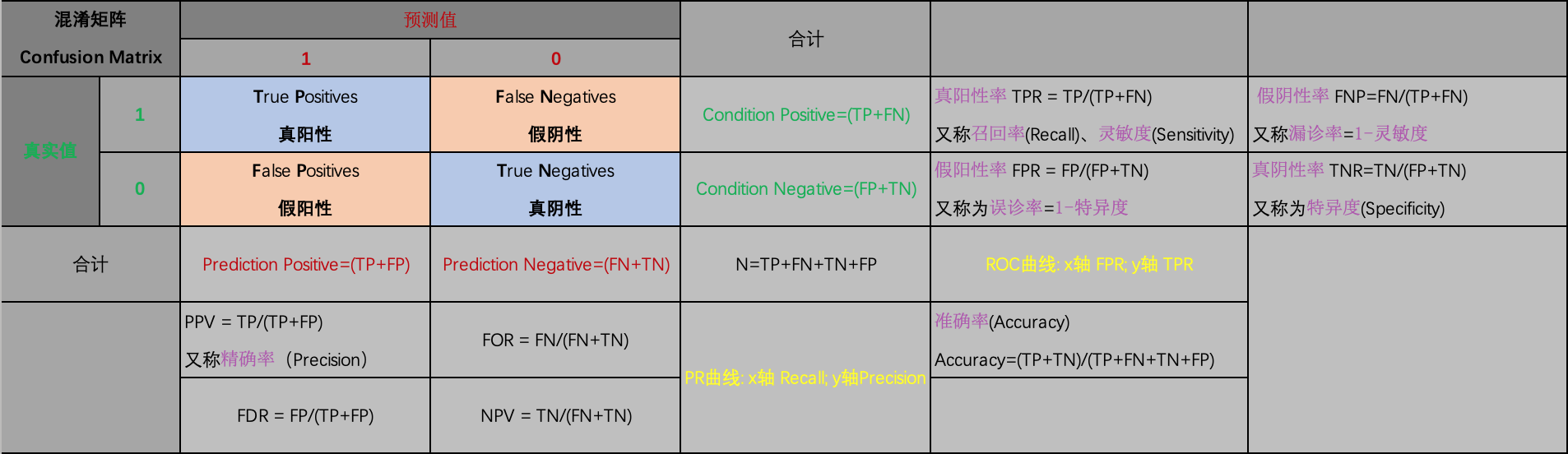
1.1 混淆矩阵 Confusion Matrix

混淆矩阵也称误差矩阵，是表示精度评价的一种标准格式，用$n$行$n$列的矩阵形式来表示。在人工智能中，混淆矩阵（Confusion Matrix）是误差可视化工具，特别用于监督学习；在无监督学习一般叫做匹配矩阵。

混淆矩阵

1. 每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目

2. 每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数目

3. 每一行之和表示该类别的真实样本数量，每一列之和表示被预测为该类别的样本数量

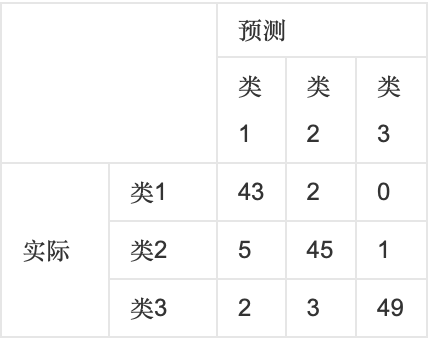
如下图，第一行第一列中的43表示有43个实际归属第一类的实例被预测为第一类，同理，第一行第二列的2表示有2个实际归属为第一类的实例被错误预测为第二类。

1.1.1 scikit-learn 混淆矩阵函数接口

skearn.metrics.confusion_matrix(
    y_true,   # array, Gound true (correct) target values
    y_pred,  # array, Estimated targets as returned by a classifier
    labels=None,  # array, List of labels to index the matrix.
    sample_weight=None  # array-like of shape = [n_samples], Optional sample weights
)

参数设置：

y_true : array, shape = [n_samples]

Ground truth (correct) target values.

y_pred : array, shape = [n_samples]

Estimated targets as returned by a classifier.

labels : array, shape = [n_classes], optional

List of labels to index the matrix. This may be used to reorder or select a subset of labels. If none is given, those that appear at least once in y_true or y_pred are used in sorted order.

sample_weight : array-like of shape = [n_samples], optional

Sample weights.

返回值：

array, shape = [n_classes, n_classes]

Confusion matrix

在 scikit-learn 中, 计算混淆矩阵用来评估分类的准确度。

按照定义, 混淆矩阵$C$中的元素$C_{i,j}$为真实值的为组$i$, 而预测为组$j$的观测数(the number of observations)。

对于二分类任务, 预测结果中：

• 真阳数（True Positives, TP）为$C_{1,1}$
• 真阴数（True Negatives, TN）为$C_{0,0}$
• 假阳数（False Posiives, FN）为$C_{1,0}$
• 假阴数（False Negatives, FN）为$C_{1,0}$

如果 labels 为 None, scikit-learn 会把在出现在 y_true 或 y_pred 中的所有值添加到标记列表 labels 中, 并排好序。^[1]

sklearn.metrics.confusion_matrix 官方文档

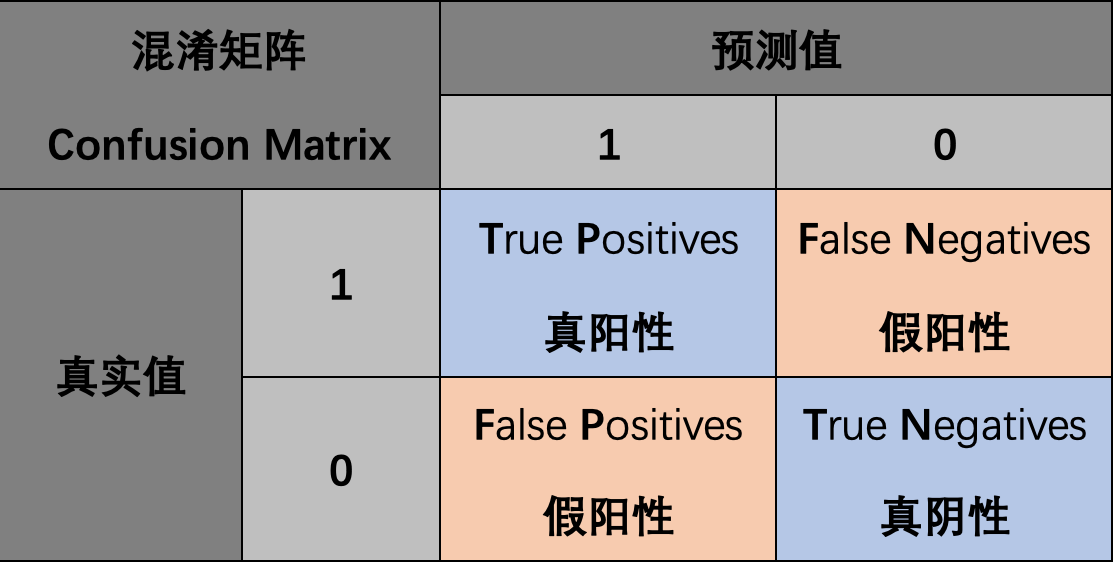
1.2 真阳性TP、假阳性FP、真阴性TN、假阴性FN

对于二分类任务：

• 真阳性（True Positives, TP）为真实值为1，预测值为1，即正确预测出的正样本个数
• 真阴性（True Negatives, TN）为真实值为0，预测值为0，即正确预测出的负样本个数
• 假阳性（False Posiives, FP）为真实值为0，预测值为1，即错误预测出的正样本个数（即数理统计的第一类错误）
• 假阴性（False Negatives, FN）为真实值为1，预测值为0，即错误预测出的负样本个数（即数理统计的第二类错误）

概括地来说：

• 当预测值为1时，体现为阳性；当预测值为0时，体现为阴性
• 当预测值与真实值相符时，为真；当预测值与真实值相反时，为假

阳性、阴性由来：这两个概念是从医学上引进的，一般来说，阳性（+）是表示疾病或体内生理的变化有一定的结果。相反，化验单或报告单上的阴性（－），则多数基本上否定或排除某种病变的可能性。

---

例1. 计算真阳性、假阳性、真阴性、假阴性：

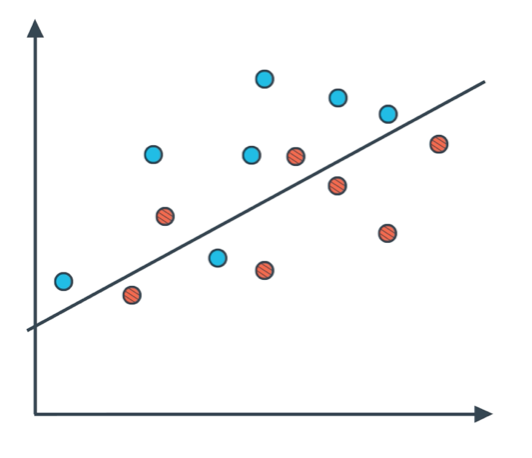
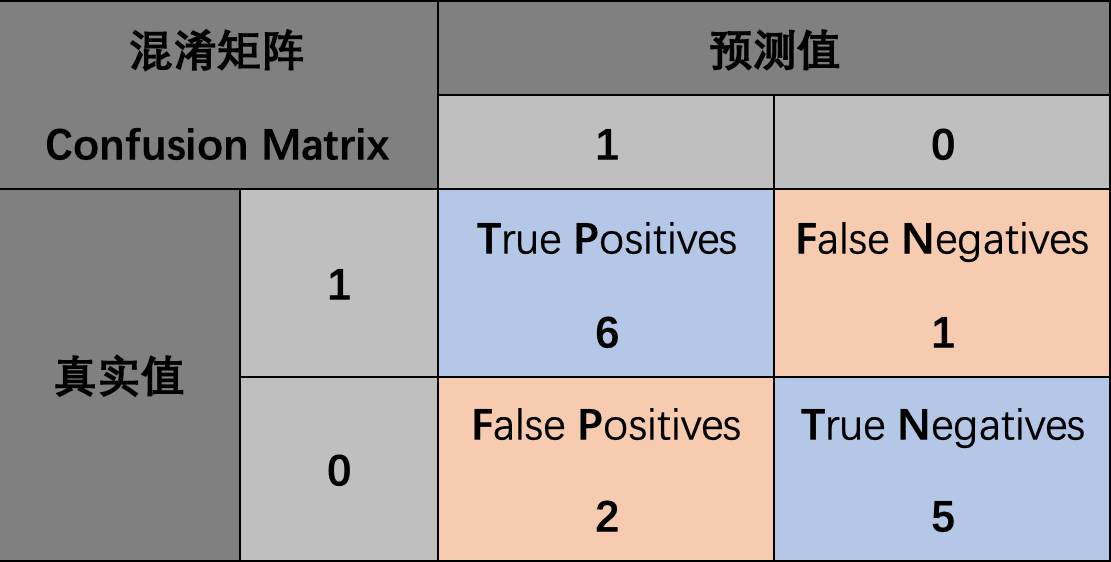
如图所示，蓝色为阳性，红色为阴性；我们训练的模型是一条直线来划分这个区域，阳性区域在上，阴性区域在下。

因此直线上方的点预测值为1，其中6个蓝点的真实值为1，2个两红点的真实值为0，因此真阳性个数为6，假阳性个数为2；直线下方的点预测值为0，其中5个红点真实值为0，1个蓝点真实值为1，因此真阴性个数为5，假阴性个数为1。最终混淆矩阵如下所示：

1.2.1 衍生评估指标

由TP、FP、TN、FN四个指标，可以进一步衍生出其他三个常用的评价分类器性能的指标：

1. 准确率 Accuracy

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}\text{\hspace{1em}(1)}$$

2. 精确率 Precision

$$Precision=\frac{TP}{TP+FP}\text{\hspace{1em}(2)}$$

3. 召回率 Recall

$$Recall=\frac{TP}{TP+FN}\text{\hspace{1em}(3)}$$

我们将会在后面对这些指标进行说明。

这是所有的衍生指标：

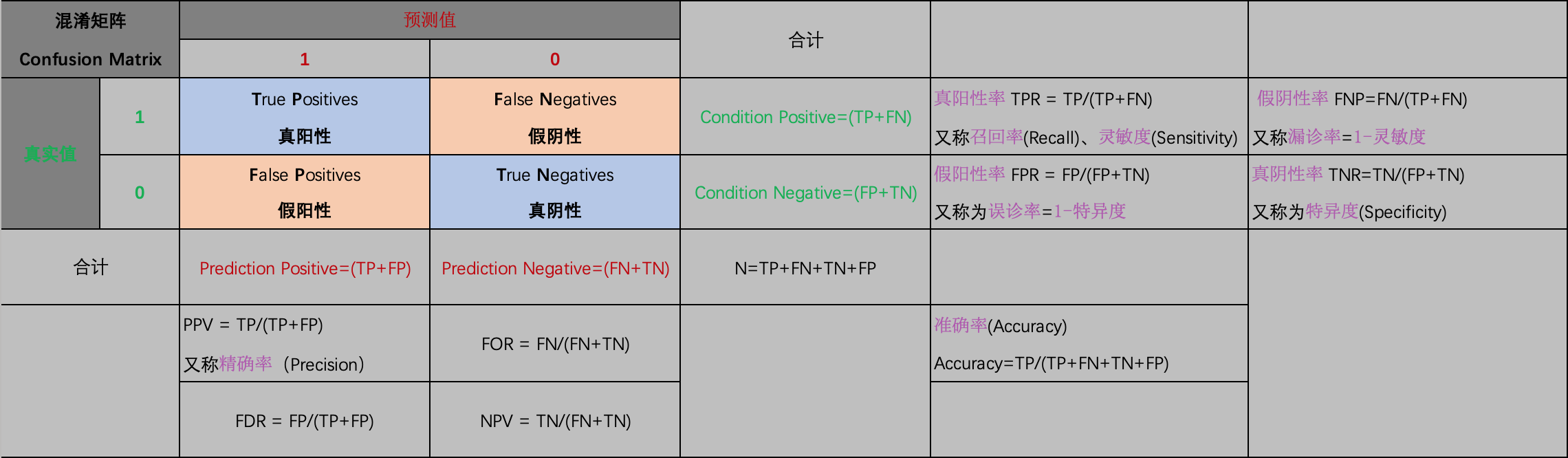
1.3 准确率 Accuracy

准确率（Accuracy）：分类器预测出的正样本中，真实正样本的比例，计算公式如下：

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}\text{\hspace{1em}(4)}$$

---

例2. 假设一个垃圾邮件过滤器模型，在270封垃圾邮件中，正确分类100封，错误分类170封；在730封正常邮件中，正确分类700封，错误分类30封，计算该分类器的准确率：

A c c u r a c y = T P + T N T P + F P + T N + F N = 100 + 700 100 + 30 + 700 + 170 = 80 % Accuracy=\frac{TP+TN}{TP+FP+TN+FN}=\frac{100+700}{100+30+700+170}=80\%