本文深入探讨了GSC（广义旁瓣相消）波束形成器的结构和工作原理，包括其与LCMV的关系，以及如何通过阻塞矩阵B消除期望信号以外的干扰和噪声。通过对线性方程组的解法分析，阐述了在不同情况下GSC的解法，如最小范数解和最小二乘解。GSC利用维纳滤波进一步提升干扰抑制能力，但当声源移动或混响严重时可能造成期望信号失真。
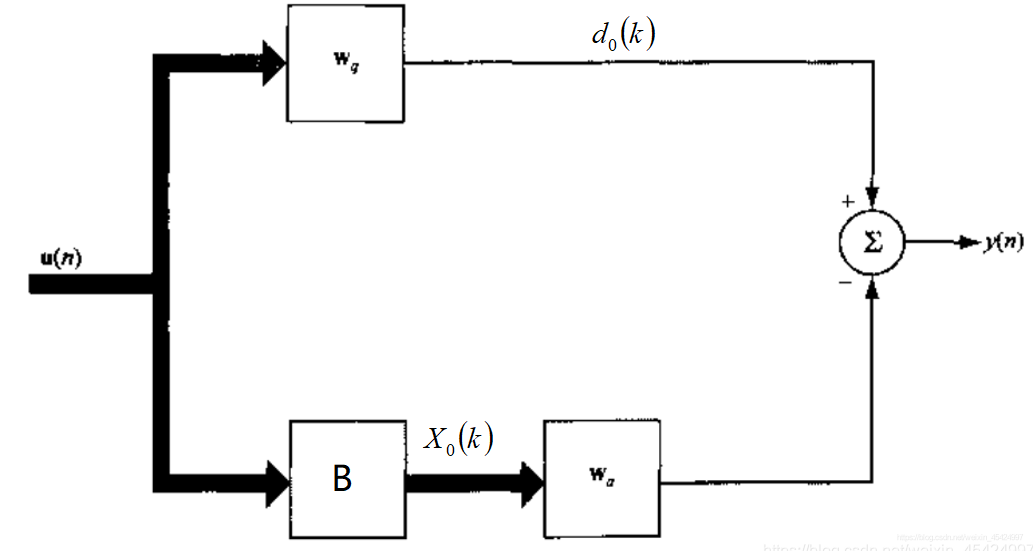
GSC广义旁瓣相消器的结构
如下图所示：
u
(
t
)
=
x
d
(
t
)
⋅
a
(
θ
d
)
+
∑
j
=
1
M
−
1
x
j
(
t
)
⋅
a
(
θ
j
)
+
N
(
t
)
u(t)=x_{d}(t) \cdot a\left(\theta_{d}\right)+\sum_{j=1}^{M-1} x_{j}(t) \cdot a\left(\theta_{j}\right)+N(t)
u(t)=xd(t)⋅a(θd)+j=1∑M−1xj(t)⋅a(θj)+N(t)
某时刻空间中存在M个信号与噪声，其中M-1个为干扰信号,由N个阵列接收,M<N。
并类似于LCMV有如下约束：
C
H
w
q
=
g
(
1
)
\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\mathbf{C}^{H} \mathbf{w}_{q}=\mathbf{g}\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(1)
CHwq=g (1)
C
N
×
M
C_{N \times M}
CN×M是由期望方向和干扰方向导向矢量列向量组成的约束矩阵，
g
=
[
1
0
⋯
0
]
M
×
1
g=\left[\begin{array}{c} 1 \\ 0 \\ \cdots \\ 0 \end{array}\right]_{M \times 1}
g=
10⋯0
M×1
在GSC中
w
q
\mathbf{w}_{q}
wq为固定波束形成权向量
w
q
=
C
(
C
H
C
)
−
1
g
\mathbf{w}_{q}=\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{g}
wq=C(CHC)−1g
这可以理解为对式（1）直接求伪逆即下面的第二种情况
对于线性方程组 A m × n x n × 1 = b m × 1 \mathbf{A}_{m \times n} \mathbf{x}_{n \times 1}=\mathbf{b}_{m \times 1} Am×nxn×1=bm×1
考虑（行/列）满秩的情况，分下面三种情况：
（1）如果m=n,则有唯一解： x = A − 1 b \mathbf{x}=\mathbf{A}^{-1} \mathbf{b} x=A−1b
（2）如果m<n，即方程个数小于未知数个数，此时方程组有无穷多解。为了得到唯一解，必须增加约束条件，要求x的范数最小，这样得到的解称为最小范数解。 x = A H ( A A H ) − 1 b \mathbf{x}=\mathbf{A}^{H}\left(\mathbf{A} \mathbf{A}^{H}\right)^{-1} \mathbf{b} x=AH(AAH)−1b
（3）如果m>n，即方程的个数大于未知数个数，此时方程组不存在精确解，只存在近似解。我们希望找到一个是方程组两边的误差平方和为最小的解，即最小二乘解。 x = ( A H A ) − 1 A H b \mathbf{x}=\left(\mathbf{A}^{H} \mathbf{A}\right)^{-1} \mathbf{A}^{H} \mathbf{b} x=(AHA)−1AHb
可以验证当只存在对期望方向的约束
{
C
=
a
(
θ
d
)
g
=
1
⇒
w
q
=
1
N
a
(
θ
d
)
⇒
d
0
(
k
)
=
w
q
H
u
(
k
)
\left\{\begin{array}{c} C=a\left(\theta_{d}\right) \\ g=1 \end{array} \Rightarrow w_{q}=\frac{1}{N} a\left(\theta_{d}\right) \Rightarrow d_{0}(k)=w_{q}^{H} u(k)\right.
{C=a(θd)g=1⇒wq=N1a(θd)⇒d0(k)=wqHu(k)
w
q
\mathbf{w}_{q}
wq就是Delay-Sum滤波器。阵列接收信号经过DS滤波器后在期望方向有最大的响应，但是他并没有将干扰消除掉，而是降低了干扰信号响应。这时
d
0
(
k
)
d_{0}(k)
d0(k)还是既包含信号，又包含干扰和噪声。为了能进一步降低干扰和噪声，继续进行处理。
GSC首先引入阻塞矩阵B，来阻止期望信号进入辅路。
“向量空间 R n R^{n} Rn包括具有n个元素的列向量。每一个列向量空间都有其子空间，例如向量空间 R 1 R^{1} R1是一条线， R 2 R^{2} R2是一个平面，两者均是 R 3 R^{3} R3的子空间。更一般的讲，如果矩阵 A A A由p个线性无关的N维列向量组成（p<N),即 A = [ a 1 , a 2 , ⋯ , a p ] \mathbf{A}=\left[a_{1}, a_{2}, \cdots, a_{p}\right] A=[a1,a2,⋯,ap],则我们说这些列向量处于矩阵A张成的p维子空间。
如果子空间 V V V中的每一个向量 v v v与子空间 W W W中的每一个向量 w w w正交，即对所有的 v ∈ V , v \in\mathrm{V}, v∈V, 和 w ∈ W , w \in\mathrm{W}, w∈W, 有 v T w = 0 v^{T} w=0 vTw=0,则我们说两个空间 V V V和 W W W正交。 R 3 R^{3} R3中两子空间正交的例子中，两个子空间的维数和等于3（直线维数为1，平面维数为2），因此我们说这两个子空间互为正交补空间。”
− − \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad -- −−《语音增强理论与实践》
对于N个麦克风阵列组成的空间 R N R^{N} RN,将 w q \mathbf{w}_{q} wq所在的的空间称为约束子空间。
约束子空间由约束矩阵 C C C的列向量张成,维度为 N × M N \times M N×M。
约束子空间的正交补空间就是上面提到的B，其维度为 N × ( N − M ) N \times\left(N-M\right) N×(N−M)
分析当只有期望方向约束的情况：
这时只有一个约束，
M
=
1
M=1
M=1约束子空间的维度为
N
×
1
N \times 1
N×1.那么空间中与约束子空间正交的
N
−
1
N-1
N−1个
N
×
1
N \times 1
N×1的基向量构成正交补空间。因为其正交，所以：
B
H
a
(
θ
d
)
=
0
⃗
B^{H} a\left(\theta_{d}\right)=\vec{0}
BHa(θd)=0
所以
u
(
t
)
u(t)
u(t)和阻塞矩阵相乘后，期望信号就为零了，只剩下：
B
H
⋅
u
(
k
)
=
B
H
∑
j
=
1
M
−
1
x
j
(
t
)
⋅
a
⃗
(
θ
j
)
+
B
H
N
⃗
(
t
)
B^{H} \cdot u(k)=B^{H} \sum_{j=1}^{M-1} x_{j}(t) \cdot \vec{a}\left(\theta_{j}\right)+B^{H} \vec{N}(t)
BH⋅u(k)=BHj=1∑M−1xj(t)⋅a(θj)+BHN(t)
如果它能够去逼近DS滤波器滤波后的干扰加噪声部分：
a
⃗
(
θ
d
)
H
⋅
u
(
k
)
=
x
d
(
t
)
+
a
(
θ
d
)
H
∑
j
=
1
M
−
1
x
j
(
t
)
⋅
a
(
θ
j
)
+
a
(
θ
d
)
H
N
(
t
)
\vec{a}\left(\theta_{d}\right)^{H} \cdot u(k)=x_{d}(t)+a\left(\theta_{d}\right)^{H} \sum_{j=1}^{M-1} x_{j}(t) \cdot a\left(\theta_{j}\right)+a\left(\theta_{d}\right)^{H} N(t)
a(θd)H⋅u(k)=xd(t)+a(θd)Hj=1∑M−1xj(t)⋅a(θj)+a(θd)HN(t)
然后再相减，那么输出的就只剩期望信号 x d ( t ) x_{d}(t) xd(t)。
拓展到多个约束的情况：
C
H
B
=
0
B
H
C
=
0
\begin{array}{l} \mathbf{C}^{H} \mathbf{B}=0 \\ \mathbf{B}^{H} \mathbf{C}=\mathbf{0} \end{array}
CHB=0BHC=0
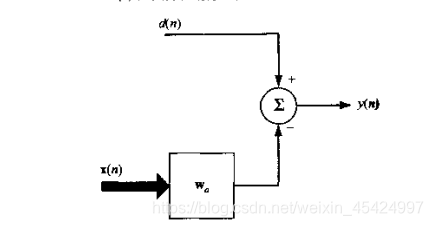
维纳滤波
现在
d
(
n
)
d(n)
d(n)为经过DS滤波后，得到的期望信号+剩余的的干扰和噪声。
x
(
n
)
x(n)
x(n)为
u
(
n
)
u(n)
u(n)经过阻塞矩阵去掉期望信号后，得到的干扰+噪声。
如果通过自适应权
w
a
w_{a}
wa让
x
(
n
)
x(n)
x(n)逼近
d
(
n
)
d(n)
d(n)。由于假设期望信号与干扰和噪声不相关，所以
x
(
n
)
x(n)
x(n)只会去逼近
d
(
n
)
d(n)
d(n)中未完全消除的干扰和噪声量，然后再与
d
(
n
)
d(n)
d(n)做差，就可以得到去掉剩余干扰和噪声后的期望信号。这就是GSC的精髓所在。
将问题转化为维纳滤波的表达形式：
min
w
a
(
d
n
−
w
a
H
x
⃗
(
n
)
)
T
(
d
n
−
w
a
H
x
⃗
(
n
)
)
\min _{{w}_{a}}\left(d_{n}-w_{a}^{H}\vec{x}(n) \right)^{\mathrm{T}}\left(d_{n}-w_{a}^{H}\vec{x}(n)\right)
wamin(dn−waHx(n))T(dn−waHx(n))
其中
x
⃗
(
n
)
=
B
H
⋅
u
(
n
)
\vec{x}(n)=B^{H} \cdot u(n)
x(n)=BH⋅u(n)
d
(
n
)
=
w
q
H
⋅
u
(
n
)
d(n)=w_{q}^{H} \cdot u(n)
d(n)=wqH⋅u(n)
直接带入维纳解的表达式
w
a
=
R
−
1
⋅
P
w_{a}=R^{-1} \cdot P
wa=R−1⋅P
P
=
E
[
B
H
u
(
n
)
u
H
(
n
)
w
q
]
=
B
H
E
[
u
(
n
)
u
H
(
n
)
]
w
q
=
B
H
R
u
w
q
\begin{aligned} {P} &=E\left[{B}^{H} {u}(n) {u}^{H}(n){w}_{q}\right] \\ &={B}^{H} E\left[{u}(n) {u}^{H}(n)\right] {w}_{q} \\ &={B}^{H} R_{u}{w}_{q} \end{aligned}
P=E[BHu(n)uH(n)wq]=BHE[u(n)uH(n)]wq=BHRuwq
R
=
E
[
B
H
u
(
n
)
u
H
(
n
)
B
]
=
B
H
R
u
B
\begin{aligned} {R}_{} &=E\left[{B}^{H} {u}(n) {u}^{H}(n){B}\right] \\ &={B}^{H} R_{u}{B} \end{aligned}
R=E[BHu(n)uH(n)B]=BHRuB
所以GSC的自适应权就可以写为：
w
g
s
c
=
C
(
C
H
C
)
−
1
g
−
B
w
a
=
w
q
−
B
w
a
\mathbf{w}_{g s c}=\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{g}-\mathbf{B} \mathbf{w}_{a}=\mathbf{w}_{q}-\mathbf{B} \mathbf{w}_{a}
wgsc=C(CHC)−1g−Bwa=wq−Bwa
而对于阻塞矩阵B的选取，其可通过 C 的正交补空间中的基构成.
C的正交投影矩阵为介绍：
C
(
C
H
C
)
−
1
C
H
\mathrm{C}\left(\mathrm{C}^{H} \mathrm{C}\right)^{-1} \mathrm{C}^{H}
C(CHC)−1CH
所以 C 的正交补空间的投影矩阵为：
I
−
C
(
C
H
C
)
−
1
C
H
I-C\left(C^{H} C\right)^{-1} C^{H}
I−C(CHC)−1CH
总结
- GSC 是 LCMV 的一种等效实现结构，GSC 结构将 LCMV 的约束优化问题转化为了无约束的优化问题。
- 当 x x x支路中包含较少目标信号时，GSC效果较好；但是当声源移动或者混响比较严重时， x x x中包含的目标信号超过一定程度，将会产生期望信号的泄露，在接下来的自适应滤波过程中会造成噪声信号与上支路期望语音信号相互抵消的现象，导致期望语音的失真，算法性能下降。
推导参考《自适应滤波器原理 第四版》
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
