9-23八股

---

sizeof(数组)和sizeof（指针）

数组名是首元素的地址，当arr作为参数传递时，arr表示首元素的地址；
在sizeof(arr)时，表示整个数组的大小，而不是首元素地址的大小；
&arr：取地址数组名，表示的是整个数组的地址；
，数组在除了3种情况外, 其他时候都要”退化”成指向首元素的指针：

1. 数组名放在sizeof()里，sizeof(s)
2. 对数组取地址，&s;
3. 用来初始化s的”china”;
   除了上述3种情况外,s都会退化成&s[0], 这就是数组变量的操作方式

数组名退化问题

在 C++ 中，数组名退化（也称为“数组名衰减”）指的是当数组作为函数参数传递或用于某些操作时，数组名会自动转换为指向其首元素的指针。这种转换被称为“退化”或“衰减”。
产生退化的几种场景；
1、作为函数参数进行传递，数组名将会退化为指向数组首元素的指针，所以在传递的时候要指明数组的长度；
2、在表达式中使用数组名也会退化为指向首元素的指针；

int arr[5] = {1, 2, 3, 4, 5};
int *p = arr; // 数组名 arr 退化为指向 arr[0] 的指针

3、除了sizeof和&运算符外，大多数情况下都会退化为指针；sizeof会返回整个数组的大小；

数组和指针的差异

1、数组的大小是固定的，而指针只指向一个地址，并不知道指向数组的大小；
2、多维数组退化的时候，会保留指向数组的指针；

int arr[3][4];
int (*p)[4] = arr; // p 是指向包含 4 个整数的数组的指针

函数传值和传引用的区别

传值，函数接收的是参数的副本，不是原始参数；函数内的操作不会影响调用时传递的实参；
传引用：传递的是参数的别名；对引用的操作将会影响传入的实参；
传指针：函数接受的是指向原始对象的内存地址；需要解引用指针操作；

内联函数

一种优化手段：用于避免函数调用时的开销；通过使用inline关键字，编译器会尝试将函数的代码直接插入到函数调用的地方，而不是执行常规的函数调用（压栈、跳转、返回等）

特点

1、跳出函数调用的开销；（栈帧创建、参数传递、跳转、返回等），编译器会将函数体内联展开为代码的一部分；
2、通常用于简单的、频繁调用的小函数；
3、编译器可以忽略inline关键字
4、增大代码体积，代码膨胀；

定义

#include <iostream>

inline int add(int a, int b) {
    return a + b;
}

int main() {
    int x = 5, y = 10;
    std::cout << "Sum: " << add(x, y) << std::endl;
    return 0;
}

使用场景

1、简短、频繁调用的函数；
2、模版类中的成员函数；提高性能；
3、代码和性能权衡；
4、递归函数不能使用，将导致无限展开；

内联函数和宏对比

宏在预处理阶段展开，但无类型检查和作用域限制；相比之下，内联函数具有函数的完整功能，包括类型安全、作用域控制；

总结

内联函数通过将函数调用展开为直接代码，可以减少函数调用的开销，适合用于小而频繁调用的函数。
避免在复杂函数、递归函数、虚函数中使用内联，以避免代码膨胀和编译器优化失败。
内联函数比宏更安全，具有类型检查和作用域限制，是宏的良好替代品

二分法求根号2

1、定义初始区间[]1,2]
2、计算中点：m = （a+b）/2；
3、检查中点：三种情况，等于，小于，大于；
4、m^2 < 2;更新边界；
5、重复步骤，直到区间缩小到足够小，满足精度要求；

#include <iostream>
#include <cmath>

double sqrt2_bisection(double tolerance) {
    double a = 1.0, b = 2.0;
    double mid;
    
    // 二分法开始
    while ((b - a) > tolerance) {
        mid = (a + b) / 2.0;
        
        if (mid * mid < 2.0) {
            a = mid;
        } else {
            b = mid;
        }
    }
    
    // 返回中点作为近似根
    return (a + b) / 2.0;
}

int main() {
    double tolerance = 1e-6; // 设定精度
    double result = sqrt2_bisection(tolerance);
    
    std::cout << "Approximation of sqrt(2): " << result << std::endl;
    std::cout << "Exact value of sqrt(2) (using sqrt function): " << std::sqrt(2) << std::endl;
    return 0;
}

要设定一个误差容限，当循环条件b-a > 误差容限时继续循环，不断更新区间；

牛顿迭代法

开根号的问题可以看作求解f(x) = x2 - a = 0的根。

(1)在曲线f(x)=x^2-a上任取一点(x0,f(x0))，x0≠0，该点的切线方程为：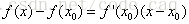
(2)该切线与x轴的交点为：

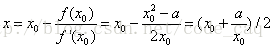
(3)不断用新的交点来更新原来的交点(即逼*的过程)
根据牛顿迭代的原理，可以得到以下的迭代公式：

#include <iostream>
#include <cmath>

double sqrt2_newton(double tolerance) {
    double x = 2.0;  // 初始猜测值，可以选择 1.5 或 2.0
    double next_x;

    while (true) {
        next_x = 0.5 * (x + 2.0 / x);  // 牛顿迭代公式
        
        if (fabs(next_x - x) < tolerance) {  // 判断是否收敛
            break;
        }
        
        x = next_x;  // 更新近似值
    }
    
    return next_x;
}

int main() {
    double tolerance = 1e-6;  // 设置精度
    double result = sqrt2_newton(tolerance);

    std::cout << "Approximation of sqrt(2) using Newton's method: " << result << std::endl;
    std::cout << "Exact value of sqrt(2) (using sqrt function): " << std::sqrt(2) << std::endl;

    return 0;
}

快排

快排是将数组中选组一个基准，然后从数组最左侧和最右侧两个指针，同时往中间跑，左指针寻找大于基准元素的值，右指针寻找小于基准元素的值，找到后交换；交换0次，一次或多次后，左右指针重合，此时一次快排结束，将基准元素和重合元素进行交换；此时本次的基准元素已经找到了最终正确的位置，后面的迭代需要对左部分和右部分进行排序；每一次迭代都有一个元素被排好，就是基准元素；

void QuickSort1(int* a, int begin, int end) {
    if (begin >= end) // 当序列不存在或只有一个元素时，直接返回
        return;

    int left = begin;  // 左指针
    int right = end;   // 右指针
    int keyi = left;   // 基准元素的下标（取序列的第一个元素）

    // 开始分区过程，左右指针向中间移动
    while (left < right) {
        // 右指针向左移动，寻找比基准元素小的元素
        while (left < right && a[right] >= a[keyi]) {
            right--;
        }
        // 左指针向右移动，寻找比基准元素大的元素
        while (left < right && a[left] <= a[keyi]) {
            left++;
        }
        // 如果左指针和右指针尚未相遇，交换这两个不符合顺序的元素
        if (left < right) {
            Swap(&a[left], &a[right]);
        }
    }
    
    // 交换基准元素与相遇点的元素
    int meeti = left;
    Swap(&a[keyi], &a[meeti]);

    // 递归对左右子序列进行排序
    QuickSort1(a, begin, meeti - 1); // 左子序列
    QuickSort1(a, meeti + 1, end);   // 右子序列
}

最优时间复杂度：O(nlogn):每次分区均匀两半；
最坏时间复杂度：O(n^2):每次排序几不平衡，如已排序数组；
平均时间复杂度：O(nlogn);
空间复杂度O(logn)
快排是不稳定的；

平衡树和普通二叉树的区别？为什么使用平衡二叉树

主要区别是结构和性能，特别是在插入、删除、查找操作的时间复杂度；
普通二叉树
插入和删除操作可能导致高度失衡，称为链表，插入、删除、查找的时间复杂度都为O(n);
平衡二叉树
左右子树高度差不超过1；
在插入或删除节点后，会通过旋转等操作维持树的平衡；
最坏情况下，高度为O(logn)；因此查找、删除、插入的时间复杂度为O(logn);

使用二叉树的理解

1、高效的查找性能，在对数级别；
2、快速插入和删除：通过旋转保持高度平衡，保证插入和删除操作的效率；
3、有序性：保证了数据的有序性，方便范围查询和排序操作
4、动态数据集支持；

什么是脏读

一个事务中读取了另一个未提交事务所修改的数据，

数据库的三大范式

九连环接环问题

linux中不占用磁盘空间的目录

/proc目录，是一个虚拟文件系统，存储的是内核和进程的信息，并不实际占用磁盘空间，系统启动时会动态生成这些文件，用于内核交互；

1 2 3 4 5 6 7 8作为叶子结点的权值构造一颗哈夫曼树，其带权路径长度是？

https://blog.youkuaiyun.com/weixin_51350847/article/details/140993301

初始化权值：将每个叶子节点（1, 2, 3, 4, 5, 6, 7, 8）放入一个优先队列（最小堆）。
构建哈夫曼树：
从队列中取出两个最小权值的节点，创建一个新节点，其权值为这两个节点的和。
将新节点放回优先队列。
重复此过程，直到队列中只剩一个节点。
计算带权路径长度：路径长度是节点深度与权值的乘积之和。
带权路径长度=sum(叶子节点的值*路径长度)

使用clock算法进行页面置换，如果物理快都被装满，则最多经过几轮扫描才能到淘汰页面？

https://blog.youkuaiyun.com/D97756228/article/details/131250473
又称最近未用算法（NRU）。该算法将内存中所有页面都通过链接指针链接成一个循环队列，设置访问位，1表示被访问过，0表示未被访问过；如果访问位是0，则选择该页换出，如果访问位是1，则将访问位置0，暂不换出，再按照FIFO算法检查下一个页面，重复上述步骤。
注意：（1）某一页装入主存时，要将访问位置为1，如果该页之后又被访问到，访问位也还是标记成1。
（2）只有发生缺页中断，指针才会移动。
例子：以下面这个页面置换过程为例，访问的页面依次是：1,3,4,2,5,4,7,4。主存有4个空闲的帧

由于有4个空闲帧，最开始访问的4页面依次进入主存，将访问位置为1，没有页面置换，指针不动，此时缺页中断为4；

当页面5进入主存时，主存没有空余的帧且页面5不存在主存中，所以指针向下扫描，依次将访问位修改为0，一轮下来后，指针指向页面1，发现访问位已经为0，将1置换出去，页面5换入主存，修改访问位为1，指针下移到页面3，此时缺页中断为5；
当页面4进入主存时，页面4存在主存中，修改访问位为1，指针不动，不存在缺页中断；
当页面7进入主存时，页面7不在主存中，将3置换出去，页面7换入主存，修改访问位为1，指针下移，此时缺页中断为6；
当页面4进入主存时，页面4存在主存中，指针不动，不存在缺页中断。

结构型模式和行为型模式的功能和特点

https://blog.youkuaiyun.com/zhenliangit0918/article/details/104303707
根据其 目的 （模式是用来做什么的）可分为 创建型 (Creational) ， 结构型 (Structural) 和 行为型 (Behavioral) 三种：
• 创建型模式主要用于 创建对象 。
• 结构型模式主要用于 处理类或对象的组合 。
• 行为型模式主要用于 描述对类或对象怎样交互和怎样分配职责 。
根据 范围 ，即模式主要是用于处理类之间关系还是处理 对象之间的关系，可分为 类模式 和 对象模式 两种：
• 类模式 处理类和子类之间的关系 ，这些关系通过继承建立，在编译时刻就被确定下来，是属于 静态 的。
• 对象模式 处理对象间的关系 ，这些关系在运行时刻变化，更具 动态 性。

创建型

创建型模式 (Creational Pattern) 对类的实例化过程进 行了抽象，能够 将软件模块中对象的创建和对象的使用 分离 。
创建型模式 隐藏了类的实例的创建细节，通 过隐藏对象如何被创建和组合在一起达到使整个系统独 立的目的

结构型

其描述 如何将类或者对 象结合在一起形成更大的结构 ，就像搭积木，可以通过 简单积木的组合形成复杂的、功能更为强大的结构。
结构型模式可以分为 类结构型模式 和 对象结构型模式 ：

行为型模式

行为型模式 (Behavioral Pattern) 是对 在不 同的对象之间划分责任和算法的抽象化 。
行为型模式不仅仅关注类和对象的结构，而 且 重点关注它们之间的相互作用 。 通过行为型模式，可以更加清晰地 划分类与
对象的职责 ，并 研究系统在运行时实例对象 之间的交互 。在系统运行时，对象并不是孤 立的，它们可以通过相互通信与协作完成某 些复杂功能，一个对象在运行时也将影响到 其他对象的运行。

DNS域名系统

分布式系统：DNS采用分布式数据库结构，不同的域名和IP地址信息分散在全球各地的DNS服务器上，降低了单点故障的风险。

层次结构：DNS采用树形结构的命名空间，包括根域、顶级域和子域，便于管理和扩展。

高可用性：通过多个DNS服务器和负载均衡技术，确保域名解析服务的高可用性和冗余性。

缓存机制：DNS解析结果会被缓存，以提高查询效率并减少网络流量。DNS服务器在解析时会使用TTL（生存时间）来控制缓存的有效期。

支持多种记录类型：DNS不仅支持A记录（地址记录），还支持MX（邮件交换记录）、CNAME（别名记录）、NS（名称服务器记录）等多种类型，以满足不同的需求。

动态更新：DNS支持动态更新机制，允许自动更新DNS记录，适用于频繁变动的IP地址环境。

安全性扩展：通过DNSSEC（DNS Security Extensions）等技术，提高域名解析过程的安全性，防止DNS欺骗和缓存投毒等攻击。

人性化：将数字IP地址转换为易于记忆的域名，方便用户访问互联网资源。

DNS系统中的域名中的标签（labels）英文不区分大小写。也就是说，example.com 和 Example.com 被视为相同的域名。这是因为DNS设计时采取了大小写不敏感的原则，以简化用户的输入和记忆。
在DNS域名中，级别最低的域名（即最具体的部分）写在最后。例如，在域名 www.example.com 中，com 是顶级域（TLD），example 是二级域，而 www 是三级域。因此，级别最低的域名部分在最右边。

chmod 753 file

7：读、写、执行
5：读：执行
3：写、执行
顺序以此是：所有者、用户组、其他用户

范式化的优点是什么

消除数据冗余：通过将数据分散到多个表中，减少重复数据的存储，提高存储效率。

提高数据一致性：减少数据的重复项，确保在更新、删除或插入操作时，数据的一致性和完整性更容易维护。

简化数据维护：分离不同的实体和关系，简化对数据库的操作，使得维护和管理变得更加高效。

提高查询效率：在一些情况下，范式化可以优化查询性能，尤其是在需要频繁更新数据的应用中。

提高灵活性：通过结构化的方式组织数据，使得在未来的扩展和修改时更加灵活。

增强数据完整性：通过定义约束（如主键、外键）来确保数据的有效性和完整性，减少数据错误的发生。

通过以上优点，范式化帮助设计出更健壮、更易维护的数据库系统。

vector对象使用等于运算符

对于基本类型，vector是可以直接比较的；
对于自定义类型，确保重载了比较运算符

vector对象下标添加元素

不可以当vector没有分配空间时，进行下标访问会导致未定义；此时应该使用push_back和emplace_back();

auto

类型推断

int x = 10;
int& ref = x; // ref 是一个对 x 的引用
auto a = ref; // a 是 int，值为 10

此种情况下auto并不是引用类型；当使用auto使，如果没有显示的使用&，则推断为值类型；