隐马尔可夫5

1.前向算法

前向概率：给定隐马尔科夫模型$\alpha$，定义到时刻$t$部分观测序列为$o_1,o_2,...,o_t$且状态为$q_i$的概率为前向概率，记作
$${\alpha }_t(i)=P(o_1,o_2,...,o_t,i_t=q_i|\lambda )$$

直接看例子：
考虑盒子和球模型$\lambda =(A,B,\pi )$,状态集合Q={1,2,3},观测集合V={红，白}。

设$T=3,O=(红，白，红)$，试用前向算法计算$P(O|\lambda )$。
（1）计算处初值

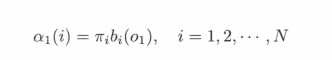
因为第一个时刻是红色，所以
隐藏状态盒子1的概率
$\alpha 1(1)=\pi 1b1(o1)=0.2\times 0.5=0.1$
隐藏状态盒子2的概率
$\alpha 1(2)=\pi 2b2(o1)=0.4\times 0.4=0.16$
隐藏状态盒子3的概率
$\alpha 1(3)=\pi 3b3(o1)=0.4\times 0.7=0.28$

现在我们可以开始递推了，首先递推时刻2三个状态的前向概率：
时刻2是白色球，隐藏状态是盒子1的概率为：
$\alpha 2(1)=[\sum i=13\alpha 1(i)ai1]b1(o2)=[0.1\ast 0.5+0.16\ast 0.3+0.28\ast 0.2]\times 0.5=0.077$
隐藏状态是盒子2的概率为：
$\alpha 2(2)=[\sum i=13\alpha 1(i)ai2]b2(o2)=[0.1\ast 0.2+0.16\ast 0.5+0.28\ast 0.3]\times 0.6=0.1104$
隐藏状态是盒子3的概率为：
$\alpha 2(3)=[\sum i=13\alpha 1(i)ai3]b3(o2)=[0.1\ast 0.3+0.16\ast 0.2+0.28\ast 0.5]\times 0.3=0.0606$

继续递推，现在我们递推时刻3三个状态的前向概率：

时刻3是红色球，隐藏状态是盒子1的概率为：
$\alpha 3(1)=[\sum i=13\alpha 2(i)ai1]b1(o3)=[0.077\ast 0.5+0.1104\ast 0.3+0.0606\ast 0.2]\times 0.5=0.04187$
隐藏状态是盒子2的概率为：
$\alpha 3(2)=[\sum i=13\alpha 2(i)ai2]b2(o3)=[0.077\ast 0.2+0.1104\ast 0.5+0.0606\ast 0.3]\times 0.4=0.03551$
隐藏状态是盒子3的概率为：
$\alpha 3(3)=[\sum i=13\alpha 2(i)ai3]b3(o3)=[0.077\ast 0.3+0.1104\ast 0.2+0.0606\ast 0.5]\times 0.7=0.05284$

最终我们求出观测序列:O={红，白，红}的概率为：

$P(O|\lambda )=\sum i=13\alpha 3(i)=0.13022$