C++中的博弈问题

C++中的博弈问题

本文仅讨论符合以下条件的博弈问题
1、当前状态不是先手必胜态就是先手必败态。
2、若当前状态存在一种转化为先手必败态的方式，则当前状态为先手必胜态。
3、若当前状态不存在一种转化为先手必败态的方式，则当前状态为先手必败态。

那么一般的博弈问题，失败条件是已知的，而失败状态就为一种先手必败态。当你知道先手必败态，就可以跟上述3大规则来把跟博弈中的所有状态表示出来。
圆圈表示状态
线条表示转换
1代表胜利
X代表失败
空缺代表未知
则已知一个博弈问题的所有状态如下。

则根据上述3大规则
我们可以推导出所有状态

所以该博弈先手必胜
引出SG函数，

首先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

（摘自百度百科）

我们定义每个状态可以延伸到的所有状态的sg函数值，为该点的子集。
该点的sg值为该点的mex值
我们的图就变成

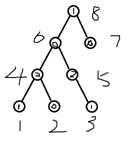
举个例子对于点4，他可以衍生到点1和点2，sg分别为1、0，所以当前点的sg值为2。
我们可以发现，sg值为0的点是先手必败，大于0的点