JavaScript 中 0.1 + 0.2 的精度以及数字类型的整理

最新推荐文章于 2025-06-28 10:35:38 发布

原创最新推荐文章于 2025-06-28 10:35:38 发布 · 697 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#程序员

web前端同时被 2 个专栏收录

35 篇文章

订阅专栏

程序员

32 篇文章

订阅专栏

JavaScript 中数字是如何表示的

JavaScript 中的所有数字都是浮点数，使用 64 位二进制来表示，也叫做双精度浮点型，这种方式出自于 IEEE-754 标准。

64 位二进制的表达方式

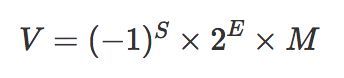
计算公式

公式解读

S (Sign/1bit)：符号部分，当 S=0，V 为正数；当 S=1，V 为负数。
E (Exponent/8bits)：指数部分。E 是一个无符号整数，因为长度是11位，取值范围是 0~2047。但是科学计数法中的指数是可以为负数的，所以人们约定减去一个中间数 1023， [0,1022] 表示为负， [1024,2047] 表示为正
M (Mantissa/23bits)：表示有效数字，大于等于1，小于2。第一位 1 可以被舍去，只保留小数部分节省一位有效数字。

指数 E 还分为三种情况：

E 不全为 0 或不全为 1。这时，浮点数就采用上面的规则表示，即指数 E 的计算值减去 127（或 1023 ），得到真实值，再将有效数字 M 前加上第一位的 1。
E 全为 0。这时，浮点数的指数 E 等于 1-127（或者 1-1023 ），有效数字 M 不再加上第一位的 1，而是还原为 0.xxxxxx 的小数。这样做是为了表示 ± 0，以及接近于 0 的很小的数字。
E 全为 1。这时，如果有效数字 M 全为 0，表示 ± 无穷大（正负取决于符号位s）；如果有效数字 M 不全为 0，表示这个数不是一个数（NaN）。

2^E 代表什么：

上面的公式其实是科学计数法的表示方式，十进制中我们如果想要对小数点进行前移或后移，就是 (一个数 :heavy_multiplication_x: 10^1) 表示小数点往后移一位，同样的在二进制中就是采用（一个二进制数 :heavy_multiplication_x: 2^1）表示二进制表达的数字的小数点往后移一位。

IEEE 754 中规定：

对于 32 位的浮点数，最高的 1 位是符号位 S，接着的 8 位是指数 E，剩下的 23 位为有效数字 M；

对于 64 位的浮点数，最高的 1 位是符号位 S，接着的11位是指数 E，剩下的 52 位为有效数字 M。

0.1 + 0.3 !== 0.3

> 0.1 + 0.2
0.30000000000000004

0.1 和 0.2 转换成 2 进制

> (0.1).toString(2)
"0.0001100110011001100110011001100110011001100110011001101"

> (0.2).toString(2)
"0.001100110011001100110011001100110011001100110011001101"

// 0.1 + 0.2
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111

// 转成十进制正好是 0.30000000000000004

误差怎么来的？

由于 IEEE 754 的规定，用 64 位二进制来表示数字，如果我们手动去转换一下十进制的 0.1到二进制， 1100部分是会一直循环下去，显然如果你找一个位置阶段只取其中的一部分值的话，精度就不准确了，而【M (Mantissa/23bits)：表示有效数字】只有 52 位可以存储,看一下转换的过程

// 0.1 -> 二进制表示
0001100110011001100110011001100110011001100110011001100(1100一直循环下去)

// 按照 IEEE 754 的规定，套公式，用科学计数法表示成 1.xxx * 2^-x 的方式，所以小数点往后移
1.100110011001100110011001100110011001100110011001100(1100一直循环下去)

// 小数点后的这部分是尾数，尾数长度 == 小数值精度 == 尾数所代表二进制的个数越多就越精确，而按照规定我们只有 52 位，超出的能进位就进位，所以最终表示为
1.100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 11010

这么一来，像 0.1 这样的数值就不是精确的，不精确的两个数值做运算，结果显而易见，这里有个网站可以将二进制的展示方式表现出来。

0.1 digits visualization

另外根据二进制转换为十进制的公式，如果你使用 Math.pow() 去计算的话，会发现结果就是 0.1 ，然而我经过手算( 0.1.toString(2) 转换为十进制)后实际结果是和 0.1.toPrecision(x)相近的，因为我是按照实际保留的尾数进行计算的，精度上没有 0.1.toPrecision(x) 高，但是在相同精度内结果是一致。

> Math.pow(2,-4) + 
Math.pow(2,-5) + 
Math.pow(2,-8) + 
Math.pow(2,-9) + 
Math.pow(2,-12) + 
Math.pow(2,-13) +
Math.pow(2,-16) + 
Math.pow(2,-17) + 
Math.pow(2,-20) + 
Math.pow(2,-21) + 
Math.pow(2,-24) + 
Math.pow(2,-25) +
Math.pow(2,-28) + 
Math.pow(2,-29) + 
Math.pow(2,-32) + 
Math.pow(2,-33) + 
Math.pow(2,-36) + 
Math.pow(2,-37) +
Math.pow(2,-40) +
Math.pow(2,-41) +
Math.pow(2,-44) +
Math.pow(2,-45) +
Math.pow(2,-48) +
Math.pow(2,-49) +
Math.pow(2,-52) +
Math.pow(2,-53) +
Math.pow(2,-55)
0.1

0.1.toPrecision(29)
"0.10000000000000000555111512313"

可以＋web前端扣扣裙：939106847 免费网课在线学习以及问题解答、项目指导服务，配合强大的学习工具，带你完成九大实战项目，经历从零基础到专业前端工程师的完美蜕变。

欢迎初学和进阶中的小伙伴。裙里有免费的学习资料，还有专业老师为你解惑，更有免费体验课、免费直播课等福利不定期放送。