训练营第二十九天贪心(简单题目)

455.分发饼干
题目
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
解答
方法一:
优先考虑饼干,小饼干先喂饱小胃口
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0;
int i = 0;
int j = 0;
while (i < g.length && j < s.length){
if (g[i] <= s[j]){
count++;
i++;
}
j++;
}
return count;
}
}
方法二:
先考虑小孩,先喂饱胃口大的
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int count = 0;
int i = g.length - 1;
int j = s.length - 1;
while (i >= 0 && j >= 0){
if (g[i] <= s[j]){
count++;
j--;
}
i--;
}
return count;
}
}
376.摆动序列
题目
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 **摆动序列 。**第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
- 例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5]
输出:6
解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8]
输出:7
解释:这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9]
输出:2
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
解答
局部最优
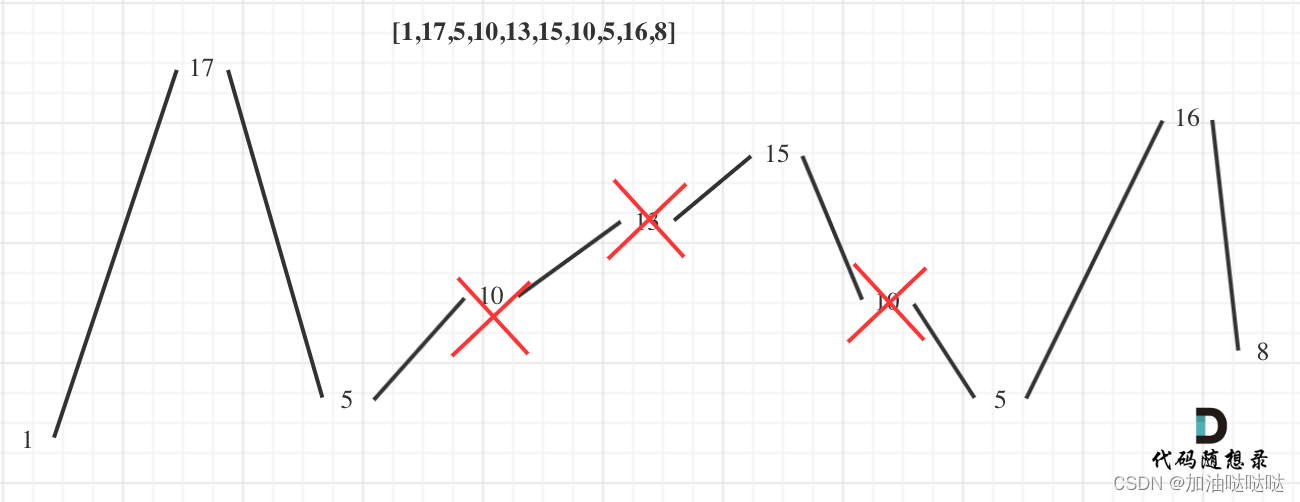
每次都找最大的,也就是每次如果不满足条件,left与right都为符号一致,是单调的时,舍弃差值小的,每次只找坡度最大的,这样可以使下一次的差值的符号一定与当前符号相反
情况一:上下坡中有平坡


情况二:数组首尾两端

解决
int left = 0;
从左向右删,如果left是0,并且right不为0,那么将第一个2删除
情况三:单调坡度有平坡

应该把三个2都删掉,所以为了避免left的不必要更新,将对left的更新放在if中,如果放在if外就是错的
class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums.length <= 1) return nums.length;
int left = 0;//记录第一轮的pre
int count = 1;
for (int i = 1; i < nums.length; i++) {
int right = nums[i] - nums[i - 1];//第一轮为第二个-第一个
//此时的left就是0,会在下面的if中有判断
if (right > 0 && left <= 0 || right < 0 && left >= 0){
count++;
left = right;//更新left为上一轮的pre
//在if里更新是因为避免出现单调坡度有平坡
}
}
return count;
}
}
53.最大子序和
题目
-
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
输入:nums = [1] 输出:1示例 3:
输入:nums = [5,4,-1,7,8] 输出:23提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
解答
局部最优,如果是【1,-2,1】,那么要保证局部最优
- 第一次当前和为1,更新sum并与max比较
- 第二次-2,和变成了-1,那么此时的和为负数,只要加上下一轮就会导致下一个元素+当前的和更小,那么就不是局部最优,要舍弃,此时使用max记录最大值并重置sum
- 第三次起始位置变为1,sum被更新,只有当sum比max大时,才会更新max
局部最优也就是保证和在当前情况下是最优,如果为负数,那么也就不一定是最优,因为再加上下一个元素一定会减小
class Solution {
public int maxSubArray(int[] nums) {
int sum = 0;//记录当前字串的和
int max = Integer.MIN_VALUE;//记录最终的返回值
for (int num : nums) {
sum += num;
max = Math.max(sum,max);
if (sum < 0)//如果<0,那么下一次一定就不是局部最优,下一次从头开始
sum = 0;
}
return max;
}
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








