第二章 数组与链表

第二章 数组与链表

参考文章：https://www.hello-algo.com/

2.1、数组

---

数组是一种线性数据结构，用于存储相同类型的元素。数组中的元素存储在连续的内存空间中，每个元素的位置称为索引。数组的主要特点是通过索引可以快速访问任意元素，时间复杂度为 O(1)。

2.1.1、数组的常用操作

1. 初始化数组

• 可以通过指定长度初始化数组，例如 [0] * 5 创建一个长度为 5 的数组，所有元素初始化为 0。

• 也可以通过指定初始值初始化数组，例如 [1, 3, 2, 5, 4]。

• 示例代码

  /* 随机访问元素 */
  int randomAccess(int[] nums) {
      // 在区间 [0, nums.length) 中随机抽取一个数字
      int randomIndex = ThreadLocalRandom.current().nextInt(0, nums.length);
      // 获取并返回随机元素
      int randomNum = nums[randomIndex];
      return randomNum;
  }
  

2.访问元素

• 数组元素的内存地址可以通过公式计算：地址 = 基地址 + 索引 × 元素大小。

• 访问元素的时间复杂度为 O(1)。

• 示例代码

  /* 随机访问元素 */
  int randomAccess(int[] nums) {
      // 在区间 [0, nums.length) 中随机抽取一个数字
      int randomIndex = ThreadLocalRandom.current().nextInt(0, nums.length);
      // 获取并返回随机元素
      int randomNum = nums[randomIndex];
      return randomNum;
  }
  

3.插入元素

• 在数组中间插入元素需要将插入点之后的所有元素向后移动一位，时间复杂度为 O(n)。

• 示例代码（Java）：

  /* 在数组的索引 index 处插入元素 num */
  void insert(int[] nums, int num, int index) {
      // 把索引 index 以及之后的所有元素向后移动一位
      for (int i = nums.length - 1; i > index; i--) {
          nums[i] = nums[i - 1];
      }
      // 将 num 赋给 index 处的元素
      nums[index] = num;
  }
  

4.删除元素

• 删除元素需要将删除点之后的所有元素向前移动一位，时间复杂度为 O(n)。

• 示例代码（Java）：

  /* 删除索引 index 处的元素 */
  void remove(int[] nums, int index) {
      // 把索引 index 之后的所有元素向前移动一位
      for (int i = index; i < nums.length - 1; i++) {
          nums[i] = nums[i + 1];
      }
  }
  

5.遍历数组

• 可以通过索引遍历数组，也可以直接遍历数组中的每个元素。

• 示例代码（Java）：

  /* 遍历数组 */
  void traverse(int[] nums) {
      int count = 0;
      // 通过索引遍历数组
      for (int i = 0; i < nums.length; i++) {
          count += nums[i];
      }
      // 直接遍历数组元素
      for (int num : nums) {
          count += num;
      }
  }
  

6.查找元素

• 线性查找：遍历数组，找到目标值返回其索引，否则返回 -1。时间复杂度为 O(n)。

• 示例代码（Java）：

  /* 在数组中查找指定元素 */
  int find(int[] nums, int target) {
      for (int i = 0; i < nums.length; i++) {
          if (nums[i] == target)
              return i;
      }
      return -1;
  }
  

7.扩容数组

• 数组长度固定，扩容需要创建一个更大的数组，并将原数组元素复制到新数组中。时间复杂度为 O(n)。

• 示例代码（Java）：

  /* 扩展数组长度 */
  int[] extend(int[] nums, int enlarge) {
      // 初始化一个扩展长度后的数组
      int[] res = new int[nums.length + enlarge];
      // 将原数组中的所有元素复制到新数组
      for (int i = 0; i < nums.length; i++) {
          res[i] = nums[i];
      }
      // 返回扩展后的新数组
      return res;
  }
  

2.2、数组的优点与局限性

• 优点：
  • 空间效率高：数组分配连续内存块，无额外结构开销。
  • 支持随机访问：可以在 O(1) 时间内访问任意元素。
  • 缓存局部性：访问一个元素时，其周围的元素也会被缓存，提升操作效率。
• 局限性：
  • 插入与删除效率低：需要移动大量元素，时间复杂度为 O(n)。
  • 长度不可变：扩容需要复制数据到新数组，开销较大。
  • 空间浪费：如果分配的大小超过实际需求，会造成内存浪费。

2.3、数组的典型应用

• 随机访问：用于随机抽样，例如生成随机索引访问数组元素。
• 排序和搜索：数组是排序（如快速排序、归并排序）和搜索（如二分查找）算法的基础。
• 查找表：可以将数据映射到数组中，例如通过 ASCII 码值作为索引存储字符。
• 机器学习：数组是神经网络中向量、矩阵、张量运算的基础。
• 数据结构实现：数组可用于实现栈、队列、哈希表、堆、图等复杂数据结构。

2.2、链表

---

链表是一种线性数据结构，由一系列节点组成，每个节点包含两部分：

1. 值（Value）：存储数据。
2. 引用（Pointer/Reference）：指向下一个节点的地址。

链表的特点：

• 灵活性：节点可以分散存储在内存的任意位置，无需连续空间。
• 动态性：链表的长度可以动态变化，适合处理不确定数量的数据。
• 内存占用：每个节点除了存储数据外，还需要额外存储指向下一个节点的引用，因此内存占用比数组稍多。
  

链表的常用操作

1. 初始化链表

   • 创建节点对象，并通过引用将节点连接起来。

   • 示例代码：

     /* 链表节点类 */
     class ListNode {
         int val;        // 节点值
         ListNode next;  // 指向下一节点的引用
         ListNode(int x) { val = x; }  // 构造函数
     }
     

   • 初始化链表 1 -> 3 -> 2 -> 5 -> 4：

     n0 = ListNode(1)
     n1 = ListNode(3)
     n2 = ListNode(2)
     n3 = ListNode(5)
     n4 = ListNode(4)
     n0.next = n1
     n1.next = n2
     n2.next = n3
     n3.next = n4
     
     

2. 插入节点

   

   • 在链表中插入节点只需改变两个节点的引用，时间复杂度为 O(1)。

   • 示例代码：

     /* 在链表的节点 n0 之后插入节点 P */
     void insert(ListNode n0, ListNode P) {
         ListNode n1 = n0.next;
         P.next = n1;
         n0.next = P;
     }
     

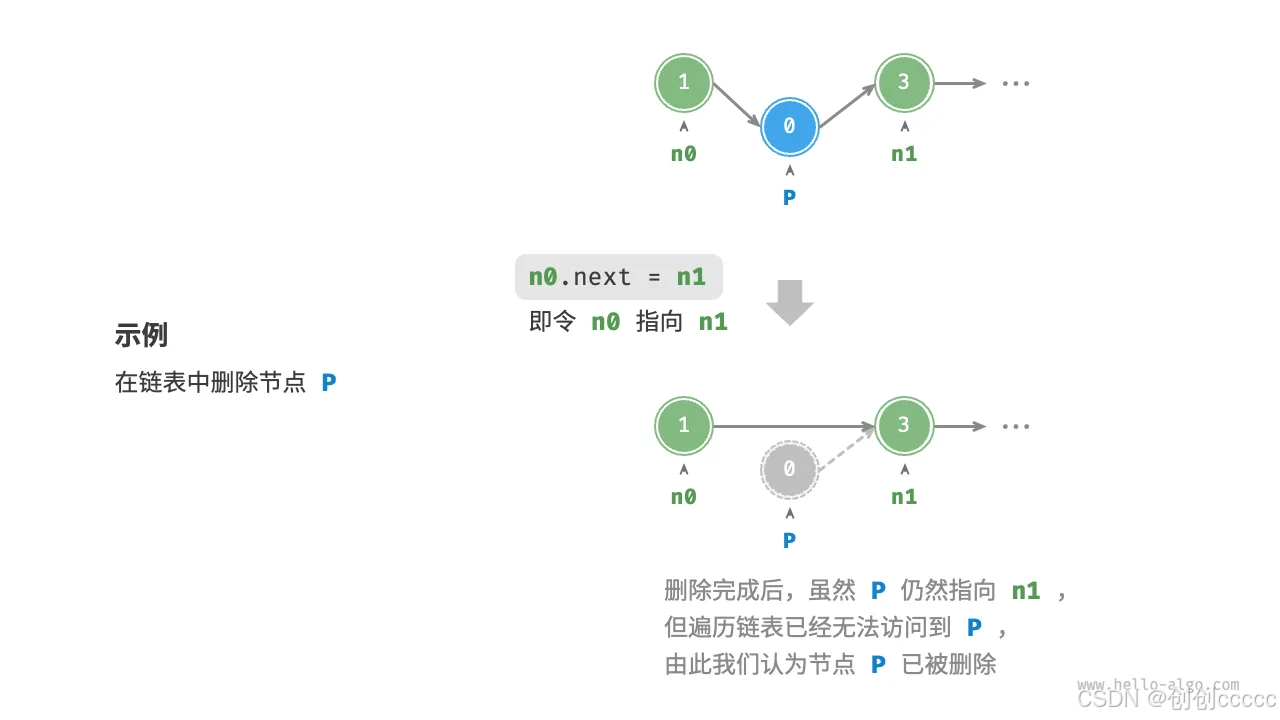
3. 删除节点

   

   • 删除链表中的节点只需改变一个节点的引用，时间复杂度为 O(1)。

   • 示例代码：

     /* 删除链表的节点 n0 之后的首个节点 */
     void remove(ListNode n0) {
         if (n0.next == null)
             return;
         // n0 -> P -> n1
         ListNode P = n0.next;
         ListNode n1 = P.next;
         n0.next = n1;
     }
     

4. 访问节点

   • 从头节点开始逐个遍历，直到找到目标节点，时间复杂度为 O(n)。

   • 示例代码：

     /* 访问链表中索引为 index 的节点 */
     ListNode access(ListNode head, int index) {
         for (int i = 0; i < index; i++) {
             if (head == null)
                 return null;
             head = head.next;
         }
         return head;
     }
     

5. 查找节点

   • 遍历链表，查找值为 target 的节点，返回其索引，时间复杂度为 O(n)。

   • 示例代码：

     /* 在链表中查找值为 target 的首个节点 */
     int find(ListNode head, int target) {
         int index = 0;
         while (head != null) {
             if (head.val == target)
                 return index;
             head = head.next;
             index++;
         }
         return -1;
     }
     

数组 vs. 链表

特性	数组	链表
存储方式	连续内存空间	分散内存空间
容量扩展	长度不可变	可灵活扩展
内存效率	元素占用内存少，但可能浪费空间	元素占用内存多
访问元素	O(1)	O(n)
添加/删除元素	O(n)	O(1)

常见链表类型

1. 单向链表
   • 最基本的链表形式，每个节点指向下一个节点。
   • 适合简单的线性操作。
2. 环形链表
   • 将单向链表的尾节点指向头节点，形成环形。
   • 适合循环操作，如时间片轮转调度算法。
3. 双向链表
   • 每个节点包含两个引用，分别指向前驱节点和后继节点。
   • 适合需要双向遍历的场景，如浏览器历史记录、LRU缓存。

链表的典型应用

1. 栈与队列
   • 单向链表可用于实现栈（后进先出）和队列（先进先出）。
2. 哈希表
   • 链式地址法解决哈希冲突，冲突的元素存储在链表中。
3. 图
   • 邻接表表示图，每个顶点对应一个链表，存储与该顶点相连的其他顶点。
4. 高级数据结构
   • 红黑树、B树等需要访问父节点的结构，类似双向链表。
5. 浏览器历史
   • 使用双向链表快速访问前一个和后一个网页。
6. LRU缓存
   • 使用双向链表快速插入、删除节点，并访问最近最少使用的数据。

2.3、列表

---

定义

• 列表（List） 是一种抽象的数据结构，表示元素的有序集合。
• 支持元素的访问、修改、添加、删除和遍历等操作。
• 列表可以基于链表或数组实现。

特性

• 基于链表的列表：支持动态扩容，适合频繁的增删操作。
• 基于数组的列表：支持快速访问和更新，但长度固定，扩容机制复杂。
• 动态数组：结合了数组的高效访问和链表的动态扩容特性，是现代编程语言中列表的常见实现方式（如 Python 的 list、Java 的 ArrayList、C++ 的 vector 等）。

列表的常用操作

1. 初始化列表
   • 无初始值：nums = []
   • 有初始值：nums = [1, 3, 2, 5, 4]
2. 访问元素
   • 时间复杂度：O(1)
   • 示例：num = nums[1]（访问索引为 1 的元素）
3. 插入与删除元素
   • 在尾部添加元素：时间复杂度 O(1)
   • 在中间或头部插入/删除元素：时间复杂度 O(n)
   • 示例：
     • 添加：nums.append(6)
     • 插入：nums.insert(3, 6)
     • 删除：nums.pop(3)
4. 遍历列表
   • 通过索引遍历：for i in range(len(nums))
   • 直接遍历：for num in nums
5. 拼接列表
   • 将一个列表拼接到另一个列表的尾部：nums += nums1
6. 排序列表
   • 排序后可以使用二分查找和双指针算法。
   • 示例：nums.sort()

列表的实现

许多编程语言内置了列表，例如 Java、C++、Python 等。它们的实现比较复杂，各个参数的设定也非常考究，例如初始容量、扩容倍数等。感兴趣的读者可以查阅源码进行学习。

为了加深对列表工作原理的理解，我们尝试实现一个简易版列表，包括以下三个重点设计：

• 初始容量：选择合适的初始容量（如 10）。
• 数量记录：使用变量 size 记录当前元素数量。
• 扩容机制：当容量不足时，扩容为原容量的倍数（如 2 倍）。

代码示例（Java）：

/* 列表类 */
class MyList {
    private int[] arr; // 数组（存储列表元素）
    private int capacity = 10; // 列表容量
    private int size = 0; // 列表长度（当前元素数量）
    private int extendRatio = 2; // 每次列表扩容的倍数

    /* 构造方法 */
    public MyList() {
        arr = new int[capacity];
    }

    /* 获取列表长度（当前元素数量） */
    public int size() {
        return size;
    }

    /* 获取列表容量 */
    public int capacity() {
        return capacity;
    }

    /* 访问元素 */
    public int get(int index) {
        // 索引如果越界，则抛出异常，下同
        if (index < 0 || index >= size)
            throw new IndexOutOfBoundsException("索引越界");
        return arr[index];
    }

    /* 更新元素 */
    public void set(int index, int num) {
        if (index < 0 || index >= size)
            throw new IndexOutOfBoundsException("索引越界");
        arr[index] = num;
    }

    /* 在尾部添加元素 */
    public void add(int num) {
        // 元素数量超出容量时，触发扩容机制
        if (size == capacity())
            extendCapacity();
        arr[size] = num;
        // 更新元素数量
        size++;
    }

    /* 在中间插入元素 */
    public void insert(int index, int num) {
        if (index < 0 || index >= size)
            throw new IndexOutOfBoundsException("索引越界");
        // 元素数量超出容量时，触发扩容机制
        if (size == capacity())
            extendCapacity();
        // 将索引 index 以及之后的元素都向后移动一位
        for (int j = size - 1; j >= index; j--) {
            arr[j + 1] = arr[j];
        }
        arr[index] = num;
        // 更新元素数量
        size++;
    }

    /* 删除元素 */
    public int remove(int index) {
        if (index < 0 || index >= size)
            throw new IndexOutOfBoundsException("索引越界");
        int num = arr[index];
        // 将将索引 index 之后的元素都向前移动一位
        for (int j = index; j < size - 1; j++) {
            arr[j] = arr[j + 1];
        }
        // 更新元素数量
        size--;
        // 返回被删除的元素
        return num;
    }

    /* 列表扩容 */
    public void extendCapacity() {
        // 新建一个长度为原数组 extendRatio 倍的新数组，并将原数组复制到新数组
        arr = Arrays.copyOf(arr, capacity() * extendRatio);
        // 更新列表容量
        capacity = arr.length;
    }

    /* 将列表转换为数组 */
    public int[] toArray() {
        int size = size();
        // 仅转换有效长度范围内的列表元素
        int[] arr = new int[size];
        for (int i = 0; i < size; i++) {
            arr[i] = get(i);
        }
        return arr;
    }
}

2.4、小结

---

• 数组和链表是两种基本的数据结构，分别代表数据在计算机内存中的两种存储方式：连续空间存储和分散空间存储。两者的特点呈现出互补的特性。
• 数组支持随机访问、占用内存较少；但插入和删除元素效率低，且初始化后长度不可变。
• 链表通过更改引用（指针）实现高效的节点插入与删除，且可以灵活调整长度；但节点访问效率低、占用内存较多。常见的链表类型包括单向链表、环形链表、双向链表。
• 列表是一种支持增删查改的元素有序集合，通常基于动态数组实现。它保留了数组的优势，同时可以灵活调整长度。
• 列表的出现大幅提高了数组的实用性，但可能导致部分内存空间浪费。
• 程序运行时，数据主要存储在内存中。数组可提供更高的内存空间效率，而链表则在内存使用上更加灵活。
• 缓存通过缓存行、预取机制以及空间局部性和时间局部性等数据加载机制，为 CPU 提供快速数据访问，显著提升程序的执行效率。
• 由于数组具有更高的缓存命中率，因此它通常比链表更高效。在选择数据结构时，应根据具体需求和场景做出恰当选择。

2.5、习题

题目1：合并两个有序列表

leetcode链接：https://leetcode.cn/problems/merge-two-sorted-lists/description/?envType=study-plan-v2&envId=selected-coding-interview

题解1（迭代法）

解题思路：

1. 创建虚拟节点：创建一个虚拟链表dummy，并维护一个指针current指向这个虚拟链表
2. 比较两个链表的节点：同时遍历两个链表，比较当前节点的值，current指针指向较小的节点，链表头节点后移
3. 处理剩余的链表：如果比较完成之后，存在链表未比较的元素的链表，直接连接到current的后面即可！
4. 返回合并后的新链表：最后返回合并后的新链表的头节点

示例代码

/**
 * 合并两个有序链表（迭代法）
 * 
 * @param l1 链表 1
 * @param l2 链表 2
 * @return 合并后的链表
 */
public static ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    // 创建一个虚拟节点，作为合并后的链表的头节点
    ListNode dummy = new ListNode(-1);
    // 创建一个指针，指向合并后的链表的尾节点
    ListNode current = dummy;

****    // 遍历两个链表，比较节点值，将较小的节点添加到合并后的链表中
    while (l1 != null && l2 != null) {
        if (l1.val < l2.val) {
            current.next = l1;
            l1 = l1.next;
        } else {
            current.next = l2;
            l2 = l2.next;
        }
        current = current.next;
    }

    // 将剩余的节点添加到合并后的链表中
    current.next = l1 != null ? l1 : l2;

    return dummy.next; // 虚拟节点后的一个节点是新链表的头节点
}

题解2（递归法）

解题思路：

1. 递归终止条件：当一个链表为空时，直接返回另一个链表
2. 递归比较两个链表的头节点：
   • 如果l1.val <= l2.val，将l1作为当前节点，继续递归合并l1.next, l2
   • 否则，将l2作为当前节点，继续递归合并l1, l2.next
3. 返回当前节点：递归结束后，返回当前节点，作为合并后链表的头节点

示例代码

/**
 * 合并两个有序链表（递归法）
 * @param l1
 * @param l2
 * @return
 */
public static ListNode mergeTwoLists2(ListNode l1, ListNode l2){
    // 递归终止条件
    if (l1 == null) {
        return l2;
    } else if (l2 == null) {
        return l1;
    }

    // 递归调用
    if (l1.val <= l2.val) {
        l1.next = mergeTwoLists2(l1.next, l2); // 递归合并l1.next 和 l2
        return l1;
    }else{
        l2.next = mergeTwoLists2(l1, l2.next); // 递归合并l2.next 和 l1
        return l2;
    }
}