基于 ID3 算法的决策树概念+代码(R语言)+例子 -保姆级别手算教程

基于 ID3 算法的决策树 -Iterative Dichotomiser 3

Note: 本文侧重讲解ID3算法背后的原理以及如何使用，⭐ 想要了解ID3算法其背后原理的朋友阅读⭐。在很多平台中都有决策树的包，调用现成的包往往只需要一行代码就可以实现复杂的决策树，非常简单，固本文不再赘述。

ID3 概念

ID3算法是由Ross Quinlan基于奥卡姆剃刀理论（Occam’s razor）所设计的一种追求精简的决策树。该算法使用一种从上到下，从root 到leaf的贪心算法区分数据建立决策树。

算法

• 分类过程
  1. 计算数据中所有特征的information gain
  2. 设information gain最高的特征为决策点
  3. 根据决策点分割数据
  4. 用更新的数据重复这个过程
• 停止条件
  1. 分割数据后数据集中的特征都相同
  2. 没有剩余特征，所有特征都被使用过

判断最佳决策点

用来判断最佳决策点的方法有很多，包括：

Entropy,
Information gain,
Gini index,
Gain Ratio,
Reduction in Variance
Chi-Square
其中information gain是比较常用的一种基于Entropy的判断方法。

首先介绍Entropy 的概念

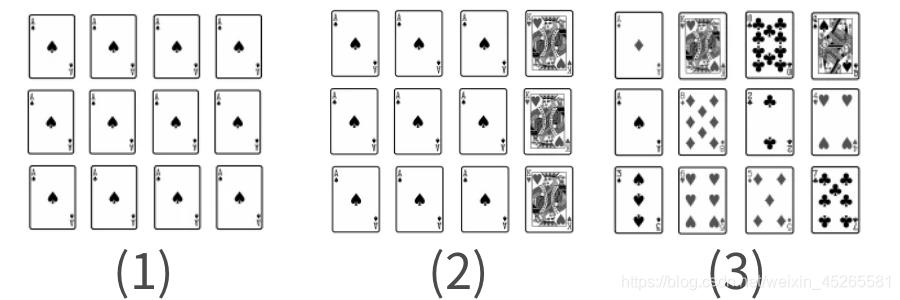
• Entropy可以理解为测量数据有多“不纯”(impurity)的指标，(1)比如一幅扑克牌中全都是黑桃A，我们就可以说这副牌非常的“纯”; (2)当全是黑桃A的扑克牌中混入红桃K后，这个数据集就不再单一，我们可以说这个数据集有一些“不纯”；(3)当这副扑克完全由不一样的牌组成时，数据集中没有相同的特征，我们所以我们可以称这样的情况为完全“不纯”。
  

• Entropy的公式

  • $$Entropy(n)=-\sum _{i=1}^c{p}_{i}lo{g}_2{p}_i$$
  • pi为每一个可能结果的概率

• Entropy 栗子🌰

  • 在一幅有52张牌的扑克里（没有王牌）随便抽一张特定花色特定数字的牌的概率为1/52
  • E n t r o p y ( n ) = − ∑ i = 1 52 1 52 l o g 2 1 52 = 5.7 Entropy(n) = - \sum_{i=1}^{52} \frac{1}{52}log_2\frac{1}{52} = 5.7 Entropy(n)=−i=1∑52<