LeetCode题库之树

原创已于 2022-09-27 11:03:58 修改 · 279 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

于 2022-09-27 11:01:36 首次发布

本文介绍了二叉树的基本概念及几种典型操作，包括生成二叉树的镜像、判断二叉树是否对称、从上到下打印二叉树及验证二叉搜索树的后序遍历结果。通过具体的实例和代码解释了每种操作的实现过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

树是一种递归的数据结构。二叉树是树的另一种树形结构，其特点是每个结点至多只有两棵子树( 即二叉树中不存在度大于2的结点)，并且二叉树的子树有左右之分，其次序不能任意颠倒。

下面定义树的类：

class TreeNode:
    def __init__(self,x):
        self.val = x  # 当前节点值
        self.left = None  # 左子树
        self.right = None  # 右子树

1.二叉树的镜像

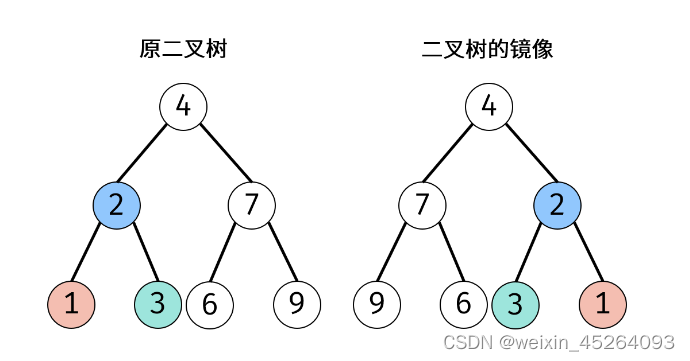
题目：请完成一个函数，输入一个二叉树，该函数输出它的镜像。

思路：从根节点开始，递归的对树进行遍历，从叶子节点先开始翻转得到镜像。如果当前遍历到的节点 $\textit{root}$ 的左右两棵子树都已经翻转得到镜像，那么我们只需要交换两棵子树的位置，即可得到以 $\textit{root}$ 为根节点的整棵子树的镜像。

步骤：（0）停止条件：根节点为空；(1)翻转根节点的左子树和右子树；(2)交换该根节点的左子树和右子树。

"""
示例 1：
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]
"""

def mirrorTree(root):
    if not root:
        return None
    left = mirrorTree(root.left)
    right = mirrorTree(root.right)
    root.left, root.right = right, left
    return root

2.对称的二叉树

题目：请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

思路：根据对称二叉树的定义，树中任意两个对称节点一定有:（1）对称节点值L=R；（2）L的左节点值=R的右节点值；（3）L的右节点值=R的左节点值。故，从顶到低进行递归，判断每对节点是否对称。递归停止条件：左右子树都为空。

"""
示例 1：
输入：root = [1,2,2,3,4,4,3]
输出：true
"""
def isSymmetic(root):
    def recur(L, R):
        "该函数可以用来判断左子树节点值是否等于右子树节点值。"
        if not L and not R:  # 递归停止条件
            return True
        if not L and not R or L.val != R.val:  # 不等，返回false
            return False
        return recur(L.left, R.right) and recur(L.right, R.left) # 对下一轮继续进行判断
    return recur(root.left, root.right) if root else True

3.从上到下打印二叉树

题目：从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。（相当于广度优先遍历）

思路：构造列表res用来存储打印的结构，使用队列queue来记录节点。停止条件：当前队列值为空。步骤：(1)当前节点不为空的话，就将其加入queue中；（2）删除当前节点，将节点值加入res中；（3）如果当前节点的左(右)不为空的话，就加入到queue中；(4)循环直到queue为空，停止。

"""
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
返回：
[3,9,20,15,7]
"""
def levelOrder(self, root):
    if not root:
        return []
    res, queue = [], collections.deque()
    queue.append(root)
    while queue:
        node = queue.popleft()
        res.append(node.val)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)
    return res

Ps:

C++和Python中使用队列的方式不一样。C++中队列是一种数据结构，直接定义就行。Python中需要导入包collections来加以引用。
Python 中使用 collections 中的双端队列 deque() ，其 popleft() 方法可达到 O(1) 时间复杂度；列表 list 的 pop(0) 方法时间复杂度为 O(N)。

4.二叉搜索树的后续遍历

二叉搜索树的特点：左子树的值 < 根节点，右子树的值 > 根节点。

题目：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

思路：递归分治的思想。利用二叉搜索树左子树、右子树、根节点的特性。相当于：递归+类似于二分法。

"参考以下这颗二叉搜索树：
     5
    / \
   2   6
  / \
 1   3

示例 1：
输入: [1,6,3,2,5]
输出: false"

def verifyPostorder(self, postorder: List[int]) -> bool:
    def recur(i, j):
        if i >= j:
            return True
        p = i
        # 根据大小关系找到左子树最后一个值对应的索引m
        while postorder[p] < postorder[j]:
            p += 1
            m = p
        while postorder[p] > postorder[j]:
            p += 1
        return p == j and recur(i, m-1) and recur(m, j-1)  # 到给定区间后就返回
    return recur(0, len(postorder) - 1)

树的具体内容见博客：数据结构：树(Tree)【详解】_UniqueUnit的博客-优快云博客_数据结构树

初学阶段，只是一个小笔记，其中所有的题目和题解都来源于LeetCode题库。