数据结构和算法简介
什么是程序设计?
所谓程序设计,即给出解决特定问题程序的过程,是软件构造活动中的重要组成部分。程序设计往往以某种程序设计语言为工具,给出这种语言下的程序。包括分析、设计、编码、测试、排错等不同阶段。
简单说起来就是数据结构(数据元素之间存在的一种或多种特定关系的集合)加上算法的集合
总说数据结构,那么数据结构有些什么样的结构呢
总的来说数据结构有两种逻辑结构(数据元素中的相互关系)和物理结构(数据的逻辑结构在计算机中的存储形式)
下面来介绍一下常见的四个逻辑结构
如下图
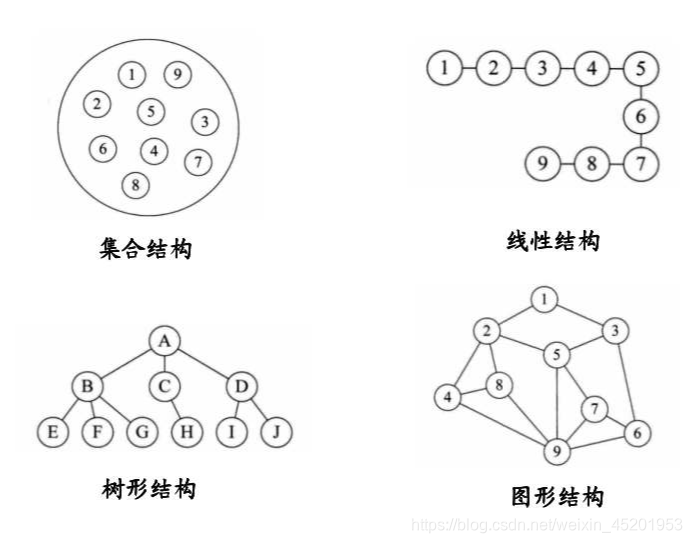
集合结构
集合结构其内的数据除了同属于一个集合外,之间没有其他关系。
从图中可以看到,每一个数据都是独立的,之间互不相关。
线性结构
线性结构中的元素是一一对应的关系。
在图中可见该结构中各个数据之间呈线性状一一排列,每个前驱数据指向该数据而后指向后继数据。
树形结构
数据元素之间存在一种一对多的关的层次关系。
树形结构中可以看到数据之间可以是一对一关系也可以是一对多关系。
图形结构
数据元素之间是多对多的关系。
图形结构中每个元素可以有多个元素与它对应。
物理结构
即如何把数据元素存储到计算机的存储器(针对内存而言,硬盘、软盘、光盘等外部存储器的数据组织通常用文件结构来描述)中。
说完了数据结构,我们来说说数据存储形式
数据存储形式有两种,顺序存储和链式存储。
顺序存储结构
把数据元素存放在地址连续的存储单元,他们之间的逻辑关系和物理关系是一致的。(例如数组的存放方式)
链式存储结构
把数据元素存放在任意的存储单元里面,这组存储单元可以是连续的,也可以是不连续的。
很明显,链式存储结构之间的数据存储关系要想反应其逻辑关系,就需要用到一个指针来存放数据元素的地址,通过地址找到相关联数据元素位置。
现在对数据结构有了一个了解,我们来看看算法
高斯的父亲作泥瓦厂的工头,每星期六他总是要发薪水给工人。在高斯三岁夏天时,有一次当他正要发薪水的时候,小高斯站了起来说:「爸爸,你弄错了。」然后他说了另外一个数目。原来三岁的小高斯趴在地板上,一直暗地里跟着他爸爸计算该给谁多少工钱。重算的结果证明小高斯是对的,这把站在那里的大人都吓的目瞪口呆。高斯常常带笑说,他在学讲话之前就已经学会计算了,还常说他问了大人字母如何发音后,就自己学着读起书来。
七岁时高斯进了St.Catherine小学。大约在十岁时,老师在算数课上出了一道难题:「把1到100的整数写下来,然后把它们加起来!」每当有考试时他们有如下的习惯:第一个做完的就把石板〔当时通行,写字用〕面朝下地放在老师的桌子上,第二个做完的就把石板摆在第一张石板上,就这样一个一个落起来。这个难题当然难不倒学过算数级数的人,但这些孩子才刚开始学算数呢!老师心想他可以休息一下了。但他错了,因为还不到几秒钟,高斯已经把石板放在讲桌上了,同时说道:「答案在这儿!」其他的学生把数字一个个加起来,额头都出了汗水,但高斯却静静坐着,对老师投来的,轻蔑的、怀疑的眼光毫不在意。考完后,老师一张张地检查着石板。
大部分都做错了,学生就吃了一顿鞭打。最后,高斯的石板被翻了过来,只见上面只有一个数字:5050(用不着说,这是正确的答案。)老师吃了一惊,高斯就解释他如何找到答案:1+100=101,2+99=101,3+98=101,……,49+52=101,50+51=101,一共有50对和为101的数目,所以答案是50×101=5050。由此可见高斯找到了算术级数的对称性,然后就像求得一般算术级数合的过程一样,把数目一对对地凑在一起。
从数学教高斯的故事中我们可以看出算法对程序设计有多么重要,他可以使得程序运行时间大大缩减。有些人可能会说,计算机运算速度那么快,算法真的有必要吗?答案是肯定的,虽然计算机运算速度很快,但是当面对海量数据时,暴力穷举的劣势就体现出来了,就像高斯的故事,如果把100换成一千万,可能计算机运算的那个时间里面人已经算出来了。因此,学习算法是程序设计的一个重要部分。
算法
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的优先序列,并且每条指令表示成一个或多个操作。
算法有五个基本特征:输入,输出,有穷性,确定性,可行性。
输入
算法至少具有零个或多个输入。(可以没有输入)
输出
算法至少具有一个或多个输出。(与输入不同,算法一定要有输出,可以使打印形式,也可以返回一个或者多个值。换句话说,程序是用来解决问题的,如果没有输出怎么解决问题)
有穷性
算法在执行完有限步骤后,自动结束而不会出现无限循环,每个步骤在可以接收时间内完成。
确定性
算法每一个步骤都有特定的含义,不会出现二义性。
算法在一定条件下,只有一条执行路径,相同的输入只能有唯一输出结果。
算法每个步骤应被精确定义而无歧义。
可行性
算法每一步都必须是可行的,每一步都能通过有限次数完成。
算法设计的要求
算法设计的要求大体上可以分为三个部分:正确性,可读性,健壮性。
正确性
- 正确性是指算法至少应该具有输入、输出和加工处理无歧义性,能正确反映问题需求,能得到问题的正确答案。
- 可粗略的分为四个层次
- 无语法错误
- 算法程序对于合法输入能够产生满足要求的输出
- 算法程序对于非法输入能够产生满足规格的说明
- 算法程序对于故意刁难的测试输入都有满足要求的输出结果
- 可粗略的分为四个层次
可读性
可读性是为了能够更加方便于阅读理解和交流,因为计算机的程序设计不是个人英雄主义的时代,需要团队的配合,同时可读性也可以方便自己日后对程序进行修改。
健壮性
当数据输入不合法时,算法能够做出相应的处理,而非产生异常,崩溃或莫名其妙的结果。
简单的说算法设计要求就是使时间效率尽量高,消耗的存储量尽量低。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








