机器学习练习题（2）+详细讲解

三。判断题
1.分类任务是预测连续值。（F）
2.回归任务是预测连续值。 （T）

解析：回归和分类属于机器学习中的有监督学习。分类任务是预测离散值，回归任务是预测连续值。

3.用线性代数的方式描述函数或者方程的好处之一是书写方便。 （T）

解析：现实生活中的数据比较复杂，尚且不完备。把他们拟合成一个函数或者方程，使用线性代数来描述他们是为了书写方便。

4，Σ是求和符号。（ T）
5.Π是求积符号。（T）
解析：这两个符号要记着，在机器学习中比较常见。

四。填空题。
1.在多元线性回归学习中，数据集用X表示，标签用y表示，模型参数用θ表示，那么其解析解公式是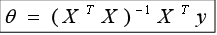
2.损失函数也叫 代价函数 或 目标函数
3.求函数机制的方法有两大类，分别是 解析解（闭式解） 和 数值解
4.numpy中求取平均值的函数是 mean，取标准差的函数是 std,取e的指数函数是 exp
5.sklearn用于线性回归器的类是SGDRegressor，其超参数中tol的作用是
设定一个判断梯度近似0的阈值。

知识点扩展：什么是梯度下降法？
梯度下降法分为批量梯度下降和随机梯度下降

思维引入：
什么是梯度？
梯度就是把每一个维度的偏导数集合在一起做一个向量。对于多元函数的θ，每次减去梯度值就能让多元损失函数朝着最佳解迈进一步

什么是下降？
负梯度这个向量构成的方向我们通常称为下降方向

梯度下降就是把每一个维度的偏导数集合在一个组合的一个向量按照负方向进行估测计算，从而找出最优的解。
（这只是我的个人见解）

批量梯度下降
%1.特点：每次求梯度的时候都需要做n次加和（假设有n个数据点）

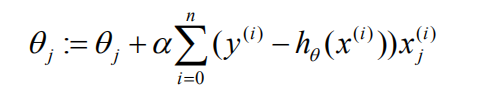
%2.优点：在每次迭代的时候都严格保证函数负梯度方向下降
%3.缺点：每次迭代运算量比较大，时间长

随机梯度下降

& 原始梯度下降需要通过全部样本计算负梯度方向
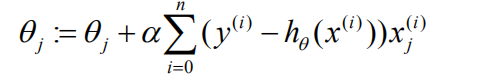& 随机梯度下降在计算负梯度时只选择一条数据或一部分数据进行运算
& 这样处理后，每次下降的方向不是严格意义上的损失函数的负梯度，会导致收敛次数增加
& 但是每次迭代的运算量大大减小了，在数据量很大的情况下仍然效率更高。

五。简答题。

1.解释一下什么是过拟合

答：过拟合就是模型对于训练集数据拟合的太过准确，以至于模型在与测试集进行拟合的时候出现的误差太大。

扩展：
过拟合出现的原因：抽取的数量比较小，观测到的特征少，在模型训练的过程中将训练集中的一些偶然现象做了规律。

怎样减少过拟合的情况呢？
降低模型的复杂度

2.什么是损失函数？损失函数的用途是什么？

答：损失函数用于评估y true 和y hat 之间差值的优良程度。

损失函数用于求最优解，一般是利用求导求出损失函数导函数，再利用数值解找到最小值，此时可以求出最优解

3.简述训练集合测试集数据的作用区别

答：训练集是在训练时刻使用，目的是求出最优解模型参数；
测试集是训练后测试时使用，目的是检测模型参数是否优良

六。程序题

1.梯度下降法中mse函数的求导过程。

（这个求导的过程在markdown中实在是不容易敲出来，所以我就放上了一张图片，大家见谅啊！(ૢ˃ꌂ˂ૢ) 其实我个人觉得公式记住就好了，至于推导嘛，这个面试中可能会有点用途(/ω＼)(/ω＼)）

2.随机梯度下降法编码

%1.设置超参
learning_rate=0.001 学习率
n_iterator=1000 迭代次数
tol=0.000001 设定一个梯度是否近似于0的阈值

%2.随机初始化参数

theta=np.random.uniform(0,1,size=(2,1))

%3.打乱索引值

index=np.arange(m)
np.random.shuffle(m)




%4.开始迭代

for i inrange（n_itertor）:
for j in range(m):
#随机选择一个样本
xi=X[index[j]]
yi=y[index[j]]
#计算当前的梯度
gradients=xi.T.dot(xi.dot(theta)-yi)
#沿着负梯度方向更新 theta
theta=theta-learning_rate*gradients
#判断当前梯度是否近似0，如果是则退出，表示已经求出最好的模型；
if np.abs(gradients[0][0]<tol and np.abs(gradients[1][0])<tol):
break
print(theta)