指数平滑方法简介

本文链接：个人站 | 简书 | 优快云
版权声明：除特别声明外，本博客文章均采用 BY-NC-SA 许可协议。转载请注明出处。

指数平滑（Exponential smoothing）是除了 ARIMA 之外的另一种被广泛使用的时间序列预测方法（关于 ARIMA，请参考 时间序列模型简介）。 指数平滑即指数移动平均（exponential moving average），是以指数式递减加权的移动平均。各数值的权重随时间指数式递减，越近期的数据权重越高。常用的指数平滑方法有一次指数平滑、二次指数平滑和三次指数平滑。

1. 一次指数平滑

一次指数平滑又叫简单指数平滑（simple exponential smoothing， SES），适合用来预测没有明显趋势和季节性的时间序列。其预测结果是一条水平的直线。模型形如：

Forecast equation: ${\hat{y}}_{t+h|t}=l_t$
Smoothing equantion: $l_t=\alpha y_t+(1-\alpha )l_{t-1}$

其中 $y_t$ 是真实值，${\hat{y}}_{t+h}(h\in Z^{+})$ 为预测值，$l_t$ 为平滑值， $0<\alpha <1$。

定义残差 ${ϵ}_t=y_t-{\hat{y}}_{t|t-1}$，其中 $t=1,\cdots ,T$，则可以通过优化方法得到 $\alpha$ 和 $l_0$。

$$({\alpha }^{\ast },l_0^{\ast })=\underset{(\alpha ,l_0)}{\min }\sum _{t=1}^T{ϵ}_t^2=\underset{(\alpha ,l_0)}{\min }\sum _{t=1}^T{\left(y_t-{\hat{y}}_{t|t-1}\right)}^2$$

使用 python 的 statsmodels 可以方便地应用该模型：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import SimpleExpSmoothing

x1 = np.linspace(0, 1, 100)
y1 = pd.Series(np.multiply(x1, (x1 - 0.5)) + np.random.randn(100))
ets1 = SimpleExpSmoothing(y1)
r1 = ets1.fit()
pred1 = r1.predict(start=len(y1), end=len(y1) + len(y1)//2)

pd.DataFrame({
   
   
    'origin': y1,
    'fitted': r1.fittedvalues,
    'pred': pred1
}).plot(legend=True)

效果如图：

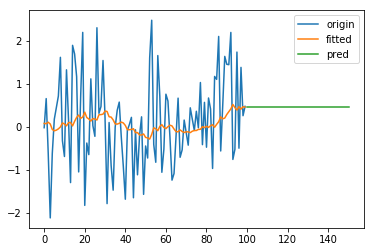
2. 二次指数平滑

2.1 Holt’s linear trend method

Holt 扩展了简单指数平滑，使其可以用来预测带有趋势的时间序列。直观地看，就是对平滑值的一阶差分（可以理解为斜率）也作一次平滑。模型的预测结果是一条斜率不为0的直线。模型形如：

Forecast equation: ${\hat{y}}_{t+h|t}$