动态规划分析-优快云博客

该博客主要介绍了如何运用动态规划算法解决0-1背包问题，给出了具体的Java代码实现，通过创建背包表和额外的标志表来确定最优解及所包含的商品。在保证背包容量的情况下，找到能获得最大价值的商品组合。

在这里插入图片描述

package suanfa10;

public class Beibao {
    public static void main(String[] args) {
        //假设有三个商品, 设置两个数组分别存放它们的重量和价格, 前面加0是为了方便商品的编号和下标对应
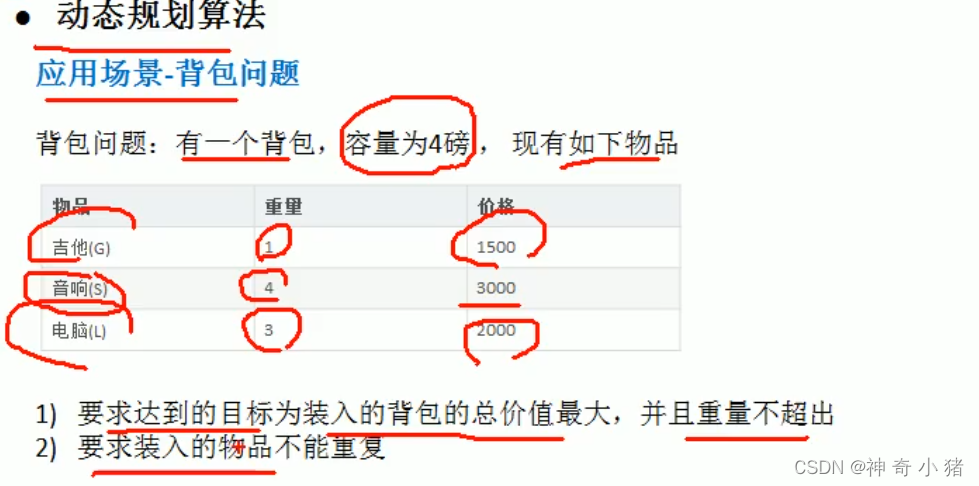
        int[] w = {0, 4, 3, 1};  //一号商品的重量4磅
        int[] v = {0, 3000, 2000, 1500}; //一号商品的价格是3000元
        int num = 3; //商品的数量是3
        int bagVal = 4; //背包的容量是4磅

        //创建一张背包表, 用动态规划解决背包问题
        int[][] bagbiao = new int[num+1][bagVal+1];
        //创建一张大小和背包表一样的表用来判断哪些商品放入了背包
        int[][] pagage = new int[num+1][bagVal+1];

        //表的第一行和第一列初始化为0
        for (int i = 0; i <= bagVal; i++){
            bagbiao[0][i] = 0;
        }
        for (int i = 0; i <= num; i++){
            bagbiao[i][0] = 0;
        }

       /* //动态规划
        for (int i = 1; i <= num; i++){
            for (int j = 1; j <= bagVal; j++){
                if (j < w[i]){
                    bagbiao[i][j] = bagbiao[i-1][j];
                }else{
                    bagbiao[i][j] = Math.max(bagbiao[i-1][j], bagbiao[i-1][j-w[i]]+v[i]);  //这样一来就确保每个各子都是最优解
                }
            }
        }*/
       //以上的写法虽然能得到最后背包中最优解的价格, 却不能知道放入了哪些商品

        for (int i = 1; i <= num; i++){
            for (int j = 1; j <= bagVal; j++){
                if (j < w[i]){
                    bagbiao[i][j] = bagbiao[i-1][j];
                }else{
                    //bagbiao[i][j] = Math.max(bagbiao[i-1][j], bagbiao[i-1][j-w[i]]+v[i]);  //这样一来就确保每个各子都是最优解
                    if(bagbiao[i-1][j] < bagbiao[i-1][j-w[i]]+v[i]){
                        bagbiao[i][j] = bagbiao[i-1][j-w[i]]+v[i];
                        pagage[i][j] = 1; //表示第i号商品可以放进此时容量为j的包
                    }else{
                        bagbiao[i][j] = bagbiao[i-1][j];
                    }
                }
            }
        }

        //从后面开始操作pagage表就可以知道哪些东西放进了包, 而且可以防止数据冗余
        int i = pagage.length-1;
        int j = pagage[0].length-1;
        while(i > 0 && j > 0){
            if (pagage[i][j] == 1){
                System.out.printf("将%d号商品放进了包\n", i);
                j = j - w[i];
            }
            i --;
        }

    }

}

将3号商品放进了包
将2号商品放进了包