Data Mining 2复习笔记2 - Ensembles

2. Ensembles

Ensembles: wisdom of the crowds for learning operators instead of asking a single learner, combine the predictions of different learners

Prerequisites for ensembles: accuracy and diversity
Accuracy: different learning operators can address a problem
Diversity: different learning operators make different mistakes
That means: predictions on a new example may differ. If one learner is wrong, others may be right.
Ensemble learning: use various base learners, combine their results in a single prediction.

2.1 Voting

The most straight forward approach
classification: use most-predicted label
regression: use average of predictions

We have already seen this: k-nearest neighbors(KNN), each neighbor can be regarded as an individual classifier

Why does Voting Work?

In theory, we can lower the error infinitely just by adding more base learners
But that is hard in practice. Reason: The formula only holds for independent base learners. It is hard to find many truly independent base learners at a decent level of accuracy

2.2 Bagging

Biases in data samples may mislead classifiers: overfitting problem (model is overfit to single noise points)

If we had different samples, e.g., data sets collected at different times, in different places, …and trained a single model on each of those data sets… Only one model would overfit to each noise point, so voting could help address these issues.
But usually, we only have one dataset!

Bagging operator uses a base learner

Bagging can ensure diversity as different rule models are learned.

Variant of Bagging: Randomization
Randomize the learning algorithm instead of the input data
Some algorithms already have a random component, e.g. initial weights in neural net.
Most algorithms can be randomized, e.g., greedy algorithms: Pick from the N best options at random instead of always picking the best options, e.g.: test selection in decision trees or rule learning.
Can be combined with bagging

Random Forests
A variation of bagging with decision trees
Train a number of individual decision trees, each on a random subset of examples & only analyze a random subset of attributes for each split.(Recap: classic DT learners analyze all attributes at each split)

Usually, the individual trees are left unpruned. 不对单独的决策树进行剪枝
Reason: Unpruned trees in Random Forests contribute to the model’s overall strength by increasing diversity and complexity, which are key to the effectiveness of ensemble methods. The robustness of the aggregation process in Random Forests mitigates individual tree overfitting, leading to better generalization and performance. Additionally, leaving trees unpruned simplifies the algorithm and speeds up the training process, making it a practical choice that aligns with empirical observations of high performance.

Paradigm Shift: Many Simple Learners
Bagging allows a different approach(several simple models instead of a single complex one)
Analogy: the SPIEGEL poll (mostly no political scientists, nevertheless: accurate results)
Extreme case: using only decision stumps
Decision stumps: decision trees with only one node
决策桩（decision stumps）是指只包含一个节点的决策树。这样的树仅进行一次分裂，通常基于单个特征的某个阈值进行判断，从而将数据集分成两个子集。由于决策桩非常简单，因此它们往往不足以捕获复杂的数据关系，但在某些情况下，它们可以作为基本的学习器来构建更复杂的集成模型，比如AdaBoost。在AdaBoost算法中，决策桩通常被用作弱分类器，多个决策桩的组合可以形成一个更强大的分类器。

Bagging with Weighted Voting
Some learners provide confidence values, e.g., decision tree learners, Naive Bayes

Weighted voting
use those confidence values for weighting the votes
some models may be rather sure about an example, while others may be indifferent

Python: parameter voting=soft
sums up all confidences for each class and predicts argmax
caution: requires comparable confidence scores!

2.3 Intermezzo: Learning with Weighted Instances

Weighted instances: assign each instance a weight (think: importance). Getting a high-weighted instance wrong is more expensive
accuracy etc. can be adapted

Example:
Data collected from different sources (e.g., sensors). Sources are not equally reliable - we want to assign more weight to the data from reliable sources

Two possible strategies of dealing with weighted instances

1. Changing the learning algorithm
   e.g., decision trees, rule learners: adapt splitting/rule growing heuristics
2. Duplicating instances
   an instance with weight n is copied n times
   simple method that can be used on all learning algorithms

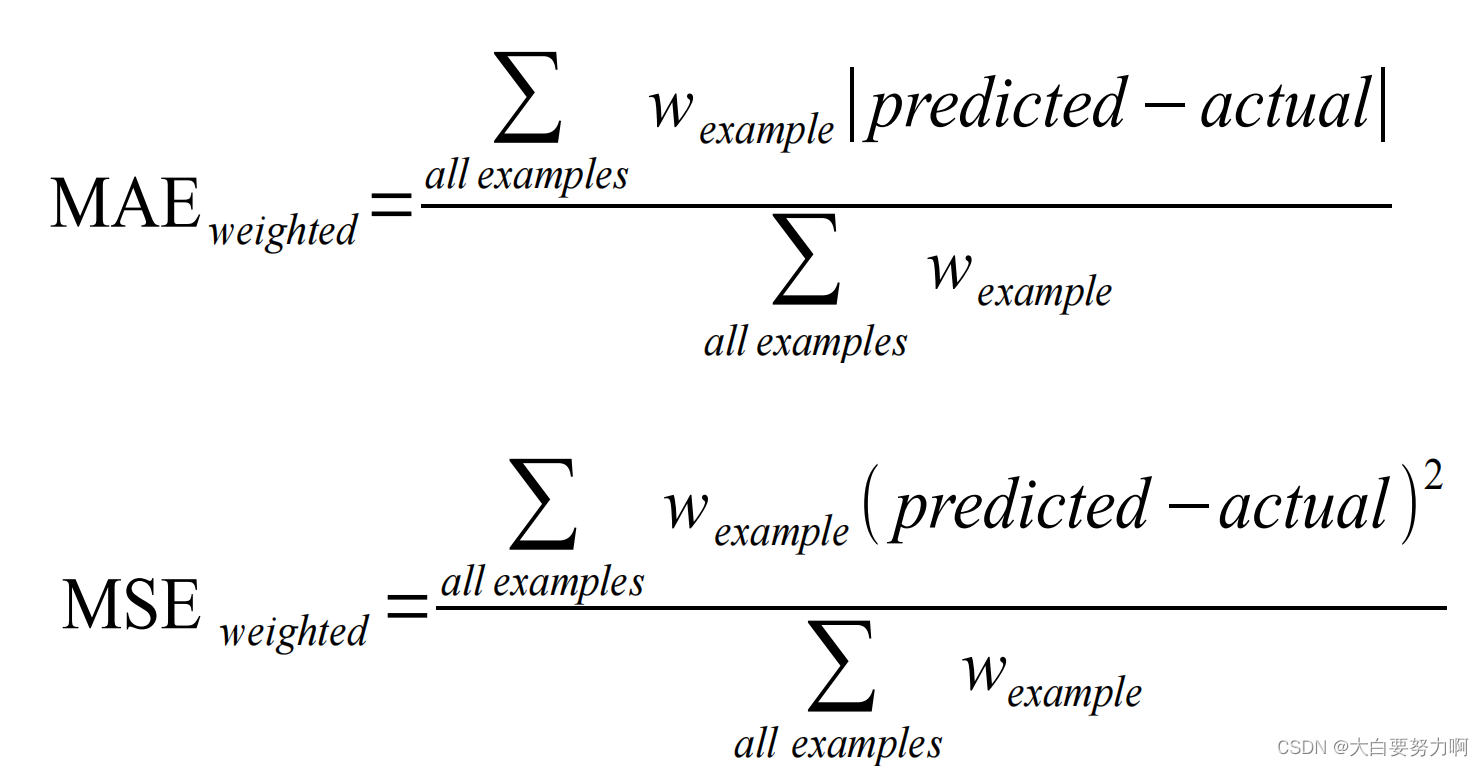
Accuracy

Accuracy with Weights

Adapting Algorithms: Decision Trees
Gini index as splitting criterion
The probabilities are obtained by counting examples. Again, we can sum up weights instead. The same works for rule-based classifiers and their heuristics.

Adapting Algorithms: Neural Networks

Adapting Algorithms: k-NN
Standard approach: use average of neighbor predictions
With weighted instances: weighted average

Handling imbalanced classification problems
So far:

1. undersampling
   removes examples → loss of information
2. oversampling
   adds examples → larger data (performance!)
3. synthetic data points (SMOTE)
4. Alternative:
   • lowering instance weights for larger class. Simplest approach: weight 1/|C| for each instance in class C
     Reason: Balance the Influence of Classes & Improve Performance on Minority Class & Mitigate Class Imbalance

2.4 Boosting

Idea of boosting: Train a set of classifiers, one after another. Later classifiers focus on examples that were misclassified by earlier classifiers, weight the predictions of the classifiers with their error

Realization:

1. perform multiple iterations
   each time using different example weights
2. weight update between iterations: increase the weight of incorrectly classified examples -> so they become more important in the next iterations (misclassification errors for these examples count more heavily)
3. combine results of all iterations
   weighted by their respective error measures

Boosting 算法首先训练一个基本分类器，然后根据之前分类器的表现来调整数据集，使得下一个分类器更加关注之前分类器错误分类的样本。
调整样本权重：在每次训练新分类器时，Boosting 算法会调整数据集的样本权重，使得之前被错误分类的样本在下一轮训练中更有可能被正确分类，从而提高整体的预测性能。
加权组合预测结果：最后，Boosting 算法将每个分类器的预测结果按照其性能进行加权组合，通常是通过投票或加权平均的方式，从而得到最终的集成模型。
在组合预测结果时，通常会根据每个分类器的错误率来给予其不同的权重。错误率低的分类器会被赋予更高的权重，以便它们对最终的预测结果产生更大的影响。这样做可以提高整体的预测性能，并减少集成模型的偏差。

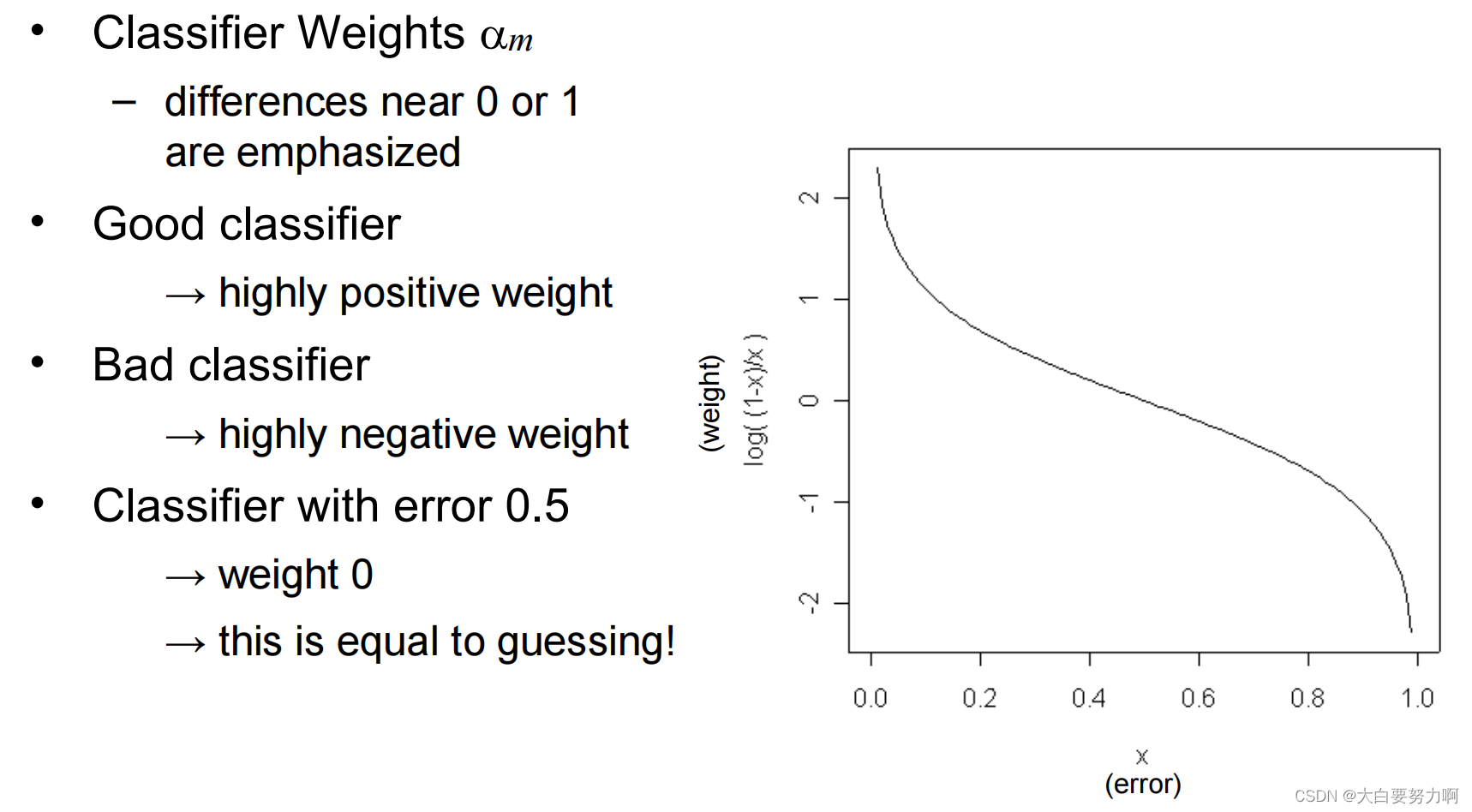
Illustration of the Weights

在一些集成学习算法中，如 AdaBoost，每个基本分类器都会被赋予一个权重，该权重反映了该分类器对最终预测的贡献程度。这些权重通常会根据分类器的性能来调整，使得表现良好的分类器被赋予更高的权重，而表现较差的分类器则被赋予较低的权重。

如果一个分类器的性能非常好，那么它的权重会是一个非常正的数值，接近1。这表示该分类器在最终预测中会有很大的影响力。

相反，如果一个分类器的性能很差，那么它的权重会是一个非常负的数值，接近-1。这表示该分类器的预测结果可能会被反转，以提高整体的预测性能。

如果一个分类器的错误率为0.5，意味着它的预测效果等同于随机猜测，因此它的权重会接近0。这样做的目的是尽可能地降低它对最终预测的影响，因为它的预测结果不具有任何信息性。

Example

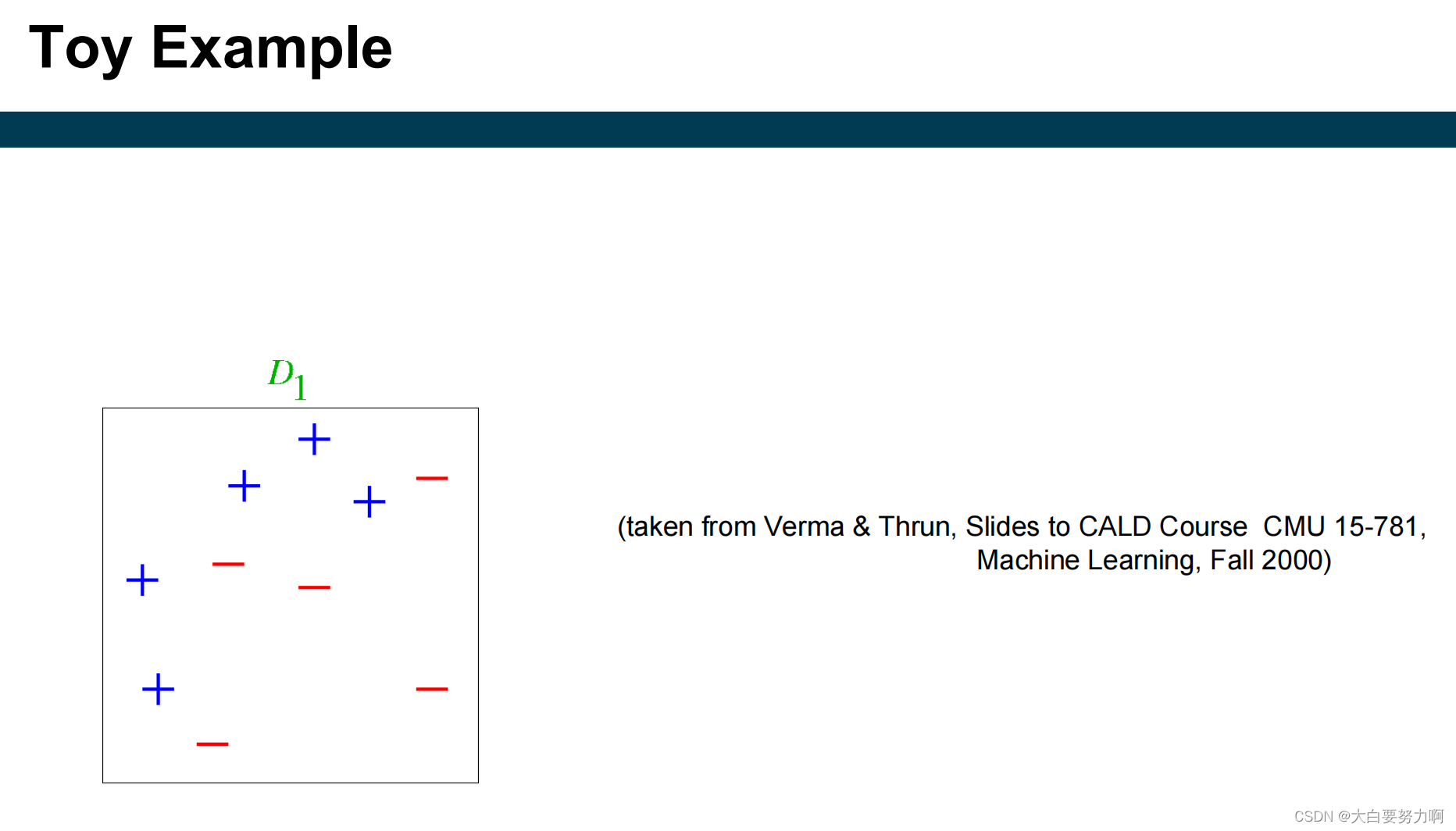
Hypothesis Space of Ensembles
Each learner has a hypothesis space. e.g., decision stumps: a linear separation of the dataset, parallel to the axes.
假设空间（Hypothesis Space）是指机器学习模型能够表示的所有可能的解的集合。在监督学习中，假设空间通常由模型的参数空间决定，它描述了模型所能够学习的所有可能的函数或决策规则。具体来说，假设空间包含了模型能够根据给定的输入数据进行预测的所有可能的函数或者概念。例如，在线性回归中，假设空间由所有可能的线性函数组成；在决策树中，假设空间由所有可能的决策树结构组成；在神经网络中，假设空间由所有可能的网络结构和参数组合组成。

The hypothesis space of an ensemble can be larger than that of its base learners. 当将多个基本学习器组合成一个集成时，集成的假设空间可能会比单个基本学习器的假设空间更大。这是因为每个基本学习器可以对数据集进行不同的划分，从而形成不同的线性划分。因此，集成学习的假设空间可以包含单个基本学习器所能表示的所有线性划分，以及更多其他划分方式，例如多边形划分。
Example: bagging with decision stumps
different stumps → different linear separations
resulting hypothesis space also allows polygon separations

Ensembles have been used to improve generalization accuracy on a wide variety of problems. On average, Boosting provides a larger increase in accuracy than Bagging.
–> Boosting on rare occasions can degrade accuracy
–> Bagging more consistently provides a modest improvement
Boosting is particularly subject to over-fitting when there is significant noise in the training data because subsequent learners over-focus on noise points

Voting
each ensemble member votes for one of the classes and predict the class with the highest number of vote (e.g., bagging)

Weighted Voting
make a weighted sum of the votes of the ensemble members, weights typically depend
-on the classifier’s confidence in its prediction (e.g., the estimated probability of the predicted class)
-on error estimates of the classifier (e.g., boosting)

Stacking
Why not use a classifier for making the final decision?
Training material are the class labels of the training data and the
(cross-validated) predictions of the ensemble members

2.5 Stacking

Basic Idea: learn a function that combines the predictions of the individual classifiers.

Stacking and Overfitting
Consider a dumb base learner D, which works as follows: during training: store each training example; During classification: if example is stored, return its class. Otherwise, return a random prediction.
If D is used along with a number of classifiers in stacking, what will the meta classifier look like?
D is perfect on the training set, so the meta classifier will say: always use D’s result.

Solution 1: split dataset (e.g., 50/50)
use one portion for training the base classifiers
use other portion to train meta model
Solution 2: cross-validate base classifiers
train classifier on 90% of training data
create features for the remaining 10% on that classifier
repeat 10 times

The second solution is better in most cases
uses whole dataset for meta learner & uses 90% of the dataset for base learners

Variant 1: keep the original attributes
Predictions of base learners are additional attributes for the stacking predictor – allows the identification of “blind spots” of individual base learners

Variant 2: stacking with confidence values
If learners output confidence values, those can be used by the stacking learner. Often further improves the results.

2.6 Regression Ensembles

Most ensemble methods also work for regression

• voting: use average
• bagging: use average or weighted average
• stacking: learn regression model as stacking model!
• boosting: the regression variant is called additive regression

2.6.1 Additive Regression

Boosting can be seen as a greedy algorithm for fitting additive models
Same kind of algorithm for numeric prediction:

• Build standard regression model
• Gather residuals, learn model predicting residuals, and repeat
  Given a prediction p(x), residual = (x-p(x))²

To predict, simply sum up weighted individual predictions from all models

Additive Regression w/ Linear Regression
What happens if we use Linear Regression inside of Additive Regression?
The first iteration learns a linear regression model lr1 by minimizing the sum of squared errors
The second iteration aims at learning a LR lr2 model for x’ = (x-lr1(x))² Since (x-lr1(x))² is already minimal, lr2 cannot improve upon this
Hence, the subsequent linear models will always be a constant 0

在加法回归中，第二次迭代得到的线性模型 lr2 会试图对第一次迭代的残差进行建模，即学习一个模型来最小化残差的平方。然而，由于第一次迭代已经最小化了残差，因此第二次迭代的模型 lr2 将无法进一步减小这个残差。因此，第二次迭代得到的线性模型 lr2 将是一个全零的模型，因为无论如何调整 lr2，它都无法对残差进行更多的优化。因此，lr2 将始终学习到一个恒定的值，即常数0。

additive and linear regression are not a good match

2.6.2 XGBoost

A pretty strong learning algorithm: Additive Regression w/ Regression Trees
Regularization: Respect size of trees & Larger trees: more likely to overfit!(Introduce penalty for tree size) & Overcomes the problem of overfitting in boosting

Intermediate Recap
Ensemble methods

• outperform base learners
• help minimizing shortcomings of single learners/models
• simple and complex methods for method combination

Reasons for performance improvements

• individual errors of single learners can be “outvoted”
• more complex hypothesis space

Ensembles for Other Problems
Clustering: trying to unify different clusterings & using a consensus function mapping different clusterings to each other

Outlier detection: unifying outlier scores of different approaches & requires score normalization and/or rank aggregation

2.7 Learning with Costs

Most classifiers aim at reducing the number of errors (all errors are regarded as being equally important)
In reality, misclassification costs may differ
Consider a warning system in an airplane. Issue a warning if stall is likely to occur based on a classifier using different sensor data. Wrong warnings may be ignored by the pilot. Missing warnings may cause the plane to crash. Here, we have different costs for
actual: true, predicted: false → very expensive
actual: false, predicted true → not so expensive

2.7.1 MetaCost Algorithm

Form multiple bootstrap replicates of the training set, learn a classifier on each training set, i.e., perform bagging -> Estimate each class’s probability for each example by the fraction of votes that it receives from the ensemble -> Use conditional risk equation to relabel each training example with the estimated optimal class -> Reapply the classifier to the relabeled training set

2.7.2 MetaCost vs. Balancing

Balancing
In an unbalanced dataset, there is a bias towards the larger class. Balancing the dataset helps building more meaningful models.

MetaCost
Incidentally unbalance the dataset, labeling more instances with the “cheap” class. Make the learner have a bias towards the “cheap” class, i.e., expensive mis-classifications are avoided in the end, the overall cost is reduced.

In the example:
There will be more false alarms (stall warning, but actually no stall), the risk of not issuing a warning is reduced

2.8 Summary