探究动态规划

动态规划是多阶段决策最优解模型<自下而上求每个问题的最优解>

三要素

• 最优子结构
• 状态转移方程
• 重叠子问题

例

1.以斐波那契数列问题为例：

采用递归的思路，自上而下

public static int fibonacci(int n) {
    if (n == 1) return1;
    if (n == 2) return2;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

改用自底向上的方式来递推，即动态规划

public int f(int n) {
    if (n == 1) return1;
    if (n == 2) return2;
    int result = 0;
    int pre = 1;
    int next = 2;
    
    for (int i = 3; i < n + 1; i ++) {
        result = pre + next;
        pre = next;
        next = result;
    }
    return result;
}

2.以三角形最短路径为例

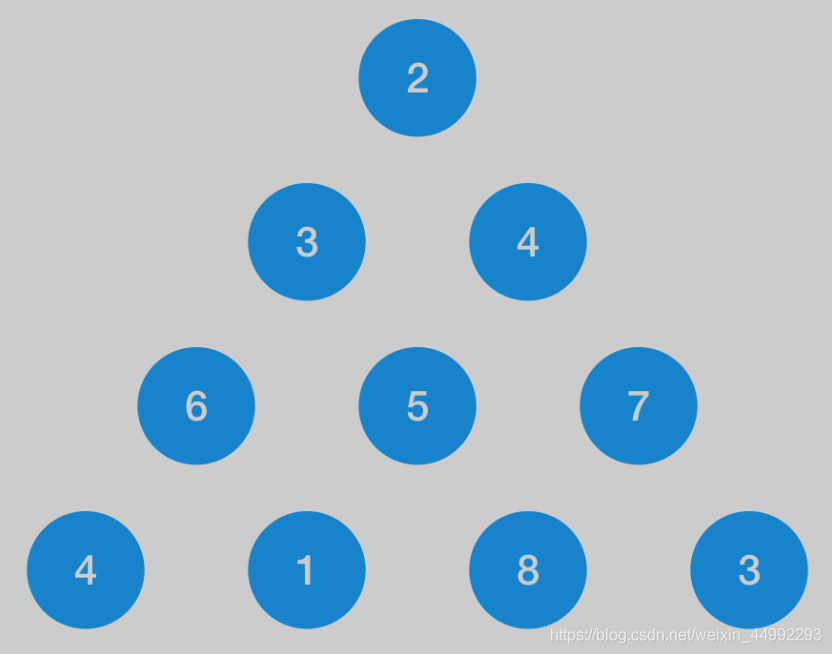
可用递归来解

private static int[][] triangle = {
            {2, 0, 0, 0},
            {3, 4, 0, 0},
            {6, 5, 7, 0},
            {4, 1, 8, 3}
    };
    
    public static int traverse(int i, int j) {
        //以递归方式求解
        int totalRow = 4; // 总行数
        if (i >= totalRow - 1) {
            return 0;
        }
        // 往左下节点走时
        int leftSum = traverse(i + 1, j) + triangle[i + 1][j];
        // 往右下节点走时
        int rightSum = traverse(i + 1, j + 1) + triangle[i + 1][j + 1];
        // 记录每个节点往左和往右遍历的路径和的最小值
        return Math.min(leftSum, rightSum);
    }

递归的思路是，自上而下将每个元素的最优解求出来

但在递归的过程中有大量重复的子问题。

改用自下而上的方式，即动态规划

对于最底层，他们对应的最短路径即他们本身

对于倒数第二层，他们对应的最短路径即本身加他们对应的两个子元素的较小值，将自身的值改为本身的值+子元素的较小值

对于倒数第三层，对应的最短路径，即本身加对应的两个子元素较小值，将自身的值改为本身的值+子元素的较小值

…

…

DP状态转移方程：
DP[i,j] = min(DP[i+1, j], D[i+1, j+1]) + triangle[i,j]

private static int[][] triangle = {
            {2, 0, 0, 0},
            {3, 4, 0, 0},
            {6, 5, 7, 0},
            {4, 1, 8, 3}
    };
public static int traverseDP() {
        int ROW = 4;
        //记录每一行的每个元素的最优解
        int[] mini = triangle[ROW - 1];
        // 从倒数第二行求起，因为最后一行的值本身是固定的
        for (int i = ROW - 2; i >= 0; i--) {
            for (int j = 0; j < triangle[j].length; j++) {
                mini[j] = triangle[i][j] + Math.min(mini[j], mini[j+1]);
            }
        }
        return mini[0];
}

3.以凑零钱问题为例

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。输入: coins = [1, 2, 5], amount = 11，输出: 3 解释: 11 = 5 + 5 + 1输入: coins = [2], amount = 3，输出: -1

以递归方式解题

每颗硬币对应的最优解

f(amounts,coins)=f(amount - coins[i]) + 1；

public static int recursion(int target,int []coins){
        if (target == 0) {
            return 0;
        }

        if (target < 0) {
            return -1;
        }

        int result = Integer.MAX_VALUE;
        for (int i=0;i<coins.length;i++){
            int temp=recursion(target-coins[i],coins);
            if (temp==-1) continue;
            result=Math.min(temp+1,result);
        }
        if (result== Integer.MAX_VALUE){
            return -1;
        }
        return result;
    }

有大量的重复子问题，运用动态规划解

DP[i] = min{ DP[ i - coins[j] ]} + 1

思路是从求从1到target的每个值的最优解，

public static int dp(int target,int []coins){
        int []dp=new int[target+1];
        for (int i=0;i<dp.length;i++){
            dp[i]=target+1;
        }
        dp[0]=0;
        for (int i=1;i<dp.length;i++){
            for (int j=0;j<coins.length;j++){
                if (i>=coins[j]){
                    dp[i]=Math.min(dp[i-coins[j]],dp[i])+1;
                }
            }
        }
        if (dp[target]==target+1){
            return -1;
        }
        return dp[target];
    }

DP代码解析：
首先定义一个名叫dp的数组，每个元素存储的是对应下标的最优解，例如dp[3]存储的是3元的最优解。

通过双层循环：

• 外层循环是将dp每个元素遍历一次，每次遍历求得dp的值
• 内层循环是遍历coins数组，当i（即这次外循环的目标钱）大于coins[j]时，求dp[i-coins[j]]，与之前求得的的dp[i]作比较，取较小值，+1（+1的意义是使用了这枚硬币）。内层循环结束，就能得出dp[i]，也就是说是使用哪枚硬币能有最优解。

当dp[target]的值经过了两层循环都没改变时，说明没有对应的硬币组合，返回-1。

总结

动态规划一般是自下而上的， 通过状态转移方程自下而上的得出每个子问题的最优解（即最优子结构），最优子结构其实也是穷举了所有的情况得出的最优解，得出每个子问题的最优解后，也就是每个最优解其实是这个子问题的全局最优解，这样依赖于它的上层问题根据状态转移方程自然而然地得出了全局最优解

参考自：

时，说明没有对应的硬币组合，返回-1。

总结

动态规划一般是自下而上的， 通过状态转移方程自下而上的得出每个子问题的最优解（即最优子结构），最优子结构其实也是穷举了所有的情况得出的最优解，得出每个子问题的最优解后，也就是每个最优解其实是这个子问题的全局最优解，这样依赖于它的上层问题根据状态转移方程自然而然地得出了全局最优解

参考自：

https://mp.weixin.qq.com/s?__biz=MzI2NjA3NTc4Ng==&mid=2652082022&idx=2&sn=d785c0d1664b428e2548b42b69862562&key=1fb38d1ad08361bbcc2d5bdaa7867e959c5ce0879f0704d410bbcc06de2f1345b9c135b1eb3a1bc315c109400492fae994d22cf4d1c81bcf098e1245e2f8385e4e4c32522b374da274abedda46996ec7&ascene=1&uin=NDM3NTQ3NzUw&devicetype=Windows+10+x64&version=6209007b&lang=zh_CN&exportkey=Ayl1lvnF3RgFMlICpngjal4%3D&pass_ticket=3LQhlD2AX3v3r78mIiYjgTn%2BkrGc91ysaimvXEpP8mE7xAAoiKt17MANEaypAuEl