机器学习之八大算法⑤——支持向量机(SVM算法)

SVM算法代码及注释

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris		#鸢尾花数据集
from sklearn.svm import SVC
import warnings

# 消除警告
warnings.filterwarnings('ignore')

# 数据读取
data = load_iris()      #调用鸢尾花数据集：150个数据，4个特征，3个类别用0,1,2
x = data.data           #获取特征值
y = data.target         #获取实际y值

# 选取特征和类别
x = x[y!=2,1:3]     #特征0,1,2,3   1:3是表示的第2个特征和第3个特征
y = y[y!=2]			#实际值0,1，2   选取y不等于2的值

# 洗牌
np.random.seed(7)						#声明种子
order = np.random.permutation(len(x))
x = x[order]
y = y[order]

#特征缩放(标准化)
x -= np.mean(x,0)
x /= np.std(x,0,ddof=1)

# 切分
train_x,test_x = np.split(x,[int(0.7*len(x))])		#第二个参数要是整型
train_y,test_y = np.split(y,[int(0.7*len(x))])

#构建模型
model = SVC(C=1.0,kernel='linear')		#kernel:核函数， ‘linear’(线性), ‘poly’(多项式), ‘rbf’(高斯), ‘sigmoid’等， (default='rbf')
model.fit(train_x,train_y)

print('训练集准确率:',model.score(train_x,train_y))
print('测试集准确率:',model.score(test_x,test_y))
print('测试集预测结果:',model.predict(test_x))
print('支持向量索引：',model.support_)
print('支持向量的个数：',model.n_support_)
print('theta：',model.coef_)                 # 权重，仅适用于线性核函数


#画图
#指定画布范围
minx1,maxx1 = np.min(x[:,0]),np.max(x[:,0])
minx2,maxx2 = np.min(x[:,1]),np.max(x[:,1])

#把画布分成200*200的网格
x1,x2 = np.mgrid[minx1:maxx1:200j,minx2:maxx2:200j]

#计算网格中心到超平面的距离
x1x2 = np.c_[x1.ravel(),x2.ravel()]    #(40000, 2)  把x1,x2拼接成(40000, 2) 的矩阵

z = model.decision_function(x1x2)      #(200,)  把x1x2到决策边界的值算出来分出正负   
z = z.reshape(x1.shape)				   #(200,200) 还原到原来网格200*200 

#画训练集的样本图
plt.scatter(x[:,0],x[:,1],c=y,cmap=plt.cm.Paired,edgecolors='k',zorder=10)

#画测试集样本图
# edgecolors='k'边框为黑色；facecolor='none'不给样本填充颜色
plt.scatter(test_x[:,0],test_x[:,1],s=100,cmap=plt.cm.Paired,edgecolors='k',zorder=10,facecolor='none')

#画等值面
plt.contourf(x1,x2,z>=0,cmap=plt.cm.Paired)

#画等值线
plt.contour(x1,x2,z,levels=[-1,0,1],linestyles=['--','-','--'],colors=['r','g','b'])
plt.show()

效果展示

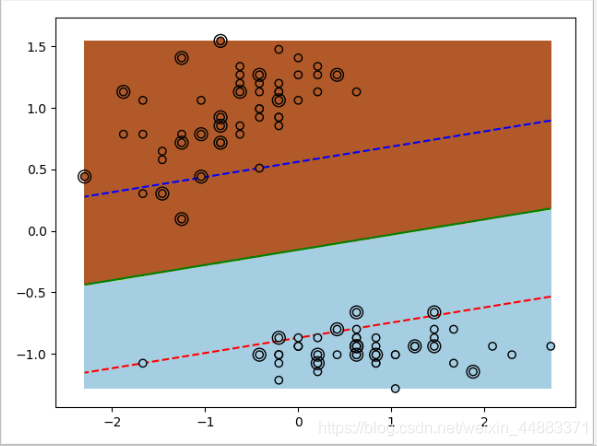
SVM算法python库实现:

clf = svm.SVC(C=0.1, kernel=‘linear’, decision_function_shape=‘ovr’)
主要参数：

C: 惩罚参数， (default=1.0)

kernel: 核函数， ‘linear’(线性), ‘poly’(多项式), ‘rbf’(高斯), ‘sigmoid’等， (default=‘rbf’)

degree: 仅适用于多项式，最高次方(default=3)

gamma: 核函数系数，适用于 ‘rbf’, ‘poly’ and ‘sigmoid’. (default=‘auto’); 1/22

decision_function_shape : 超平面shape, ‘ovo’, ‘ovr’, (default=‘ovr‘),

1. ’ovr’一对多法（one-versus-rest,简称1-v-r SVMs, OVR SVMs）。训练时依次把某个类别的样本归为一类,
   其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数
   值的那类
2. ‘ovo’一对一法（one-versus-one,简称1-v-1 SVMs, OVO SVMs, pairwise）。其做法是在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。

调用库函数计算：建立模型并计算

clf.fit(X_train, y_train ) # 调用库函数计算SVM算法
clf.predict(X_test) # 预测X_test分类结果
clf.support_ # 支持向量的索引，shape=[n_SV,]下标组成的数组
clf.support_vectors_ # 支持向量列表，shape=[n_sv,n_features]
clf.n_support_ # 支持向量所属每个类别个数
clf.decision_function(X_train) # X_train离超平面距离，带方向符号，判断分类依据
clf.score(X_train, y_train) # 计算精度
clf.coef_ # 权重，仅适用于线性核函数
clf.intercept_ # 超平面常数