【机器学习】决策树与随机森林

1.决策树

决策树是一种简单高效并具有强解释性的模型，是基本的分类与回归方法，广泛用于数据分析。

决策树与逻辑回归

决策树的树形模型更接近人的思维方式，对特征一个一个进行处理，可以产生可视化的分类规则，模型具有强解释性。

逻辑回归的线性模型是将所有特征值赋予权重，转换为概率，将大于概率阈值的划分为一类，小于概率阈值的划分为一类。

2 如何构造决策树

决策树的构造思想： 寻找最纯净的划分方法，在数学上叫做纯度，通常可以理解为将不同分类分的足够开。

构造过程：

那么如何选取最优特征值？
ID3算法用的是信息增益，C4.5算法用信息增益率；CART算法使用基尼系数。

2.1 信息增益

2.1.1 信息熵

信息熵是表示随机变量不确定性的变量

信息增益是指知道一个信息Y后能够获取多少关于另外一个相关X的信息（由Y引入而使X的不确定度减小的量）。

存在两个随机事件X,Y ，一个随机事件X具有不确定性H(X)，当X,Y相关联，Y已知时，X的不确定性就会变化，这个变化值就是X的信息熵减去X的条件熵，这就是信息增益。

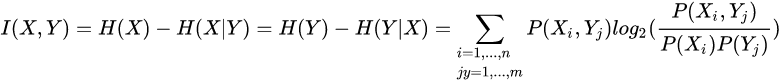
2.1.2 条件熵

条件熵的物理意义是在已知某一信息X前提下，能够获取另外信息Y的信息量，如果两个变量相关联的程度高，那么在知道X的情况下能推断出Y的信息量越多，条件熵就越低（熵是不确定，越确定，熵自然就低）。

2.2 基尼系数

2.3构造决策树

3 剪枝

在构建决策树的时候，我们希望构建的是一颗最矮的决策树，因为最矮，可以有效避免过拟合现象。

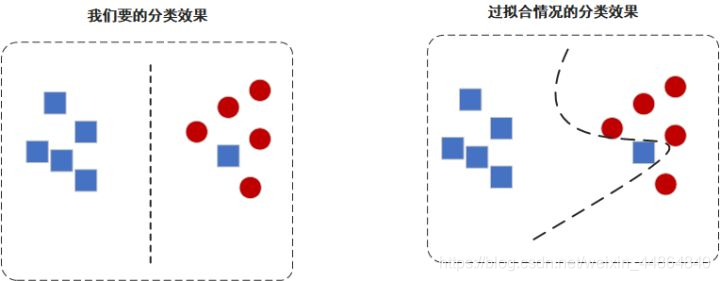
可以看到，一个错误的数据可以很大程度影响最终的分类效果，在构建模型时，我们允许有一定的误差来追求普适性，而不为了追求对训练集的正确性影响分类结果。

剪枝： 从生成的树上裁掉一些子树或叶节点，将其根节点或者父节点作为新的叶子节点。

剪枝分为两种方法：预剪枝和后剪枝
预剪枝：
在构建决策树前，设定一个高度，当构建的决策树达到这个高度，停止建立。

后剪枝：
任由决策树构建完成，构建完成后，从底部开始判断要减掉哪些枝干。

对于预剪枝来讲，它使得决策树的很多分支都没有展开，这不仅降低了过拟合的风险，还显著减少了决策树的训练和预测时间开销。但是另一方面，有些分支的当前划分虽然不能提升泛化性能、甚至可能导致泛化性能暂时下降，但是在其基础上的后续划分却有可能导致性能显著提高，这给预剪枝带来了欠拟合的风险；

对于后剪枝来讲，通常情况下，它比预剪枝决策树保留了更多的分支。后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树，但是其训练时间开销比未剪枝决策树和预剪枝决策树大得多。

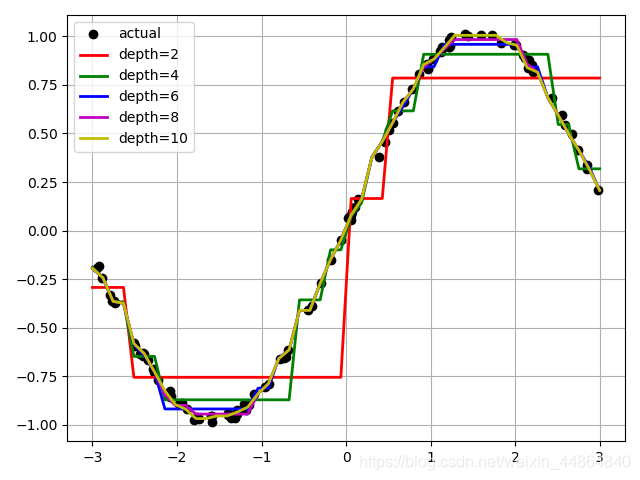
深度对模型的影响

决策树的深度并不是越深越好，这也是在建立模型时需要调参的原因。

import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

N = 100
x = np.random.rand(N) * 6 - 3
x.sort()

y = np.sin(x) + np.random.rand(N) * 0.05
# print(y)

x = x.reshape(-1, 1)
# print(x)

dt_reg = DecisionTreeRegressor(criterion='mse', max_depth=3)
dt_reg.fit(x, y)

x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
y_hat = dt_reg.predict(x_test)

# x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
# y_hat = dt_reg.predict(x_test)

plt.plot(x, y, "y*", label="actual")
plt.plot(x_test, y_hat, "b-", linewidth=2, label="predict")
plt.legend(loc="upper left")
plt.grid()
plt.show()

# 比较不同深度的决策树
depth = [2, 4, 6, 8, 10]
color = 'rgbmy'
dt_reg = DecisionTreeRegressor()
plt.plot(x, y, "ko", label="actual")
x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
for d, c in zip(depth, color):
    dt_reg.set_params(max_depth=d)
    dt_reg.fit(x, y)
    y_hat = dt_reg.predict(x_test)
    plt.plot(x_test, y_hat, '-', color=c, linewidth=2, label="depth=%d" % d)
plt.legend(loc="upper left")
plt.grid(b=True)
plt.show()