定点补码运算器设计：加法器、乘法器与ALU详解-优快云博客

本文详细介绍了定点补码运算器的设计，包括先行进位加法器的逻辑实现，如一位全加器、串行和并行进位加法器的优化，并探讨了补码乘法器的设计原理和Booth算法。此外，还阐述了定点ALU的构造，如判断相等、判断大小和移位操作的逻辑。通过对补码减法算法的解析，展示了如何实现定点运算器的高效计算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

定点补码加法器设计

（1）一位全加器：
1）引脚：
- 三个输入: A, B, Cin
- 两个输出: S, Cout
2）逻辑真值关系：
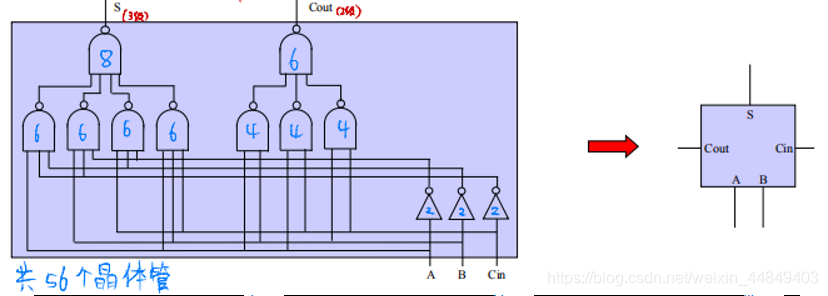
在这里插入图片描述
3）逻辑框图：

（2）串行进位加法器（以16位加法器为例）：
在这里插入图片描述

（3）并行进位逻辑：
1）进位传递：

推导：
$c i + 1 = a i b i + a i * c i + b i * c i = a i * b i + (a i + b i) * c i = g i + p i * c i$
$g i = a i * b i$ （进位生成因子）：只要gi为1, 就有进位；
$p i = a i + b i$ （进位传递因子）：只要pi为1, 就把低位进位向前传递；
四位进位传递举例：
结论：只要低位有一个进位生成, 而且被传递, 则进位输出为1

2）4位并行进位加法器逻辑框图：
在这里插入图片描述
3）改进：以16位加法器为例—分块，块内并行（先行进位），块间串行

4）进一步改进：以16位加法器为例—分块，块内并行，块间并行
① 进位推导：

老办法：产生每块的进位传递因子和进位产生因子
进位传递因子：每一位的传递因子都为1时才能传递
$P = p 0 * p 1 * p 2 * p 3$ （本块可以传递低位进位）
进位产生因子：块内产生进位, 不考虑进位输入
$G = g 3 + (p 3 * g 2) + (p 3 * p 2 * g 1) + (p 3 * p 2 * p 1 * g 0)$ （本块有进位生产）
$c 4 = g 3 + (p 3 * g 2) +$