动态规划解最长公共子串

给定两个字符串str1和str2,输出两个字符串的最长公共子串

题目保证str1和str2的最长公共子串存在且唯一。

示例1

"1AB2345CD","12345EF"

"2345"

备注：

• 1≤∣str1∣,∣str2∣≤5000

动态规划解决

注意这题求的是最长公共子串，不是最长公共子序列，子序列可以是不连续的，但子串一定是连续的。

定义dp[i][j]表示字符串str1中第i个字符和str2种第j个字符为最后一个元素所构成的最长公共子串。如果要求dp[i][j]，也就是str1的第i个字符和str2的第j个字符为最后一个元素所构成的最长公共子串，我们首先需要判断这两个字符是否相等。

如果不相等，那么他们就不能构成公共子串，也就是

dp[i][j]=0;

如果相等，我们还需要计算前面相等字符的个数，其实就是dp[i-1][j-1]，所以dp[i][j]=dp[i-1][j-1]+1;

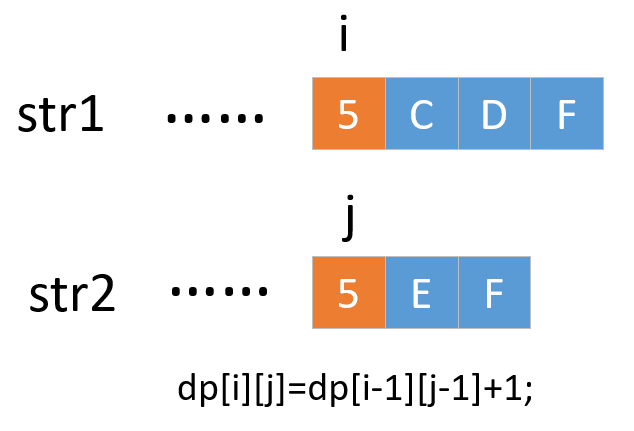
有了递推公式，代码就比较简单了，我们使用两个变量，一个记录最长的公共子串，一个记录最长公共子串的结束位置，最后再对字符串进行截取即可，来看下代码

 public String LCS(String str1, String str2) {
     int maxLenth = 0;//记录最长公共子串的长度
     //记录最长公共子串最后一个元素在字符串str1中的位置
     int maxLastIndex = 0;
     int[][] dp = new int[str1.length() + 1][str2.length() + 1];
     for (int i = 0; i < str1.length(); i++) {
         for (int j = 0; j < str2.length(); j++) {
             //递推公式，两个字符相等的情况
             if (str1.charAt(i) == str2.charAt(j)) {
                dp[i + 1][j + 1] = dp[i][j] + 1;
                //如果遇到了更长的子串，要更新，记录最长子串的长度，
                //以及最长子串最后一个元素的位置
                if (dp[i + 1][j + 1] > maxLenth) {
                    maxLenth = dp[i + 1][j+1];
                    maxLastIndex = i;
                }
            } else {
                //递推公式，两个字符不相等的情况
                dp[i + 1][j+1] = 0;
            }
        }
   }
    //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置
    return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);
}

时间复杂度：O（m*n），m和n分别表示两个字符串的长度

空间复杂度：O（m*n）

代码优化，把二维数组变为一维数组

 public String LCS(String str1, String str2) {
     int maxLenth = 0;//记录最长公共子串的长度
    //记录最长公共子串最后一个元素在字符串str1中的位置
     int maxLastIndex = 0;
     int[] dp = new int[str2.length() + 1];
     for (int i = 0; i < str1.length(); i++) {
         //注意这里是倒叙
         for (int j = str2.length() - 1; j >= 0; j--) {
             //递推公式，两个字符相等的情况
            if (str1.charAt(i) == str2.charAt(j)) {
                dp[j + 1] = dp[j] + 1;
                //如果遇到了更长的子串，要更新，记录最长子串的长度，
                //以及最长子串最后一个元素的位置
                if (dp[j + 1] > maxLenth) {
                    maxLenth = dp[j + 1];
                    maxLastIndex = i;
                }
            } else {
                //递推公式，两个字符不相等的情况
                dp[j + 1] = 0;
            }
        }
    }
    //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置
    return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);
}

时间复杂度：O（m*n），m和n分别表示两个字符串的长度

空间复杂度：O（n），只需要一个一维数组即可