串的定义
串即字符串,是由零个或多个字符组成的有限序列,是数据元素为单个字符的特殊线性表。
串长:串中字符个数(n≥0). n=0 时称为空串 。
空白串 由一个或多个空格符组成的串。
子串:串s中任意个连续的字符序列叫s的子串; S叫主串
子串位置 子串的第一个字符的序号
字符位置:字符在串中的序号。
串相等 串长度相等,且对应位置上字符相等。
串的抽象数据类型定义
ADT Sting{
Objects: D={ai | ai∈CharacterSet, i=1, 2,…,n, n≥0}
Relations: R1={<ai-1,ai> | ai-1,ai ∈D, i=2, …,n}
functions: // 有13种之多
StrAssign(&T, chars) // 串赋值,生成值为chars的串T
StrCompare(S,T) // 串比较,若S>T,返回值大于0…
StrLength(S) // 求串长,即返回S的元素个数
Concat(&T, S1, S2) // 串连接,用T返回S1+S2的新串
SubString(&Sub, S, pos, len) // 求S中pos起长度为len的子串
……
Index(S, T, pos) // 返回子串T在pos之后的位置
Replace(&S, T,V) // 用子串V替换子串T
}ADT Sting
串的表示和实现
首先强调:串与线性表的运算有所不同,是以“串的整体”作为操作对象,例如查找某子串,在主串某位置上插入一个子串

定长顺序存储特点:用一组连续的存储单元来存放串,直接使用定长的字符数组来定义,数组的上界预先给出,故称为静态存储分配。
例如
#define Maxstrlen 255 //用户可用的最大串长
typedef struct{
char SString[ Maxstrlen+1 ]; // 下标0的分量闲置不用
int length;
} SString s; //s是一个可容纳255个字符的顺序串。
C语言约定在串尾加结束符 ‘ \0’,以利操作加速,但不计入串长;
若字符串超过Maxstrlen 则自动截断(因为静态数组存不进去)
串的连接
串连接Concat(&T, S1, S2)
Status Concat( sstring &T, sstring S1, sstring S2)
{ if ( S1[0] +S2[0] <= MAXSTRLEN) // 未截断
{ T[1..S1[0]] = S1[ 1..S1[0]];
T[ S1[0]+1 .. S1[0]+S2[0] ] = S2[ 1 .. S2[0] ];
T[0] = S1[0] + S2[0]; uncut = TRUE;
}
else if ( S1[0] < MAXSTRSIZE ) // 截断
{ T[ 1..S1[0] ] = S1[ 1..S1[0] ];
T[ S1[0] +1 .. MAXSTRLEN ] = S2[ 1.. MAXSTRLEN- S1[0]];
T[0] = MAXSTRLEN; uncut = FALSE;
}
else { T[ 0.. MAXSTRLEN ] = S1[ 0.. MAXSTRLEN ]; // 截取(仅取S1)
uncut = FALSE;
}
return uncut;
} // Concat
想存放超长字符串怎么办?——静态数组有缺陷
改用动态分配的一维数组 堆
堆分配存储特点:仍用一组连续的存储单元来存放串,但存储空间是在程序执行过程中动态按需分配而得
Typedef struct {
char *ch; // 若非空串,按串长分配空间; 否则 ch = NULL
int length; //串长度
}HString
链式存储特点 :用链表存储串值,易插入和删除
块链类型定义
#define CHUNKSIZE 80 //可由用户定义的块大小
typedef struct Chunk { //首先定义结点类型
char ch [ CHUNKSIZE ]; //结点中的数据域
struct Chunk * next ; //结点中的指针域
}Chunk;
typedef struct { //其次定义用链式存储的串类型
Chunk *head; //头指针
Chunk *tail; //尾指针
int curLen; //结点个数
} Lstring; //串类型只用一次,前面可以不加Lstring
串与线性表的运算有所不同,是以“串的整体”作为操作对象,例如查找某子串,在主串某位置上插入一个子串等。
这类操作中均涉及到定位问题,称为串的模式匹配。它是串处理系统中最重要的操作之一。
串的模式匹配算法
模式匹配(Pattern Matching) 即子串定位运算(Index函数)算法目的:确定主串中所含子串第一次出现的位置(定位)
——即如何实现 Index(S,T,pos)函数
初始条件:串S和T存在,T是非空串,1≤pos≤StrLength(s)
操作结果:若主串S中存在和串T值相同的子串,则返回它在主串S中第pos个字符之后第一次出现的位置;否则函数值为0。
注:S称为被匹配的串,T称为模式串。若S包含串T,则称
“匹配成功”,否则称 “匹配不成功”
BF算法 (又称古典或经典的、朴素的、穷举的)
KMP算法(特点:速度快)
BF算法设计思想:
将主串的第pos个字符和模式的第1个字符比较,
若相等,继续逐个比较后续字符;
若不等,从主串的下一字符(pos+1)起,重新与第一个字符比较。
直到主串的一个连续子串字符序列与模式相等 。返回值为S中与T匹配的子序列第一个字符的序号,即匹配成功。
否则,匹配失败,返回值 0 .
Int Index(SString S, SString T, int pos) {
i=pos; j=1;
while ( i<=S.length && j<=T.length ) {
if (S.ch[i] = = T.ch[j] ) {++i; ++j} //继续比较后续字符
else {i=i-j+2; j=1;} //指针回溯到 下一首位,重新开始匹配
}
if(j>T.length) return i-T.length; //子串结束,说明匹配成功
else return0;
}//Index
若n为主串长度,m为子串长度,则串的BF匹配算法最坏的情况下需要比较字符的总次数为
(n-m+1)m=O(nm)
最恶劣情况是:主串中前面n-m个位置都部分匹配到子串的最后一位时出现不等,此时需要将指针i回溯,并从模式的第一个字符开始重新比较,整个匹配过程中,指针i需回溯(n-m)次,则while循环次数为(n-m+1)*m。
但一般情况下BF算法的时间复杂度为O(n+m)
**
KMP算法
**
能否利用已经部分匹配的结果而加快模式串的滑动速度?
能!而且主串S的指针i不必回溯!可提速到O(n+m)!
需要讨论两个问题:
① 如何“记忆”部分匹配结果?
② 如何由“记忆”结果计算出主串S第i个字符应该与模式T中哪个字符再比较?即确定模式T中的新比较起点k.
抓住部分匹配结果的两个特征:
设目前应与T的第k字符开始比较
则T的k-1~1位=S前i-1~i-(k-1)位
刚才肯定是在S的i处和T的第j字符 处失配
则S前i-1~i-(k-1)位=T的j-1~j-(k-1)位
两式联立可得:‘T1…Tk-1’=‘Tj-(k-1) …Tj-1’
注意:j 为当前已知的失配位置,我们的目标是计算新起点 k,
仅剩一个未知数k,理论上已可解,且k仅与模式串T有关!
根据模式串T的规律: ‘T1…Tk-1’=‘Tj-(k-1) …Tj-1’
和已知的当前失配位置j ,可以归纳出计算新起点 k的表达式。
令k = next[ j ],则
讨论:
① next[ j ]有何意义?
一旦失配,应从模式串T中第next[ j ]个字符开始与S的失配点i 重新匹配!
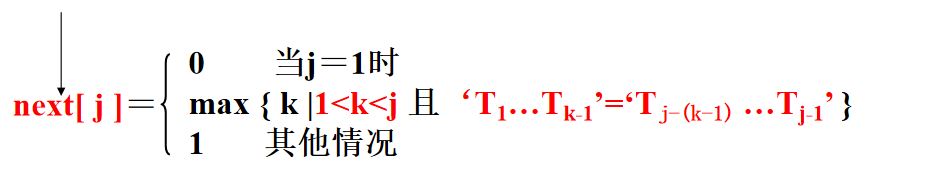

MP算法的实现—即Index( )操作的实现
第一步,先把模式T所有可能的失配点j所对应的next[j]计算出来;
第二步:执行定位函数index_kmp (与BF算法模块非常相似)
Int Index_KMP(SString S, SString T, int pos) {
i=pos; j=1;
while ( i<=S[0] && j<=T[0] ) {
if (j==0|| S[i] = = T[j] ) {++i, ++j} //不失配则继续比较后续字符
else {j=next[j];} //S的i指针不回溯,从T的k位置开始匹配
}
if(j>T[0]) return i-T[0]; //子串结束,说明匹配成功
else return0;
}//Index_KMP
求解next[j] 算法
void get_next (SString T, int &next[ ] )
{ //next函数值存入数组next
i=1; next[1]=0; j=0;
while(i<T[0] )
{
if ( j= = 0||T[i]= = T[j] )
{ ++i; ++j; next[i]=j; }
else j=next[j];
} // while
}// get_next
next [ j ]是否完美无缺?
答:未必,例如当 S=‘a b a a a a b’,T=‘a a a a b’时 ,仍有
多余动作
这时可引入修正的next数组,这里略
数组
数组和广义表的特点:一种特殊的线性表
元素的值并非原子类型,可以再分解,表中元素也是一个线性表(即广义的线性表)。
所有数据元素仍属同一数据类型
数组: 由一组名字相同、下标不同的变量构成
注意: 本章所讨论的数组与高级语言中的数组有所区别:
高级语言中的数组是顺序结构;而本章的数组既可以是顺序的,也可以是链式结构,用户可根据需要选择。
讨论:“数组的处理比其它复杂的结构要简单”,对吗
答:对的。因为:
① 数组中各元素具有统一的类型;
② 数组元素的下标一般具有固定的上界和下界,即数组一旦被定义,它的维数和维界就不再改变。
③数组的基本操作比较简单,除了结构的初始化和销毁之外,只有存取元素和修改元素值的操作。
数组的顺序存储
问题:计算机的存储结构是一维的,而数组一般是多维的,怎样存放?
解决办法:事先约定按某种次序将数组元素排成一列序列,
然后将这个线性序列存入存储器中。
例如:在二维数组中,我们既可以规定按行存储,也可以规定按列存储。
注意:
若规定好了次序,则数组中任意一个元素的存放地址便有规律可寻,可形成地址计算公式;
约定的次序不同,则计算元素地址的公式也有所不同;
C和PASCAL中一般采用行优先顺序;FORTRAN采用列优先。
无论规定行优先或列优先,只要知道以下三要素便可随时求出任一元素的地址(这样数组中的任一元素便可以随机存取!)
*二维数组行优先存储时的地址公式为:LOC(aij)=LOC(ac1,c2) + [(i-c1)*(d2-c2+1)+j-c2)]L
*二维数组列优先存储的通式为:
LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c1)]L
讨论:
- 什么是压缩存储?
若多个数据元素的值都相同,则只分配一个元素值的存储空间,且零元素不占存储空间。 - 什么样的矩阵具备压缩条件?
特殊矩阵(对称矩阵,对角矩阵,三角矩阵)
和稀疏矩阵。 - 什么叫稀疏矩阵?
矩阵中非零元素的个数较少(一般小于5%)
广义表
广义表是线性表的推广,也称为列表(lists)
记为: LS = ( a1 , a2 , ……, an )
在广义表中约定:
① 第一个元素是表头,而其余元素组成的表称为表尾;
② 用小写字母表示原子类型,用大写字母表示列表。
讨论:广义表与线性表的区别和联系?
广义表中元素既可以是原子类型,也可以是列表;
当每个元素都为原子且类型相同时,就是线性表。
有次序性
有长度
有深度
可递归
可共享
特别提示:任何一个非空表,表头可能是原子,也可能是列表;但表尾一定是列表。
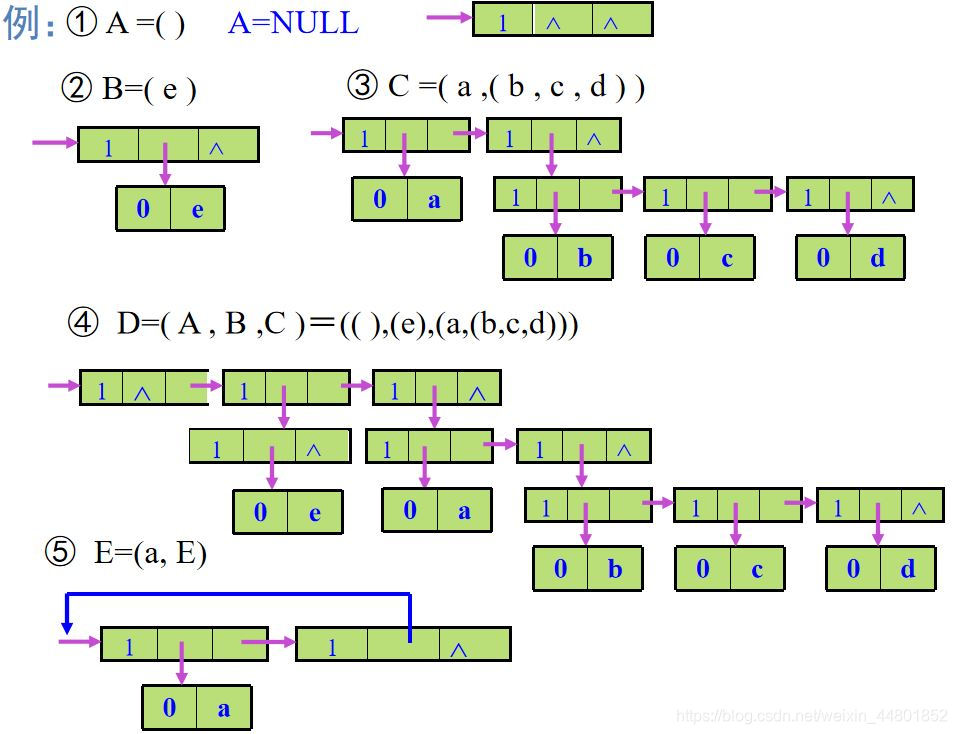
求下列广义表的表长
1)A =( )
2)B = ( e )
3)C =( a ,( b , c , d ) )
4)D=( A , B ,C )
5)E=(a, E)
n=0,因为A是空表
n=1,表中元素e是原子
n=2,a 为原子,(b,c,d)为子表
n=3,3个元素都是子表
n=2,a 为原子,E为子表
GetHead( L) ——取表头(可能是原子或列表);
GetTail(L ) ——取表尾(一定是列表)
- GetTail【(b, k, p, h)】= (k,p,h) ;
- GetHead【( (a,b), (c,d) )】= (a,b) ;
- GetTail【( (a,b), (c,d) )】= ((c,d)) ;
- GetTail【 GetHead【((a,b),(c,d))】】= (b) ;
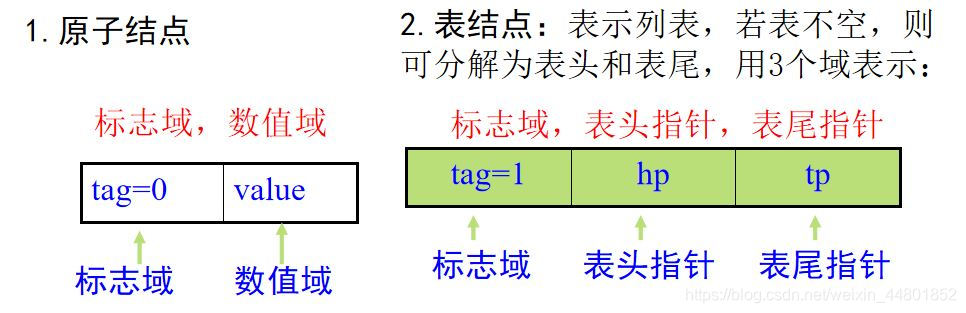
广义表的存储结构
由于广义表的元素可以是不同结构(原子或列表),难以用顺序存储结构表示 ,通常用链式结构,每个元素用一个结点表示。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








