C语言模拟栈和队列（重点讨论队列判空的问题）

于 2019-10-19 16:04:04 发布
阅读量572 收藏 7
点赞数 1
分类专栏： 数据结构(Data Structure) 文章标签： 数据结构 栈和队列 队列判空方法 C语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_44788162/article/details/102559255
版权
栈和队列
1. 栈
1.1 栈的概念及结构

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。栈中的数据元素遵守后进先出的原则。
压栈：将数据压入栈顶。
出栈：将栈顶元素弹出。

1.2 栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。
栈的结构体定义如下：

typedef int STDataType;

typedef struct Stack
{
	STDataType* s;
	int top; // 栈顶
	int capacity; // 容量
}Stack;

栈的相关操作：

//初始化
void StackInit(Stack* ps) {
	assert(ps);
	ps->s = (STDataType *)malloc(sizeof(STDataType));
	ps->top = -1;
	ps->capacity = 1;
}

//栈的大小
int StackSize(Stack* ps) {
	assert(ps);
	return ps->capacity;
}

//销毁栈
void StackDestory(Stack* ps) {
	assert(ps);
	free(ps->s);
	ps->capacity = 0;
	ps->top = -1;
}

//入栈
void StackPush(Stack* ps, STDataType x) {
	assert(ps);
	if (++ps->top == StackSize(ps)) {
		ps->capacity = ps->capacity * 2;
		ps->s = (STDataType *)realloc(ps->s, sizeof(STDataType) * ps->capacity);
	}
	ps->s[ps->top] = x;
}

//判断栈空
int StackIsEmpty(Stack* ps) {
	assert(ps);
	if (ps->top == -1) {
		return 1;
	}
	return 0;
}

//出栈
void StackPop(Stack* ps) {
	if (StackIsEmpty(ps)) {
		printf("出栈失败! 栈已空.\n");
		return;
	}
	--ps->top;
}

//提取栈顶元素
STDataType StackTop(Stack* ps) {
	assert(!StackIsEmpty(ps));
	return ps->s[ps->top];
}
2. 队列
2.1 队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出的特点。
队尾：进行入队操作的一端。
队头：进行出队操作的一端

2.2 队列的实现

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队时将要把数组的每个元素都移动一遍，效率会比较低。
队列的结构体定义如下，这里使用指针指向队头队尾：

typedef int QUDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QUDataType data;
}QueueNode;

typedef struct Queue
{
	QueueNode* front; // 队头
	QueueNode* rear; // 队尾
}Queue;

而使用链表时会有判断队列是否为空的问题，根据队列的定义，队头队尾指针应分别指向队头和队尾元素，而插入第一个元素之后，队头和队尾都指向了同一个元素，因此不能使用队头等于队尾来判断队列是否为空，而应使用其他方法来判断，如图：
在这里插入图片描述
以下分三种情况进行讨论：

（1）第一次入队操作时将队尾指针指向NULL；
（2）第一次入队操作时将队头指针指向NULL；
（3）初始化的时候增加一个空节点，队尾指针在每次入队后指向一个空节点。

对于（1）、（2），入队一个节点后：
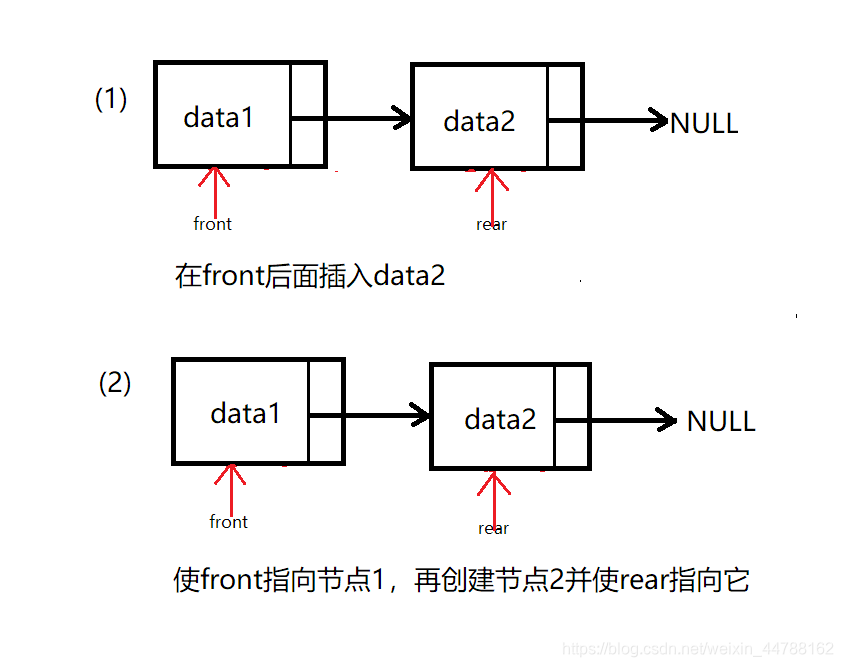
在这里插入图片描述
入队第二个节点：
在这里插入图片描述
出队情况：
对于（1），在队头追上队尾并且队尾不为NULL时，将队尾置为NULL，最后还可以将队头元素出队一次；
对于（2），在队头追上队尾时，将队头置为NULL，最后还可以将队尾元素出队一次。
因此，（1）、（2）的判空方法为：判断队头队尾是否同时为NULL

对于（3），在初始化队列结构的同时创建一个空节点（没有保存数据），并使头尾指针指向这个节点：
图1
入队一个元素：
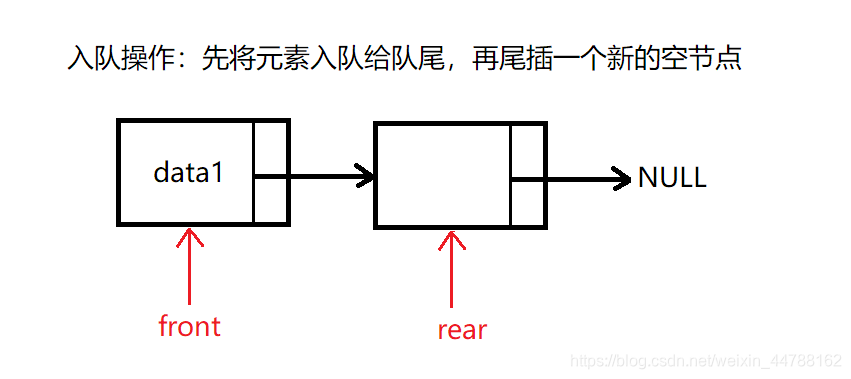
在这里插入图片描述
出队也是将队头元素出队，并移动队头指针，若队头追上队尾，则它们又指向了同一个空的节点空间，此时队列也为空。这样，不仅操作起来简单，逻辑上也和队列数据结构的定义一致。
也就是说，无论是从逻辑结构还是操作复杂度上来看，方案（3）才是比较好的方法，只是会有一个节点的空间浪费了而已。

（3）这么好的方法当然是要自己动手实现嘛，代码我就不贴了，我贴一贴（1）这种憨憨操作的代码，大家看一看这种方法写起来有麻烦。

//初始化
void QueueInit(Queue* pq) {
	assert(pq);
	pq->front = NULL;
	pq->rear = NULL;
}

//判断队列是否为空
int QueueEmpty(Queue* pq) {
	assert(pq);
	return pq->front == NULL;
}

//销毁队列
void QueueDestory(Queue* pq) {
	assert(pq);
	QueueNode *next;
	while (!QueueEmpty(pq)) {
		next = pq->front->next;
		free(pq->front);
		pq->front = next;
	}
	free(pq->rear);
	pq->front = NULL;
	pq->rear = NULL;
}

//求队长
int QueueSize(Queue* pq) {
	assert(pq);
	QueueNode *cur = pq->front;
	int count = 0;
	while (cur) {
		++count;
		cur = cur->next;
	}
	return count;
}

//生成新节点
QueueNode* BuyQueueNode(QUDataType x) {
	QueueNode *node;
	node = (QueueNode *)malloc(sizeof(QueueNode));
	node->data = x;
	node->next = NULL;
	return node;
}

//入队
void QueuePush(Queue* pq, QUDataType x) {
	assert(pq);
	QueueNode *node = BuyQueueNode(x);
	if (pq->front == NULL) {
		pq->front = pq->rear = node;
		pq->front->next = pq->rear->next = NULL;
	}
	else {
		pq->rear->next = node;
		pq->rear = node;
		node->next = NULL;
	}
}

//出队
void QueuePop(Queue* pq) {
	assert(pq);
	if (QueueEmpty(pq)) {
		printf("出队失败! 队列已空.\n");
		return;
	}
	QueueNode *cur = pq->front;
	if (pq->front == pq->rear && pq->rear) {
		pq->rear = pq->rear->next;
	}
	pq->front = pq->front->next;
	free(cur);
}

//取队头元素
QUDataType QueueFront(Queue* pq) {
	assert(pq);
	if (QueueEmpty(pq)) {
		printf("队中无元素!\n");
		return -1;
	}
	return pq->front->data;
}

//取队尾元素
QUDataType QueueBack(Queue* pq) {
	assert(pq && !QueueEmpty(pq));
	if (pq->rear == NULL) {
		return pq->front->data;
	}
	return pq->rear->data;
}

以上各函数中，求队列长度的函数QueueSize是不常用的，当然也可以用这个函数来判空，这样就完美解决了我之前讨论的队中只有一个元素的问题，但是效率非常低，所以不推荐使用（反正我是没有用）。

2.3 循环队列

循环队列是一种特殊的队列，循环队列在逻辑结构上是一个环，它的长度是固定的，无法扩容。优点是解决了使用数组实现队列时出队的时间复杂度问题，缺点是不好判断队列是否已满。
循环队列常应用于解决排队论问题：队列的大小可以视作服务台的个数或服务系统一次最多能服务的顾客的人数，当队列已满时，拒绝入队，队列外的顾客就需要等其他的顾客被服务完后才能入队。关于排队论的详细讨论请参考《运筹学》。
判断队列是否满的方法一般有两种：
（1）比较常用的方法是，判断队尾加一是否追上队头，这样与2.2中的方案（3）一样，会造成一个单位的空间的浪费，但是极大方便相关操作的编写。如果使用这种方法，队尾始终指向队列中最后一个元素的下一个空间，如图所示，也就是说，队尾指向的空间就这样被浪费了。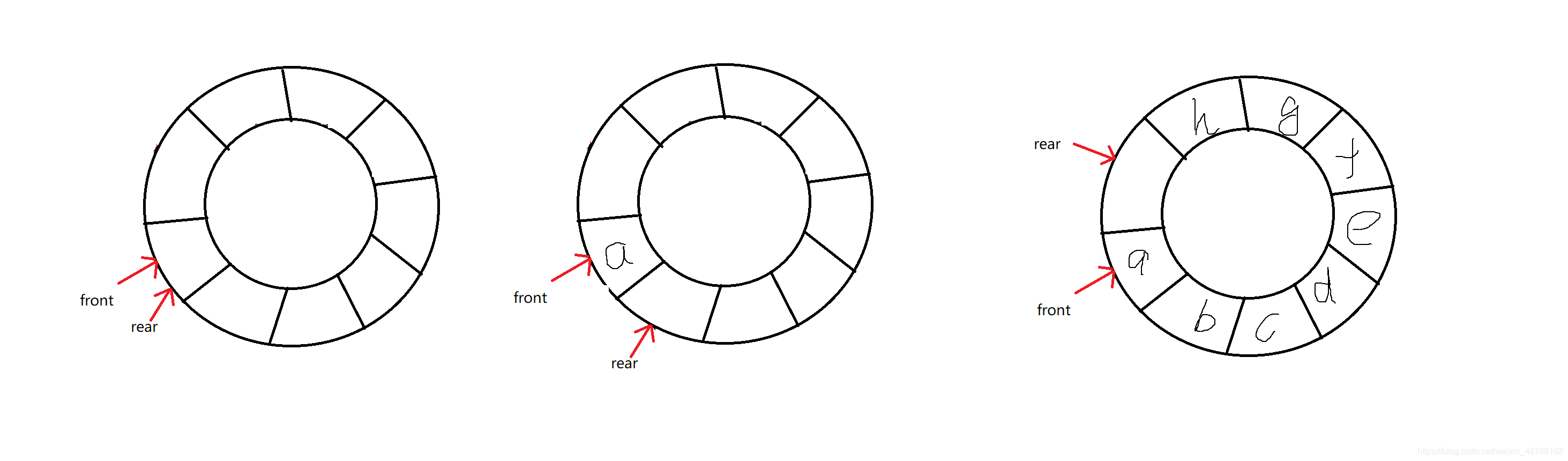在这里插入图片描述
（2）第二种方法是设置一个bool变量，即0-1变量，使用这个变量的状态来判断队头队尾重叠时队列的状态。
举个例子：设一个bool变量FO_E，FO_E为 0 时队空(empty)，FO_E为 1 时队满(full)，这样，我们置这个变量的初值为0，当我们进行入队操作时置为1，出队时置0。当队头队尾重叠时检测FO_E的状态即可判断队列是空还是满。
循环队列的结构体定义如下：

typedef int CQDataType;

typedef struct CircleQueue
{
	CQDataType *cq_arr;
	int front;
	int rear;
	int cq_size;
}CircleQueue;

使用方法（1）来判断队列状态，相关操作代码如下：

//初始化循环队列
void InitCQueue(CircleQueue* cq, int length) {
	assert(cq);
	cq->front = 0;
	cq->rear = 0;
	cq->cq_arr = (CQDataType *)malloc(sizeof(CQDataType) * length);
	cq->cq_size = length;
}

//销毁队列
void CQueueDestory(CircleQueue* cq) {
	assert(cq);
	free(cq->cq_arr);
	cq->front = cq->rear = 0;
}

//判断队列是否为空
int IsEmptyCQueue(CircleQueue* cq) {
	assert(cq);
	return cq->front == cq->rear;
}

//判断队满
int IsFullCQueue(CircleQueue *cq) {
	assert(cq);
	return (cq->rear + 1) % cq->cq_size == cq->front;
}

//入队
void CQueuePush(CircleQueue* cq, CQDataType x) {
	if (IsFullCQueue(cq)) {
		printf("入队失败, 队列已满!\n");
		return;
	}
	cq->cq_arr[cq->rear] = x;
	cq->rear = (cq->rear + 1) % cq->cq_size;
}

//出队
void CQueuePop(CircleQueue* cq) {
	if (IsEmptyCQueue(cq)) {
		printf("队列为空!\n");
		return;
	}
	cq->front = (cq->front + 1) % cq->cq_size;
}

//提取队头元素
CQDataType CQueueFront(CircleQueue* cq) {
	if (IsEmptyCQueue(cq)) {
		printf("获取队头失败, 队列已空!\n");
		return -1;
	}
	return cq->cq_arr[cq->front];
}

虽然循环队列在逻辑结构上定义为一个环，但是计算机并没有这样的功能给你创建一个环形数组出来，因此需要我们手动实现这个环：当队尾(队头)超出了队列的实际大小时，取它与队列大小的余数。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值