传送门
一开始没有考虑奇环和偶环相交的情况,后来被大神的操作点醒,就ac了,感觉数据挺水的。
首先介绍一下,二分图的条件:点的数量必须大于2。无自环。若存在环,则该环边数必为偶数。
题意是让我们删去一条边,使得该图剩下为二分图,那么应该删去的边必须满足
1:若某个奇环和偶环有重边,那么不可以删重边,只可以删奇环上的边。
2:删去此边,图中再无自环,也无奇环。
我们需要找到环中所有的边,这里可以使用前缀和num数组来存边,num是存有多少个环用了此边,奇环用了num+1,偶环用了num-1。
Num存图中奇环总数量
例如下图:
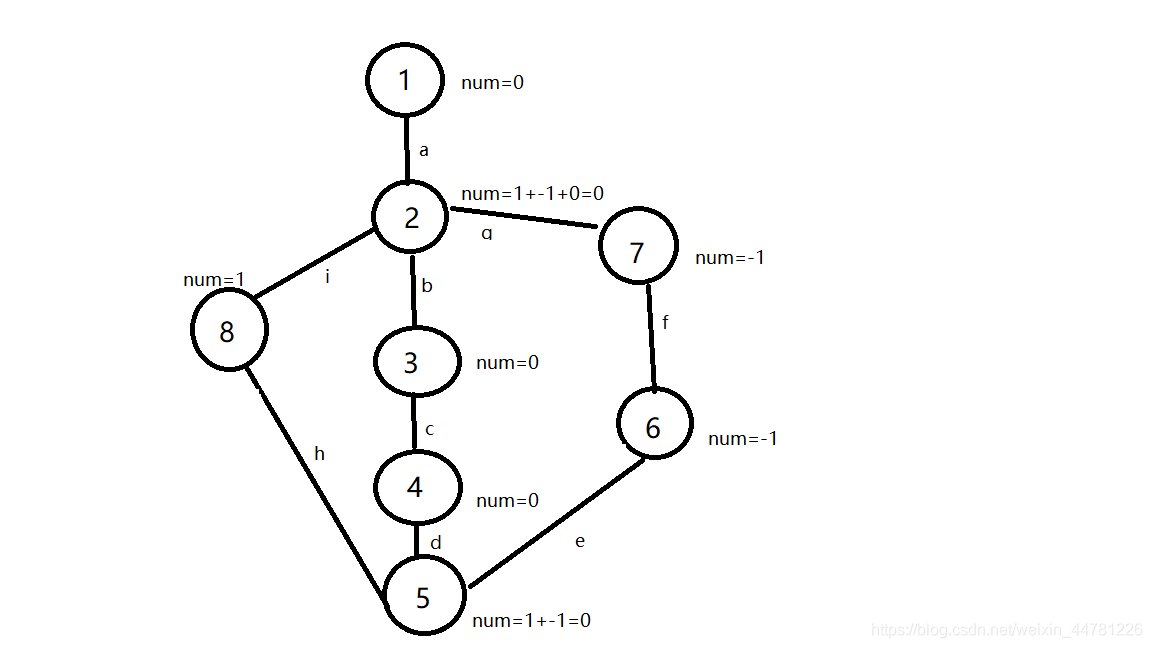
我们由图,易知,ibcdh为奇环,gfedcb为偶环,重边是bcd,所以我们必须删ih,否则存在外围gfehi为奇环。
当我们递归1-2-3-4-5-8-1时,遇到了一个奇环,那么num[8]++,num[2]–,Num++,并且把i这一条边用untree存起来;
当我们再递归5-6-7-1时,遇到了一个偶环,那么num[7]–,num[2]++;
运行完之后就变成上面模样。
我们怎么找符合条件的边,若删除此边,必须使所有的奇边均消失,那么就是此边连的点的num值为Num即可,也就是图中的num[8]=1=Num,而节点8所连的就是h边,又因为图中只有一个奇环,因此又必须加上untree=i这条边。
至于可以删的边,也是要分情况的。
1:有奇环
(1)有自环:return
(2)无自环:奇环上所有边均可(注意,如果只有一个奇环,那么要把untre加上,否则不需要)
2:无奇环
(1) 有自环:自环数量>1,return。等于1,就是自环这一条边
(2) 无自环:任意边均可。
#include<bits/stdc++.h>
using namespace std;
const int MX=2e6+9;
struct node{
int to;
int id;
int next;
}edge[MX];
int tot=0,head[MX];
void add(int u,int v,int id){
edge[tot].to=v;
edge[tot].id=id;
edge[tot].next=head[u];
head[u]=tot++;
}
int num[MX],cnt,dis[MX],pos[MX];
int Self,Num,untree;
void dfs(int u,int fa){
pos[u]=1;
for( int i=head[u] ; ~i ; i=edge[i].next ){
if( i==fa )
continue;
int to=edge[i].to;
if( !pos[to] ){
dis[to]=dis[u]+1; // 没走过就继续递归
dfs(to,i^1); // 这里说明一下为什么是i^1,因为是无向图,所以每条边其实是用双向边表示,
// 比如1到2,2到1两条边。如果用了1到2这条边,那么下一次递归到点2,2就不可以使用2到1这条边
// 而1到2,2到1这两条边,在链式星的编号中,差别为1.
num[u]+=num[to];
}
else{ // 走过就说明碰见环了
if( dis[to]>dis[u] ) // 为什么会有这一步呢?比如2-3-4-5-6-7-(2)-(5)-8-(2)递归完,要回到节点2,现在2不可以走3,只可以走8或7,但是已经走过了(因为是无向边),就出现了这种情况。
continue;
int L=dis[u]-dis[to]+1;
if( L&1 ){ // 若是奇环,奇环所有边+1,并且存好非树边
Num++;
num[to]--;
num[u]++;
untree=edge[i].id;
}
else{ // 若是偶环,则要把偶环所有边-1,
num[u]--;
num[to]++;
}
}
}
}
vector<int> ans,self;
void dfs1(int u,int fa){
if( num[u]==Num )
ans.push_back(edge[fa].id);
pos[u]=1;
for( int i=head[u] ; ~i ; i=edge[i].next ){
int to=edge[i].to;
if( !pos[to] )
dfs1(to,i^1);
}
}
int main()
{
freopen("input.txt","r",stdin);
memset(head,-1,sizeof(head));
int n,m;
scanf("%d %d",&n,&m);
for( int i=1 ; i<=m ; i++ ){
int u,v;
scanf("%d %d",&u,&v);
if( u==v ){ // 自环都存起来
Self++;
self.push_back(i);
}
else{
add(u,v,i);
add(v,u,i);
}
}
if( n<2 || Self>1 ){ //如果有自循环超过2个,或者n小于2直接return
printf("0\n");
return 0;
}
memset(pos,0,sizeof(pos));
for( int i=1 ; i<=n ; i++ ) // 把所有的点都遍历一遍
if( !pos[i] )
dfs(i,-1);
if( Num ){ // 有奇环
if( Self==1 ) // 有自环
printf("0\n");
else{
memset(pos,0,sizeof(pos));
for( int i=1 ; i<=n ; i++ )
if( !pos[i] )
dfs1(i,-1);
if( Num==1 ) // 若只有一个奇环,无自环,便要加上那个非树边
ans.push_back(untree);
sort(ans.begin(),ans.end());
printf("%d\n",ans.size());
for( int i=0 ; i<ans.size() ; i++ )
printf("%d%c",ans[i],i==ans.size()-1?'\n':' ');
}
}
else{ // 无奇环
if( Self==1 ) // 有自环
printf("1\n%d\n",self[0]);
else{ // 无自环
printf("%d\n",m);
for( int i=1 ; i<=m ; i++ )
printf("%d%c",i,i==m?'\n':' ');
}
}
return 0;
}
























 9144
9144

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








