动态规划经典算法之博弈问题

开篇

最近有点懒，这种长文好久没更新了。今天聊一个比较有趣的智力问题——博弈问题。
我们一定遇到过这种问题，两个地主分宝石或者是两个人抢硬币，问你怎么做能赢得更多的奖励巴拉巴拉巴拉。这种问题其实归根到底，都是博弈问题。只不过是换了种形式。下次再有人问你类似的问题时，你就可以告诉他:“我懒得思考这么简单的问题，我给你个算法好了”。是不是很牛逼。话不多说，我们开始吧。

问题描述

两个人面前有一排石头堆，有一个数组piles表示，piles[i]表示第i堆石子有多少个。你们轮流拿石头，一次拿一堆，但是只能拿走最左边或者最右边的石头堆。所有石头被拿完后，谁拥有的石头多谁就获胜。
石头堆数可以是任意正整数，石头的总数也可以是任意正整数，这样就能打破先手必胜的就局面了。比如有三堆石头piles = [1,100,3],先手不管拿1还是3，能够决定胜负的100都会被后手拿走，这样的一定后手胜。
我们要设计一个算法，返回先手和后手的最后得分(石头总数)之差，比如上述例子中先手得到4分，而后手得到了100分，所以两者的差为-96分。

算法分析

其实讲真，这道题算是一个hard难度的问题，它的难点主要是两个人要轮流进行选择，我们应该如何变成表示这个选择过程呢？
受到前几篇文章思路的启发，我们应该已经明确了动态规划问题的解法了——明确dp数组的含义，然后只要找到状态和选择，一切就完成了。
一.定义dp数组的含义
介绍dp数组的含义之前，大家不妨看一下dp数组最后的样子

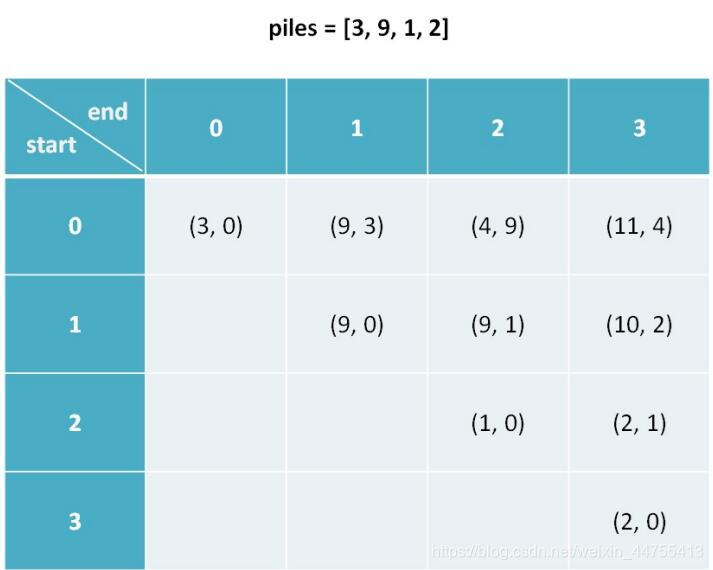
这里面的每一个数值都是一个元组，元组的第一个元素是first，即当前先手得分，第二个元素是second，即后手得分。我们都简写为fir,sec.

dp[i][j].fir表示，对于piles[i...j]这部分石头堆，先手能获得的最高分数
dp[i][j].sec表示，对于piles[i...j]这部分石头堆，后手能获得的最高分数

我们想求的答案就是先手和后手的最终分数之差，按照这个定义就是dp[0][n-1].fir与dp[0][n-1].sec，即面对整个piles，先手的最优得分和后手的最优得分之差。
二.状态转移方程
写状态转移方程很简单，首先要找到所有的状态和每个状态可以做的选择，然后择优。
这个选择不是从状态列表中选择，而是穷举可以解决问题的方式。
根据dp数组的定义，状态有以下三个1.piles开始的位置 2.piles结束的位置 3.当前轮到的人找到了这三个状态就算你暴力依次穷举应该都可以解决问题，但这是时间复杂度的问题。

dp[i][j][fir or sec]
0 <= i < piles.length()
0 <= j < piles.length()

对于这个问题的每个状态，可以作的选择有两个：选择最左边的那堆石头或者选择最右边的那堆石头。我们可以穷举所有状态：

n = piles.length
for 0 <= i < n:
	for j<=i<n:
		for who in {fir,sec}:
			dp[i][j][who] = max(left,right)

这就是我们的穷举大体框架，下面我们来完成最重要的部分：写出状态转移方程

dp[i][j].fir = max(piles[i] + dp[i+1][j].sec,piles[j]+dp[i][j-1].sec)
dp[i][j].fir = max(选择最左边的石头堆，选择最右边的石头堆)
#解释一下：我现在是先手，面对piles[i...j]，我有两种选择：
#要么选择最左边的石头，然后面对piles[i+1....j]
#要么选择最右边的石头,然后面对piles[i....j-1]
#无论做哪种选择，做完选择之后轮到了对方，我变成了后手。
if 先手选择左边:
	dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
	dp[i][j].sec = dp[i][j-1].fir
#解释：我作为后手，要等先手做完选择才可以做选择，有两种情况：
#如果先手选择了最左边那一堆，给我留下了piles[i+1....j]
#此时轮到了我，我变成了先手
#如果先手选择了最右边那一堆，给我留下了piles[i....j-1]
#此时轮到了我，我变成了先手

状态转移方程有了，我们再说一下base case:

当0<=i==j<n时:
dp[i][j].fir = piles[i]
dp[i][j].sec = 0
#解释：i和j相等就是说面前只有一堆石头piles[i]
#那么先手得分就是piles[i]
#后手得分就是0

可以发现base case是写着斜着的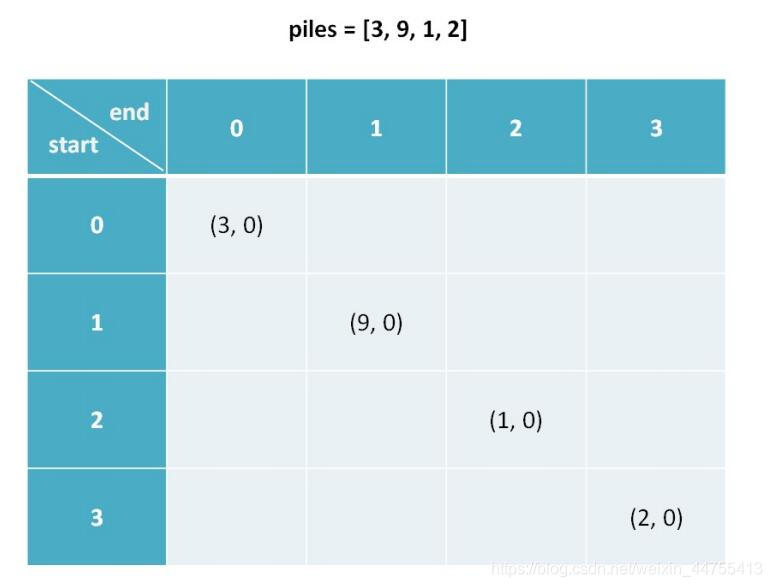

我们在推算dp[i][j]时其实只用到了dp[i+1][j]和dp[i][j-1]，所以dp table应该是这样的：

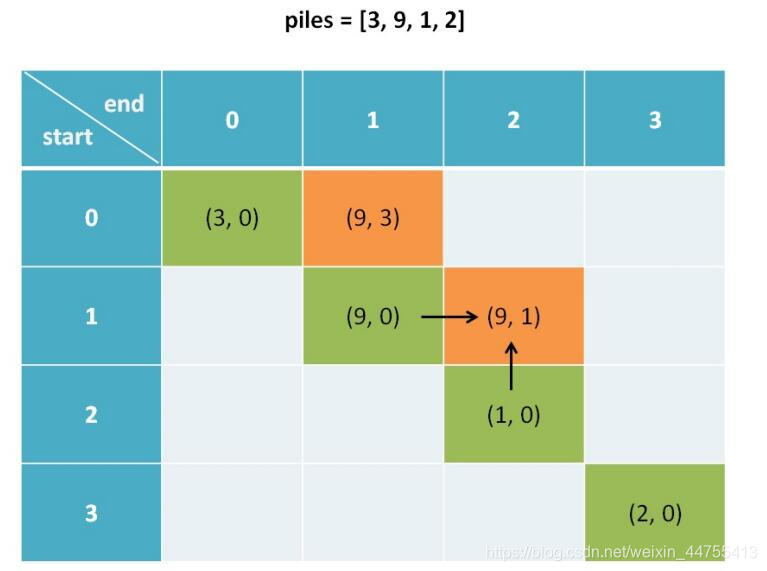
所以我们可以发现，我们不能一行一行的遍历，因为有很多值都是未知的，我们只能斜着遍历。
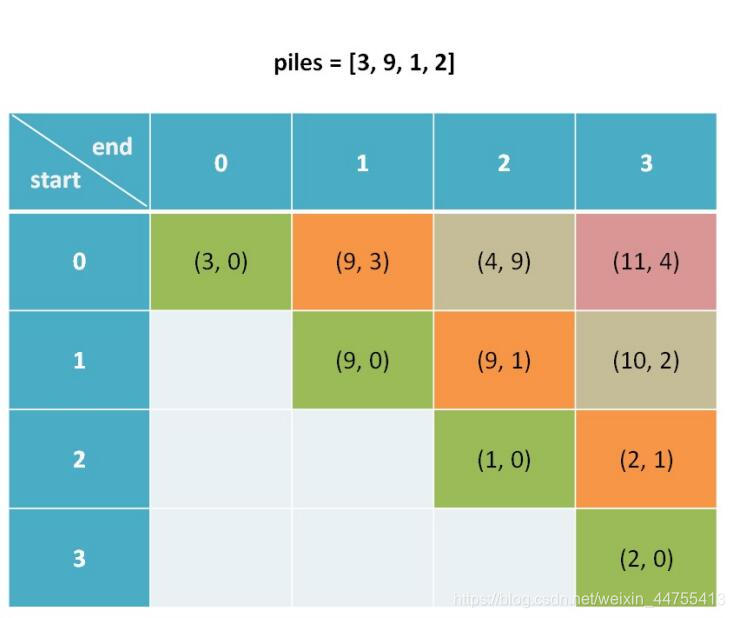千万别告诉我你们不会怎么用代码实现斜着遍历！好吧，其实一开始我也不会，看了大佬的代码才明白过来。下面来看代码。

代码

class Pair{
    int fir,sec;
    Pair(int fir,int sec)
    {
        this.fir = fir;
        this.sec = sec;
    }
}
int stoneGame(int[] piles)
{
    int n = sizeof(piles) / sizeof(piles[0]);
    //初始化dp数组
    Pair[][] dp = new Pair[n][n];
    for(int i = 0;i < n;i++)
    {
        for(int j = i;j < n;j++)
        {
            dp[i][j] = new Pair(0,0);
        }
    }
    //输入base case
    for(int i = 0;i < n;i++)
    {
        dp[i][i].fir = piles[i];
        dp[i][i].sec = 0;
    }
    //斜着遍历数组
    //斜着遍历的时候,初始列的位置前面的格子数=遍历到末尾,所在行下面的格子数
    for(int l = 2;l <= n;l++)
    {
        for(int i = 0;i <= n - l;i++)
        {
            int j = i+l-1;
            //先手选择最左边或者最右边的分数
            int left = piles[i] + dp[i+1][j].sec;
            int right = piles[j] + dp[i][j-1].sec;
            //套用状态方程
            if(left > right)
            {
                dp[i][j].fir = left;
                //先手选完了,给我剩下了piles[i+1....j],我变成了这一堆里的先手
                dp[i][j].sec = dp[i+1][j].fir;
            }
            else
            {
                dp[i][j].fir = right;
                //先手选完了,给我剩下了piles[i....j-1],我变成了这一堆里的先手
                dp[i][j].sec = dp[i][j-1].fir;
            }
        }
    }
    Pair res = dp[0][n-1];
    return res.fir - res.sec;
}

总结

博弈问题的前提一般都是在两个聪明人之间进行的，编程描述这种游戏的一般方法是二维dp数组，数组中通过元组分别表示两人的最优决策。
之所以这样设计，是因为先手做出选择之后，就成了后手，后手在对方做出选择后，就变成了先手。这种角色转换使得我们可以重用之前的结果，典型的动态规划标志。
可能这里面存在着一些逻辑上的难点需要仔细思考。真正的博弈论问题不止这样，而要比这难上好多倍，但其实都是有确定规则公式的。倒是这种打着博弈问题的幌子，其实考察的是动态规划算法的问题才是最常见的。
好啦，这一次就到这里，下一次我会用一种动态规划的方法解决最让人头疼KMP问题，是的，你没听错，就是动态规划，一种不需要声明next数组就可以解决KMP问题的算法。