CF559A Gerald‘s Hexagon(几何)

CF559A Gerald’s Hexagon

题意：

按顺时针顺序给出一个六个内角全部都是$120°$的六边形六条边的边长,求该六边形剖分成三条边边长全部为$1$的等边三角形的个数.
保证该六边形能够剖分成若干个边长全部为$1$的等边三角形.

思路：

正面想递推很难推出公式，所以考虑直接求面积。
假设六条边分别为$a,b,c,d,e,f,g$。

• 可以考虑拆分成四个三角形，利用余弦和正弦定理求出六边形面积再除去一个小三角形的面积。

然而这种做法不可行，函数带来的精度误差还是比较大的。

观察题目，六个内角都是$120°$。可以考虑每隔两条边向外延长。

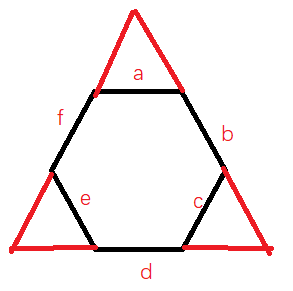
延长造成的三角形是等边的，大的三角形也是等边的。考虑用大的三角形减去延长产生的三个小三角形。

大的三角形面积：$S_1=(e+d+c)\ast (e+d+c)\ast 0.5\ast sin60°$
小的三角形面积：$S_2=e\ast e\ast 0.5\ast sin60°+c\ast c\ast 0.5\ast sin60°+a\ast a\ast 0.5\ast sin60°$
一个边长为1的等边三角形面积： $S_3=0.5\ast sin60°$

则答案为:$\frac{S_1-S_2}{S_3}$。

要注意的是要提前把式子中的$0.5\ast sin60°$手动约掉，不然会有精度误差。

Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll q[2000];
ll sum[2000];
/**
 * 几何
 */
const double pi=acos(-1);
int main(){ 
	long double q3=sqrt(3.0);
	long double a,b,c,d,e,f;
	cin>>a>>b>>c>>d>>e>>f;
	double s=(e+d+c)*(e+d+c);
	double s1=e*e;
	double s2=a*a;
	double s3=c*c;
	cout<<(ll)(s-s1-s2-s3);
	return 0;
}