[leetcode]112.路径总和-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_44699689/article/details/121037605

这篇博客介绍了如何在给定的二叉树中判断是否存在一条从根节点到叶子节点的路径，使得路径上的节点值之和等于给定的目标和。通过递归方法，遍历每个节点并检查其子节点是否能达成目标和。当遇到叶子节点时，直接比较当前路径和与目标和的大小。若找到匹配的路径，返回true，否则继续搜索。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。

叶子节点是指没有子节点的节点。

示例1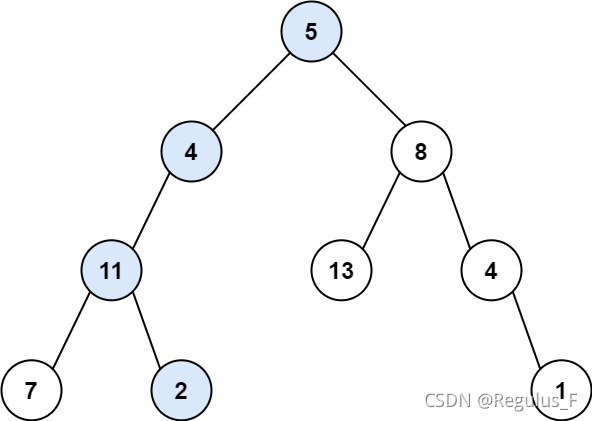：请添加图片描述

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true

示例2：
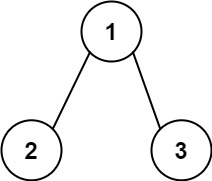
请添加图片描述

输入：root = [1,2,3], targetSum = 5
输出：[]

示例3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

思路：
从root节点到叶子节点的路径，满足其路径和为sum。
假定从根节点到当前路径和为val，那么就可以转换为求：是否存在从当前节点到叶子节点的路径，路径节点之和为sum-val。
如果当前节点是叶子节点，那么判断sum是否等于val即可，如果不是，则递归判断它的子节点是否可以满足条件。

AC代码：（C++）

class Solution {
   public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if (root == nullptr) return false;
        if (root->left == nullptr && root->right == nullptr) {
            return targetSum == root->val;
        }
        return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
    }
};