[leetcode]剑指 Offer 46. 把数字翻译成字符串

最新推荐文章于 2022-04-26 10:12:22 发布

RegulusF

最新推荐文章于 2022-04-26 10:12:22 发布

阅读量132

点赞数

分类专栏： LeetCode 文章标签： leetcode 动态规划 bash

本文链接：https://blog.youkuaiyun.com/weixin_44699689/article/details/120918632

版权

LeetCode 专栏收录该内容

237 篇文章

订阅专栏

该博客介绍了一种使用动态规划解决将数字翻译为特定字符串的方法。给定一个数字，根据特定规则将其翻译成字符串，例如0对应'a'，1对应'b'等。通过状态转移方程计算不同翻译方案的数量，代码示例中展示了如何实现这一过程，并给出了优化空间的策略，最终得出输入数字的翻译方案数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

给定一个数字，我们按照如下规则把它翻译为字符串：0 翻译成 “a” ，1 翻译成 “b”，……，11 翻译成 “l”，……，25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数，用来计算一个数字有多少种不同的翻译方法。

示例 1:

输入: 12258
输出: 5
解释: 12258有5种不同的翻译，分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"

提示：

0 <= num < 231

思路：（leetcode题解）
动态规划

在这里插入图片描述

定义dp数组，dp[i]表示以xi为结尾的数字的翻译方案数量。
状态转移方程：
若xi和xi-1组成的两位数字可以被翻译(可翻译的区间：[10,25])，则dp[i] = dp[i-1] + dp[i-2]，否则dp[i] = dp[i-1]
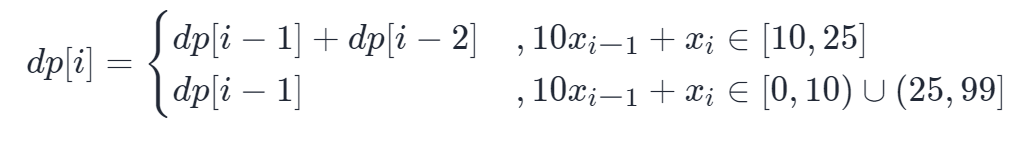
在这里插入图片描述

初始状态：

dp[0] = dp[1] = 1 （当 numnum 第 1, 21,2 位的组成的数字∈[10,25] 时，显然应有 2 种翻译方法，即 dp[2] = dp[1] + dp[0] = 2 ，而显然 dp[1] = 1 ，因此推出 dp[0] = 1。

将nums转换为字符串s，遍历s实现动态规划。

空间优化：由于只与dp[i]和dp[i-1]有关，可以仅用两个变量记录，交替前进即可。

AC代码：（C++）

class Solution {
   public:
    int translateNum(int num) {
        string str = to_string(num);
        int len = str.size();
        if (len < 2) {
            return len;
        }
        vector<int> dp(len + 1);
        int a = 1, b = 1, temp;
        for (int i = 2; i <= len; i++) {
            if ((str[i - 2] == '1') || (str[i - 2] == '2' && str[i - 1] <= '5')) {
                temp = a + b;
            } else {
                temp = a;
            }
            b = a;
            a = temp;
        }
        return a;
    }
};