java8种经典排序算法
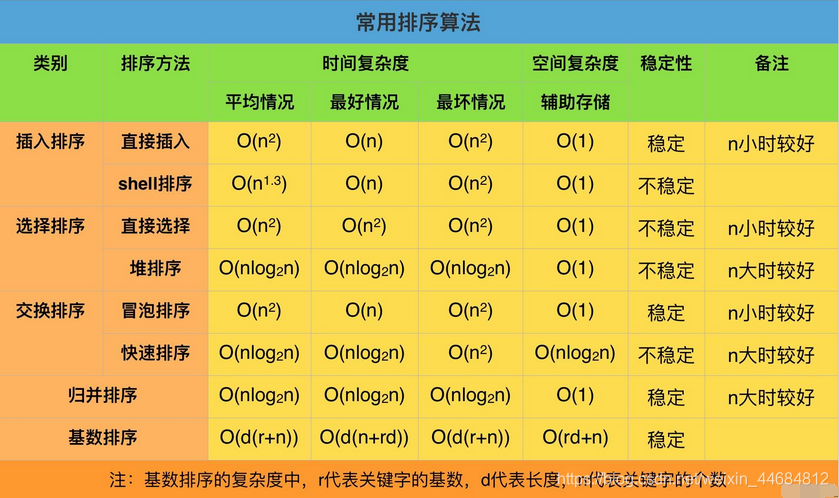
常用算法排序表
排序算法关系图
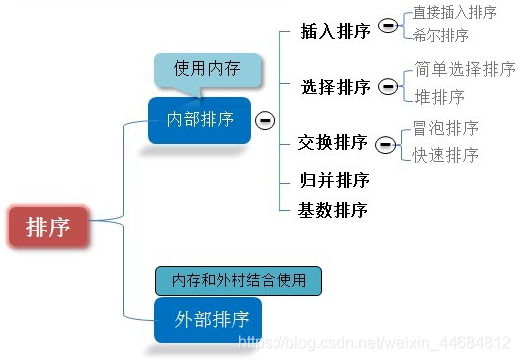
内部排序
- 内部排序是数据记录在内存中进行排序。
外部排序
- 外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
插入排序
直接插入排序
思想
- 直接插入排序是将未排序的数据插入到已经排序完成的苏列的对应位置,类似于扑克的排序。
- 比较数组的前两个数据并排序
- 第三个数据与前两个数据进行比较并排序。
- 依次类推直到排序完成。
实例
public static void fun(int[] a){
int temp;
for(int i = 1;i<a.lenght;i++){
temp = a[i];//带插入数据
int j =i-1;
while(j>0&&a[j]>temp){
a[j+1]=a[j]
j--;
}
a[j+1]=temp
}
}
算法分析(结合图一):
直接插入排序算法的空间复杂度为O(1)。
最好的情况,要比较的无序序列原本就是顺序有序的,那么要比较的次数是n-1,移动了0次,时间复杂度O(n)。最坏的情况,要比较的无序序列原本就是逆序有序的,那么要比较的次数是(n+2)(n-1)/2,移动的次数(n+4)(n-1)/2,时间复杂度O(n²)。
直接插入排序的平均复杂度为O(n²)。 直接插入排序是稳定的。
希尔排序
思想
- . 基于插入排序的思想,又被称为缩小增量排序
- 将包含n个元素的数组,分成n/2个数组序列,第一个数据和第n/2+1个数据为一对进行排序
- 然后分成成n/4个数组序列,继续排序。
//有些同学可能不理解我举个实例说一下
{10,9,6,3,7,11}
第一次排序分成6/2=3组分别为{10,3}{9,7}{6,11}
排序为{3,7,6,10,9,11}
第二次排序分为6/4=1(去浮点)继续插入排序两两对比
实例
public static void shell(int[] data) {
int j = 0;
int temp = 0;
for (int increment = data.length / 2; increment > 0; increment /= 2){
for (int i = increment; i < data.length; i++) {
temp = data[i];
for (j = i - increment; j >= 0; j -= increment) {
if (temp < data[j]) {
data[j + increment] =data[j];
} else {
break;
}
}
data[j + increment] = temp;
}
}
}
算法分析;
对于插入排序而言,如果原数组是基本有序的,那排序效率就可大大提高。另外,对于数量较小的序列使用直接插入排序,会因需要移动的数据量少,其效率也会提高。因此,希尔排序具有较高的执行效率。
希尔排序并不稳定,O(1)的额外空间,时间复杂度为O(n²)。
选择排序
简单选择排序
思想:每次确定一个最小值,从首项开始排序
- 对于给定的一组记录,经过第一轮比较后得到最小的记录,然后将该记录的位置与第一个记录的位置交换;接着对不包括第一个记录以外的其他记录进行第二次比较,得到最小记录并与第二个位置记录交换;重复该过程,知道进行比较的记录只剩下一个为止。
实例
for(int i= 0;i<a.length-1;i++){
for(iint j=1;j<a.length;j++)
if(a[i]>a[j]){
int temp = a[i];
a[i] =a[j];
a[j] =temp;
}
}
算法分析;
时间复杂度:假设有n个数据,数据交换的次数最多为n-1次,但程序的总体的比较次数较多。所以综合考虑有直接选择排序的时间复杂度为O(n2)(n的平方)。所以当记录占用字节数较多时,通常比直接插入排序的执行速度快些。空间复杂度:直接选择排序的空间复杂度很好,它只需要一个附加单元用于数据交换,所以其空间复杂度为O(1)。稳定性:由于在直接选择排序中存在着不相邻元素之间的互换,因此,直接选择排序是一种不稳定的排序方法。
堆排序
思想
什么是堆?
- 以前的博客有写堆和栈,今天再来回顾一下。
- 堆是一种特殊的树形数据结构,其每个节点都有一个值,通常提到的堆都是指一颗完全二叉树,根结点的值小于(或大于)两个子节点的值,同时,根节点的两个子树也分别是一个堆。
堆 - 堆排序是一种树形选择排序,是对直接选择排序的有效改进。
- 其排序是将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根节点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余的 n-1 个序列重新构造成一个堆,这样就会得到 n 个元素中次大的值。如此反复执行,便能得到一个有序序列了。
实例
给出一个初始的序列:{10,9,3,16,72}
1、建立一个堆,进行交换(从堆中剔除最大的数)
2、剩余的数据再次进行交换剔除最大的数知道最后两个数据进行交换
import java.util.Arrays;
public class Sort {
public static void main(String[] args) {
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
heapSort(a);
}
public static void heapSort(int[] a){
System.out.println("开始排序");
int arrayLength=a.length;
//循环建堆
for(int i=0;i<arrayLength-1;i++){
//建堆
buildMaxHeap(a,arrayLength-1-i);
//交换堆顶和最后一个元素
swap(a,0,arrayLength-1-i);
System.out.println(Arrays.toString(a));
}
}
private static void swap(int[] data, int i, int j) {
// TODO Auto-generated method stub
int tmp=data[i];
data[i]=data[j];
data[j]=tmp;
}
//对data数组从0到lastIndex建大顶堆
private static void buildMaxHeap(int[] data, int lastIndex) {
// TODO Auto-generated method stub
//从lastIndex处节点(最后一个节点)的父节点开始
for(int i=(lastIndex-1)/2;i>=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex<lastIndex){
//若果右子节点的值较大
if(data[biggerIndex]<data[biggerIndex+1]){
//biggerIndex总是记录较大子节点的索引
biggerIndex++;
}
}
//如果k节点的值小于其较大的子节点的值
if(data[k]<data[biggerIndex]){
//交换他们
swap(data,k,biggerIndex);
//将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的值
k=biggerIndex;
}else{
break;
}
}
}
}
}
//代码来自crazyYong博客
算法分析;
堆排序的运行时间主要耗费在初始构建堆和在重建堆时反复筛选上。
在构建对的过程中,因为我们是完全二叉树从最下层最右边的非终端节点开始构建,将它与其孩子进行比较和若有必要的互换,对每个非终端节点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次取堆顶记录重建堆需要用O(logi)的时间(完全二叉树的某个节点到根节点的距离为这里写图片描述),并且需要取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。
所以总体来说,堆排序的时间复杂度为O(nlogn),由于堆排序对原始记录的状态并不敏感,因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。
这在性能上显然要远远好过于冒泡、简单选择、直接插入的时间复杂度了。
空间复杂度上,它只有一个用来交换的暂存单元,也非常的不错。不过由于记录的比较与交换是跳跃式进行的,因此堆排序也是一种不稳定的排序方法。另外,由于出事构建堆所需要的比较次数比较多,因此,他并不适合待排序序列个数较少的情况。
交换排序
冒泡排序
思想
- 在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
- 冒泡法执行的次数是确定的,不存在最多和最少次数,如果有n个数要进行冒泡法排序,那么就要执行(n-1)+(n-2)+(n-3)……+3+2+1次循环!
实例
public int[] fun(int[] a){
for(int i = 0 ; i < a.length -1 ; i++ ){
for(int j = 0 ; j < a.length - i -1; j++){
if(a[j] > a[j+1]){
int temp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
return a;
}
快速排序
思想
- 选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
- 快速排序思想是来自冒泡排序,冒泡排序是通过相邻元素的比较和交换把最小的冒泡到最顶端,而快速排序是比较和交换小数和大数,这样一来不仅把小数冒泡到上面同时也把大数沉到下面。
- 冒泡+二分+递归分治
实例
- 在数组中选择一个基点,然后分别从数组两端进行扫描。
- 设置两个标准lo(起始位置)及hi(末尾)
- 先从后半部分扫描,现有元素比该基准点的值小,就交换lo和hi位置的值
- 后从前半部分开始扫秒,发现有元素大于基准点的值,就交换lo和hi位置的值。
- 直到循环到lo>=hi,然后把基准点的值放到hi这个位置。一次排序就完成了。
- 最后采用递归的方式进行前半部分和后半部分的排序直到完成。
- 假设你要排序的数组是A[1]~A[N].
- 首先任意选取一个数据(通常选用第一个数据)作为关键数据,然后将所有比它的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一躺快速排序。
算法解析
- 设置两个变量I、J,排序开始的时候I:=1,J:=N;
- 以第一个数组元素作为关键数据,赋值给X,即X:=A[1];
- 从J开始向前搜索,即由后开始向前搜索(J:=J-1),找到第一个小于X的值,两者交换;
从I开始向后搜索,即由前开始向后搜索(I:=I+1),找到第一个大于X的值,两者交换;
直到找到I=J结束
图解
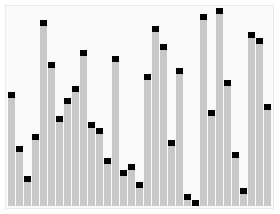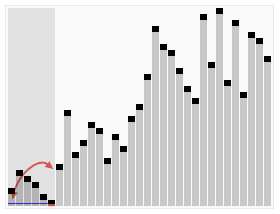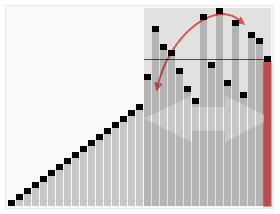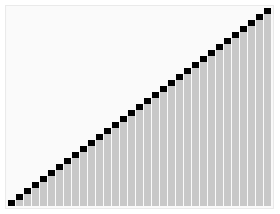
public class SortTest {
public static void main(String []args){
System.out.println("Hello World");
int[] a = {2,1,4,3};
int start = 0;
int end = a.length-1;
sort(a,start,end);
for(int i = 0; i<a.length; i++){
System.out.println(a[i]);
}
}
public static void sort(int[] a,int s_start,int s_end){
int start = s_start;
int end = s_end;
int key = a[s_start];
while(end>start){
//从后往前比较
while(end>start&&a[end]>=key) //如果没有比关键值小的,比较下一个,直到有比关键值小的交换位置,然后又从前往后比较
end--;
if(a[end]<=key){
int temp = a[end];
a[end] = a[start];
a[start] = temp;
}
//从前往后比较
while(end>start&&a[start]<=key)//如果没有比关键值大的,比较下一个,直到有比关键值大的交换位置
start++;
if(a[start]>=key){
int temp = a[start];
a[start] = a[end];
a[end] = temp;
}
//此时第一次循环比较结束,关键值的位置已经确定了。左边的值都比关键值小,
//右边的值都比关键值大,但是两边的顺序还有可能是不一样的,进行下面的递归调用
}
//递归
if(start>s_start) sort(a,s_start,start-1);//左边序列。第一个索引位置到关键值索引-1
if(end<s_end) sort(a,end+1,s_end);//右边序列。从关键值索引+1到最后一个
}
}
归并排序
思想
- 基本排序:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
- 充分利用了完全二叉树的深度是long2n+1的特性,使其效率比较高
实例
对于给定的一组记录,利用递归与分治技术将数据序列划分成为越来越小的半子表,在对半子表排序,最后再用递归方法将排好序的半子表合并成为越来越大的有序序列。
基数排序
思想
- 将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
- 选择排序、插入排序、快速排序等都是基于两个元素的比较进行排序的。而基数排序无需进行元素比较,基于队列处理就能够达到排序的目的。
- 基数排序不是基于排序关键字来比较排序项,而是基于排序关键字的结构。对于排序关键字中的每一个数字或字符的每一种可能取值,都会创建一个单独的队列。队列的数目就称为基数。
补充
为什么不是所有的排序都使用基数排序算法呢?
1.基数排序算法要根据给定问题特别设计;
2.如果排序关键字中的数字数目与列表中元素的数目接近,那么算法的时间复杂度接近O(n平方);
3.基数影响空间复杂度。
实例
import java.util.ArrayList;
import java.util.List;
public class radixSort {
public static void main(String[] args) {
int a[] = { 49, 38, 65, 97, 76, 13, 27, 49, 78, 34, 12, 64, 5, 4, 62,
99, 98, 54, 101, 56, 17, 18, 23, 34, 15, 35, 25, 53, 51 };
sort(a);
for (int i = 0; i < a.length; i++)
System.out.println(a[i]);
}
public static void sort(int[] array) {
// 首先确定排序的趟数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
int time = 0;
// 判断位数;
while (max > 0) {
max /= 10;
time++;
}
// 建立10个队列;
List<ArrayList> queue = new ArrayList<ArrayList>();
for (int i = 0; i < 10; i++) {
ArrayList<Integer> queue1 = new ArrayList<Integer>();
queue.add(queue1);
}
// 进行time次分配和收集;
for (int i = 0; i < time; i++) {
// 分配数组元素;
for (int j = 0; j < array.length; j++) {
// 得到数字的第time+1位数;
int x = array[j] % (int) Math.pow(10, i + 1)
/ (int) Math.pow(10, i);
ArrayList<Integer> queue2 = queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count = 0;// 元素计数器;
// 收集队列元素;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList<Integer> queue3 = queue.get(k);
array[count] = queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}
}
算法分析
- 在基数排序中,没有任何元素的比较和交换,元素只是在每一轮中从一个队列移动到另一个队列。
- 对于给定的基数,遍历数据的轮次是一个常数,它与排序关键字的数目无关,于是,基数排序算法的时间复杂度为O(n)。
致谢:https://blog.youkuaiyun.com/jackesy/article/details/80135033


























 393
393

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








