入门机器学习,首先要接触到的就是线性回归,里面包含的思想是后面机器学习的一个重要的基础。(ps:趁着简单,多琢磨琢磨)
一.最小二乘法拟和一元线性回归
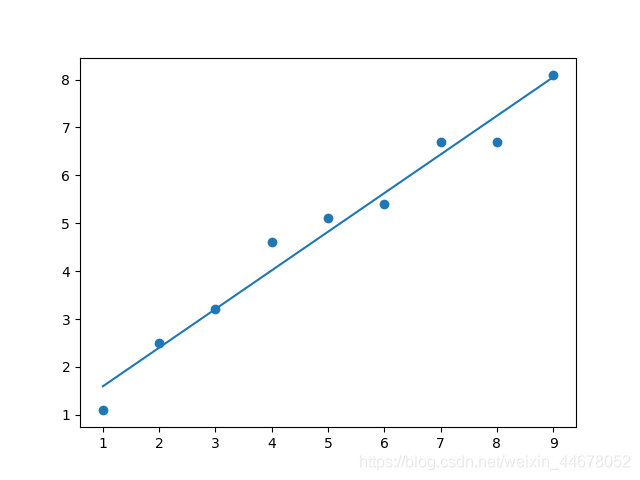
目标方程:y = wx + b,通过确定w,b来使得方程 E = ∑(y-wx-b)^2的值最小化
首先来对w,b分别求导,然后令导数为零,即可使得E的值最小,E被称为损失函数,又称为代价函数。求导过程很简单的,大家可以直接手动去求一下,代码里面也有w,b的表达式。
import matplotlib.pyplot as plt #导入绘图包
def main():
x = [1, 2, 3, 4, 5, 6, 7, 8, 9] # 样本x
y = [1.1, 2.5, 3.2, 4.6, 5.1, 5.4, 6.7, 6.7, 8.1] # 样本y
x_sum = 0 # x的总和
y_sum = 0 # y的总和
x2_sum = 0 # x的平方和
y2_sum = 0 # y的平方和
for i in range(len(x)):
x_sum += x[i]
y_sum += y[i]
x2_sum += x[i] * x[i]
y2_sum += y[i] * y[i]
x_mean = x_sum / float(len(x)) # x的平均值
y_mean = y_sum / float(len(y)) # y的平均值
x_y_sum = 0 # y(x-x_mean)求和
for i in range(len(x)):
x_y_sum += y[i] * (x[i] - x_mean)
w = x_y_sum / (x2_sum - (1.0 / len(x)) * x_sum * x_sum) # 求解w
b = y_mean - w * x_mean # 求解 b
y_pred = []
for i in x:
y_pred.append(w*i+b)
plt.scatter(x,y) #绘图
plt.plot(x, y_pred)
plt.show()
if __name__ == '__main__':
main()
下面是c++的实现,基本和python差不多,适合新手。
#include <iostream>
using namespace std;
int main(void)
{
int i;
double w, b; //需要拟和的系数
double x[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
double y[] = { 1.1, 2.5, 3.2, 4.6, 5.1, 5.4, 6.7, 6.7, 8.1 };
double x_sum = 0, y_sum = 0, x2_sum = 0, y2_sum = 0, x_mean = 0, y_mean = 0, x_y_sum = 0;
for (i = 0; i < 9; i++)
{
x_sum += x[i], y_sum += y[i];
x2_sum += x[i] * x[i], y2_sum += y[i] * y[i];
}
x_mean = x_sum / 9.0;
y_mean = y_sum / 9.0;
for (i = 0; i < 9; i++)
x_y_sum += y[i] * (x[i] - x_mean);
w = x_y_sum / (x2_sum - (1.0 / 9)*x_sum*x_sum);
b = y_mean - w * x_mean;
return 0;
}
二.梯度下降法
在高中的时候,我们学过,函数在某一个区间内的导数大于零的话,函数值递增,否则递减。
只要我们每次利用当前的x减去这一点的导数值,就可以使得函数值减小。但为了更新后的x值不发生太大变化,往往还要给定一个学习率,来控制x的更新大小。
一个公式总结:new_x = x - 学习率 * ▽x
x = [1, 2, 3, 4, 5, 6, 7, 8, 9] # 样本x
y = [1.1, 2.5, 3.2, 4.6, 5.1, 5.4, 6.7, 6.7, 8.1] # 样本y
# 拟和方程为: y = 0.8*x + 0.8
w = 5 #随机初始化w
b = 3 #随机初始化b
loss = 0
for i in range(1000): #更新w,b的次数
w_D = 0
b_D = 0
loss = 0
for a in range(len(x)):
loss += (y[a] - (w*x[a]+b))**2
w_D -=(y[a]-(w*x[a]+b))*x[a] #得到函数对w的偏导数值
b_D +=w*x[a] + b - y[a] #得到函数对b的偏导数值
print('loss:%.2f'%loss)
w = w - 0.002*w_D #更新w 0.002为学习率
b = b - 0.002*b_D #更新b
print('w:%.2f'%w)
print('b:%.2f'%b)
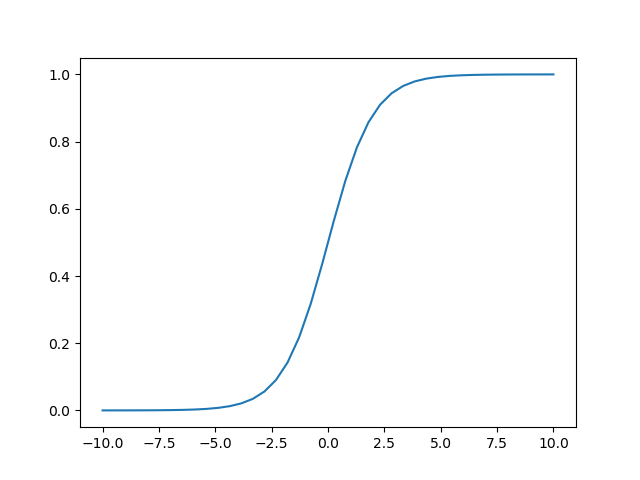
三.在回归的基础上,实现分类任务,要用到sigmoid函数来实现特征映射,函数图如下。代码没有用到矩阵的内容,容易理解,,照顾新手。
import matplotlib.pyplot as plt
import math
def sigmoid(x):
a =1.0/(1+ math.exp(-x))
if a>0.5:
return 1
else:
return 0
def main():
x = [0,1,2.1, 2,4.6, 3, 4, 5, 6, 7, 8, 9,10,12,14,15,16,17,21,22,23,24,25,26] # 样本x
y = [0,0, 0,0, 0,0, 0, 0, 1, 1, 1, 1,1,1,1,1,1,1,1,1,1,1,1,1] # 样本y 表示类别
w = 5 #初始化w,b,
b = 3
loss = 0
for i in range(1000):
w_D = 0
b_D = 0
loss = 0
for a in range(len(x)):
loss += (y[a] - sigmoid(w*x[a]+b))**2
w_D += -1*(y[a] - sigmoid(w*x[a]+b)) *x[a]
b_D += -1*(y[a] - sigmoid(w*x[a]+b))
print('loss:%.2f'%loss)
w = w - 0.2*(w_D)
b = b - 0.2*(b_D)
print(w_D)
print('w:%.2f'%w)
print('b:%.2f'%b)
a = sigmoid(w *7+ b)
print("%.2f"%a)
if __name__ == '__main__':
main()
在这里相信大家对最小二乘法和梯度下降法来拟和一元回归和分类有了一定的了解。那么趁热打铁,多项式回归又改如何呢?

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










