验证二叉搜索树BST
leetcode98
中序遍历,如果有降序就不是
class Solution {
long preValue = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null)
return true;
boolean isLeft = isValidBST(root.left);
if(!isLeft)
return false;
if(preValue >= root.val){
return false;
}
else
preValue = root.val;
return isValidBST(root.right);
}
}
验证完全二叉树
定义:只有最后一层不满
BFS
只有右节点,无左节点;
在1前提下,若遇到左右节点不全,则后续节点都得为叶节点
public boolean isCST(TreeNode root){
if(root == null)
return true;
//判断是否遇到子节点不全得情况
boolean leaf = false;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
root = queue.poll();
TreeNode left = root.left;
TreeNode right = root.right;
//遇到情况判断是否为叶节点
if((leaf && (left != null || right != null))
||
//判断左节点为空,右节点非空
(left == null && right != null)
)
return false;
if(left != null)
queue.add(left);
if(right != null)
queue.add(right);
if(left == null || right == null)
leaf = true;
}
return true;
}
验证平衡二叉树
定义:任何子树,左右子树高度差不能超过 1,左右子树都平衡
从下往上遍历,如果子树是平衡二叉树,则返回子树的高度;如果发现子树不是平衡二叉树,则直接停止遍历,这样至多只对每个结点访问一次。
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
return height(root) != -1;
}
public int height(TreeNode root){
if(root == null)
return 0;
int left = height(root.left);
if(left == -1)
return -1;
int right = height(root.right);
if(right == -1)
return -1;
return Math.abs(left - right) > 1 ? -1 : Math.max(left,right) + 1;
}
}
验证对称二叉树
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null)
return true;
return dfs(root.left,root.right);
}
public boolean dfs(TreeNode n1,TreeNode n2){
if(n1 == null && n2 == null)
return true;
if(n1 == null || n2 == null)
return false;
return n1.val == n2.val && dfs(n1.left,n2.right) && dfs(n1.right,n2.left);
}
}
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null || (root.left==null && root.right==null)) {
return true;
}
//用队列保存节点
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
//将根节点的左右孩子放到队列中
queue.add(root.left);
queue.add(root.right);
while(queue.size()>0) {
//从队列中取出两个节点,再比较这两个节点
TreeNode left = queue.removeFirst();
TreeNode right = queue.removeFirst();
//如果两个节点都为空就继续循环,两者有一个为空就返回false
if(left==null && right==null) {
continue;
}
if(left==null || right==null) {
return false;
}
if(left.val!=right.val) {
return false;
}
//将左节点的左孩子, 右节点的右孩子放入队列
queue.add(left.left);
queue.add(right.right);
//将左节点的右孩子,右节点的左孩子放入队列
queue.add(left.right);
queue.add(right.left);
}
return true;
}
}
验证满二叉树
所有节点个数 = 1 << 树的最大深度 - 1 = 2 ^ height - 1;
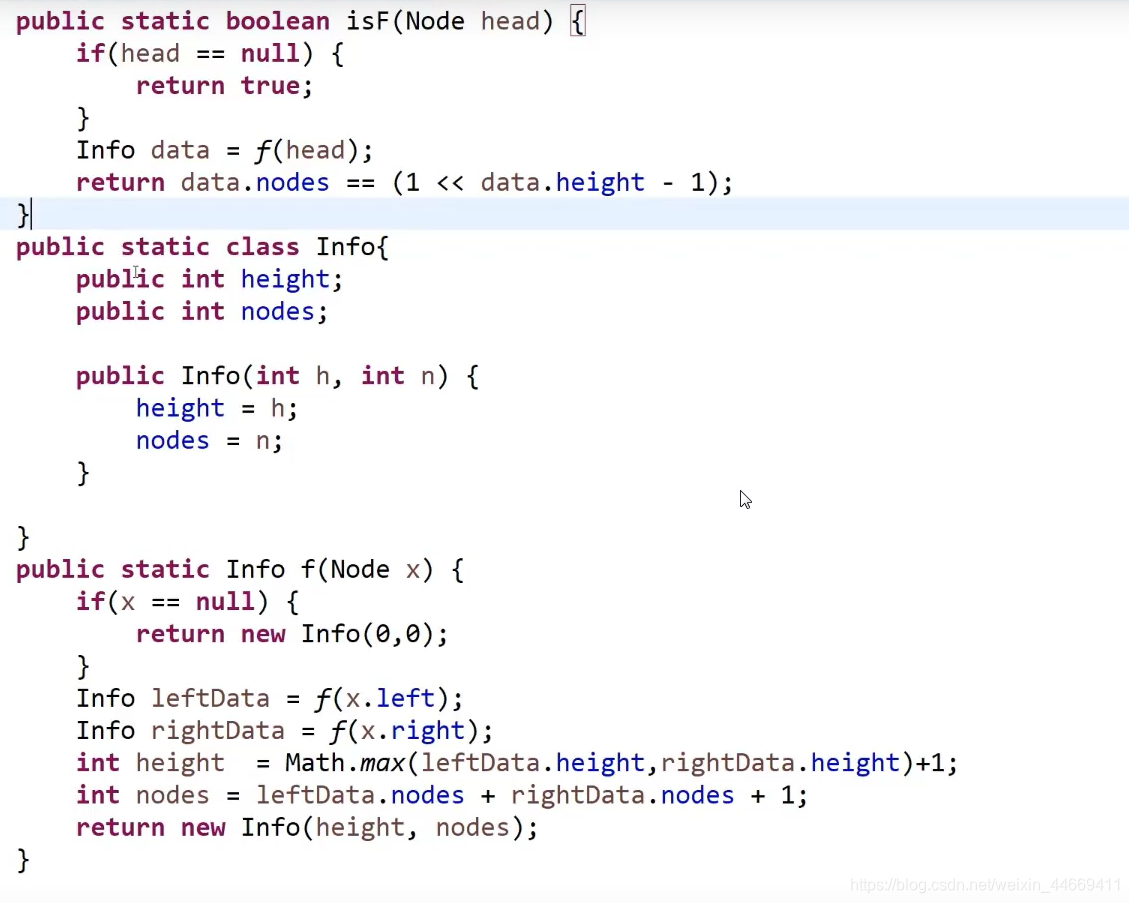








 这篇博客介绍了如何验证四种不同类型的二叉树:二叉搜索树(BST)通过中序遍历判断;完全二叉树使用BFS检查;平衡二叉树通过自底向上遍历确保子树高度差不超过1;对称二叉树的验证则关注左右子树的镜像关系;最后,满二叉树的验证利用其节点数与最大深度的关系。
这篇博客介绍了如何验证四种不同类型的二叉树:二叉搜索树(BST)通过中序遍历判断;完全二叉树使用BFS检查;平衡二叉树通过自底向上遍历确保子树高度差不超过1;对称二叉树的验证则关注左右子树的镜像关系;最后,满二叉树的验证利用其节点数与最大深度的关系。
















 1254
1254

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








