【汉诺塔问题】(Python)

什么是汉诺塔？

那么我们假设有n个盘子，移动方式如下:

通过上图我们想从简单理解一下逻辑，下面我们用一个简单的算法演示一下

假设有两个盘子，ABC三个柱子应该怎样移动

def hanoi(n,a,b,c):
    if n > 0:
        hanoi(n-1,a,c,b)
        print("moving from %s to %s" %(a,c))
        hanoi(n-1,b,a,c)

hanoi(2,'A','B','C')

n为盘子数，ABC分别代表三个柱子，运行结果如下:

两个盘子可以简单理解为一大一小，先将小的移动到B，再将大的移动到C，最后将B上小的移动到C，这样便完成了移动

那么我们再假设有三个盘子，用画图的方式详细演示一下

代码只需将调用改为3即可

def hanoi(n,a,b,c):
    if n > 0:
        hanoi(n-1,a,c,b)
        print("moving from %s to %s" %(a,c))
        hanoi(n-1,b,a,c)

hanoi(3,'A','B','C')

结果如下：

我们用大中小表示三个圆盘

第一步将小圆盘移动到c

 将中圆盘移动到b

将小圆盘移动到b 将大圆盘移动到c

将小圆盘移动到a

 

将中圆盘移动到c

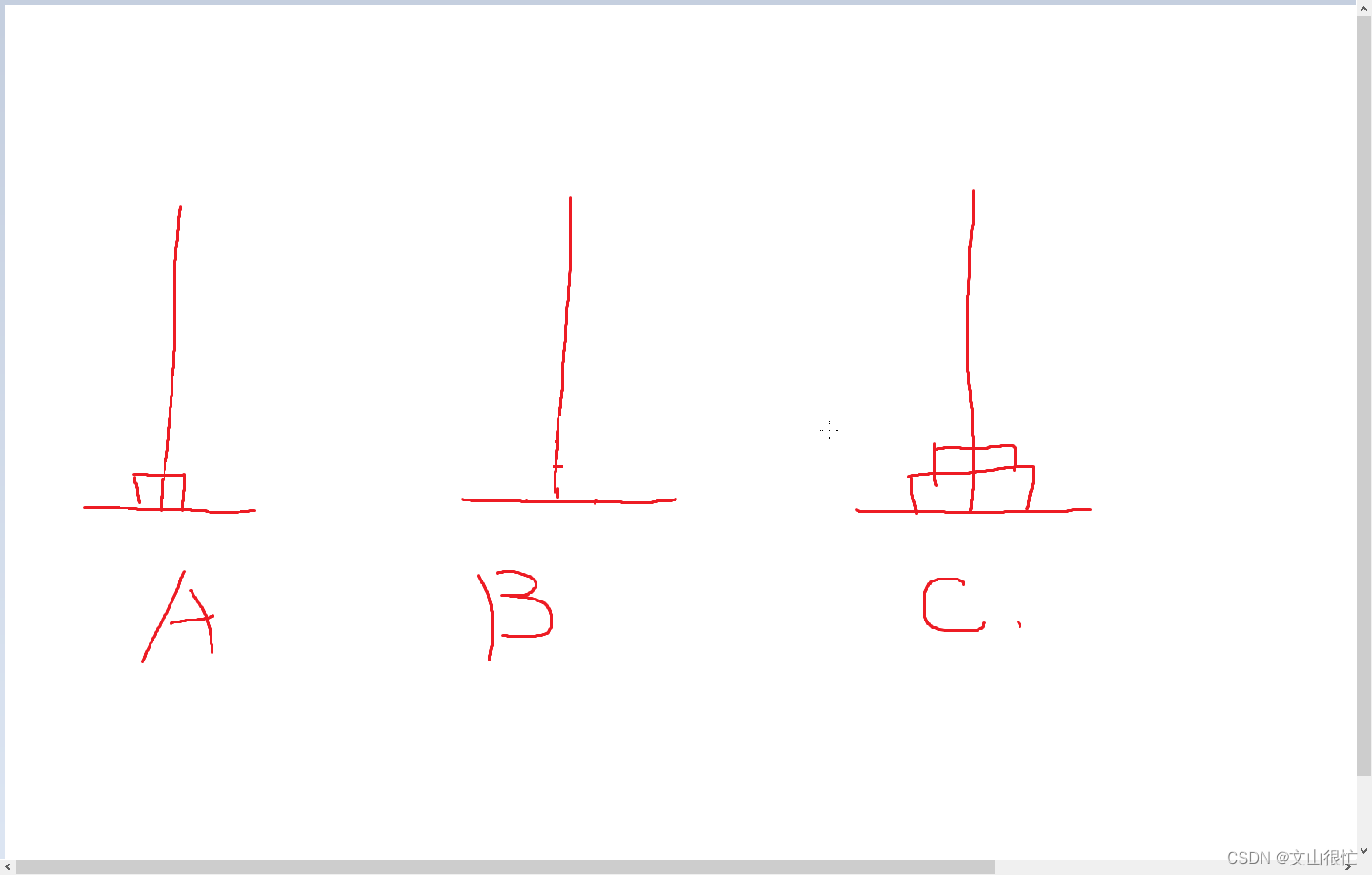 将小圆盘移动到c

由此我们可以推导出一个移动次数公式：

当有n个盘子时：

 h(n)=2h(n-1)+1

h(64)=18446744073709551615

假设婆罗门每秒搬一个盘子，则总共需要5800亿年

由此看来世界真的会毁灭