2019.8.9 JZ DAY9总结

今天由于题目较水，虽然分数很低，但是改题很快，下午三点半左右已经改完全部题目。

$T1$

$走格子$

Description

Input

Output

Sample Input
Sample 1:
4 4

#.F#
#C.#

Sample 2:
6 8
########
#.##…F#
#C.##…#
#…#…#
#…##
########

Sample 3:

#C#.#
###F#

Sample Output
Sample 1:
2

Sample 2:
4

Sample 3:
no

Data Constraint

Hint

看完全部题目后感觉这题不是道水题吗，好像爆搜都可以过，然后为了保险，就嗖嗖嗖地打了一个spfa，而后85pts。一脸懵逼，竟然是因为连边连错了，在任意一个点都要连一条边向四周的墙，边权为向四周墙的最短距离。虽然很有道理，但是感觉不连也没什么大问题鸭。

#include <cstdio>
#include <queue>
using namespace std;

const int N = 510;
const int dx[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};
struct Node
{
	int to,next,val;	
} f[10000100];
int n,m,map[N][N],cnt,head[N * N],dis[N * N],st,ed;
char ch[N];
bool vis[N * N];

queue <int> q;

bool check(int x,int y)	{if (x > 0 && x <= n && y > 0 && y <= m && map[x][y]) return 1; else return 0;}

int pl(int x,int y) {return (x - 1) * m + y;}

void add(int u,int v,int w)
{
	f[++ cnt].to = v;
	f[cnt].val = w;
	f[cnt].next = head[u];
	head[u] = cnt;
}

void BFS(int x,int y)
{
	int len,mi = N * N,H[5],cnt = 0;
	for (int i = 0,xx,yy; i <= 3; i ++)
	{
		len = 0;
		xx = x,yy = y;
		while (check(xx + dx[i][0],yy + dx[i][1])) xx += dx[i][0],yy += dx[i][1],++ len;
		len ++;
		if (len < mi) mi = len;
		if (x != xx || y != yy)H[++ cnt] = pl(xx,yy);
	}
	for (int i = 1; i <= cnt; i ++) add(pl(x,y),H[i],mi);
}

void SPFA()
{
	q.push(st);
	dis[st] = 0;
	while (!q.empty())
	{
		int u = q.front();
		q.pop();
		vis[u] = 0;
		for (int i = head[u],v; i; i = f[i].next)
		{
			v = f[i].to;
			if (dis[v] > dis[u] + f[i].val)
			{
				dis[v] = dis[u] + f[i].val;
				if (!vis[v]) vis[v] = 1,q.push(v);
			}
		}
	}
}

int main()
{
	freopen("portal.in","r",stdin);
	freopen("portal.out","w",stdout);
	cnt = 0;
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i ++)
	{
		scanf(" %s",ch);
		for (int j = 0; j < m; j ++)
			if (ch[j] == '#') map[i][j + 1] = 0;
		 	else if (ch[j] == '.') map[i][j + 1] = 1;
		 	else if (ch[j] == 'C') map[i][j + 1] = 1,st = pl(i,j + 1);
		 	else if (ch[j] == 'F') map[i][j + 1] = 1,ed = pl(i,j + 1);
	}
	for (int i = 1; i <= n; i ++)
		for (int j = 1; j <= m; j ++)
		{
			dis[pl(i,j)] = 10000100;
			if (map[i][j])
			{
				for (int k = 0; k <= 3; k ++)
					if (check(i + dx[k][0],j + dx[k][1])) add(pl(i,j),pl(i + dx[k][0],j + dx[k][1]),1);
				BFS(i,j);
			}
		}
	SPFA();
	if (dis[ed] == 10000100) printf("nemoguce"); else printf("%d",dis[ed]);
	return 0;
}

---

$T2$

$扭动的树$

Description

Input

Output

Sample Input
Sample 1
4
2 3
6 4
9 8
12 1

Sample 2
20
64978574415886122 263411
40589037247202745 239844
19724737874528206 167360
49216095485959384 760606
65063121727264647 659450
16572376111094320 726552
72014092598616298 133699
52843699826658793 427487
43374492289647376 552030
22047612465142862 605387
92386136280598953 718860
6436388687842008 368771
87727847161227820 880866
43622103777719758 352810
36870904328895185 322737
48993192459657624 456880
93250693206986868 619976
77407991580158822 861256
974508361120026 344635
77136053229840400 465474

Sample Output
Sample1:
51

Sample2:
101007480

Data Constraint

额考场完全没有思路因为自己错误地想法。我一直想着在树上做，然后就开始纠结左右儿子什么乱七八糟的东西，可是考后听了大佬讲解才明白可以将其转化为线性的问题。首先按照key值从小到大排序，然后对于每一个区间l，r，枚举一下fa，然后用记搜随便搞搞就过了，注意合并的时候的细节。

#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 330;
struct Node{
	long long key;
	int val;
} f[N];
int n,mp[N][N];
long long sum[N],g[N][N][2];

bool cmp(Node a,Node b) {return a.key < b.key;} 

long long gcd(long long a,long long b) {return a % b == 0 ? b : gcd(b,a % b);}

long long dfs(int l,int r,int fa)
{
	if (l > r) return 0;
	if (g[l][r][fa] != 0) return g[l][r][fa];
	long long res = 0;
	int x;
	bool p = 0;
	if (fa) x = r + 1; else x = l - 1;
	for (int i = l; i <= r; i ++)
	{
		if (!mp[i][x]) continue;
		long long s1 = dfs(l,i - 1,1),s2 = dfs(i + 1,r,0);
		if (s1 == -1 || s2 == -1) continue;
		if (s1 + s2 > res) res = s1 + s2;
		p = 1;
	}
	if (!p) return g[l][r][fa] = -1;
	return g[l][r][fa] = res + sum[r] - sum[l - 1];
}

int main()
{
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d",&n);
	for (int i = 1; i <= n; i ++)
		scanf("%lld%d",&f[i].key,&f[i].val);
	sort(f + 1,f + 1 + n,cmp);
	for (int i = 1; i <= n; i ++)
		sum[i] = sum[i - 1] + f[i].val;
	for (int i = 1; i <= n; i ++)
	{
		mp[i][0] = mp[0][i] = 1;
		for (int j = i + 1; j <= n; j ++)
			if (gcd(f[i].key,f[j].key) != 1) mp[i][j] = mp[j][i] = 1;
	}
	printf("%lld",dfs(1,n,0));
	return 0;
}

---

$T3$

$旋转子段$

Description

Input

Output

Sample Input
Sample 1:
4
3 2 1 4

Sample 2:
2
1 2

Sample Output
Sample 1:
4

Sample 2:
2

Data Constraint

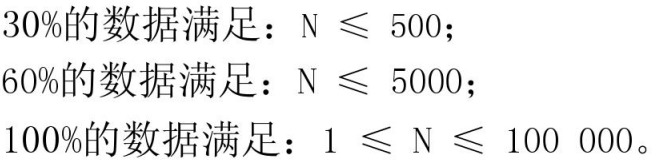
Hint

考场打了一个60pts 的暴力，枚举旋转中心然后一步步向外拓展，结果因为自己把文件操作注销掉了，导致爆零。正解就是一个先分别从前往后从后往前记录前缀和（有多少个点本来就是固定点），然后对于任意一个元素显然只有唯一一个旋转中心可以将其变为固定点没然后就是一波O（N）操作，就ok了。

#pragma GCC optimize(3)
#pragma GCC optimize(2)
#include <cstdio>
using namespace std;

const int N = 1e5 + 10;
int n,a[N],fr[N],bk[N],f[N << 1],ans,b[N];

int max(int a,int b) {return a > b ? a : b;}

int main()
{
	freopen("rotate.in","r",stdin);
	freopen("rotate.out","w",stdout);
	scanf("%d",&n);
	for (int i = 1; i <= n; i ++)
		scanf("%d",&a[i]),fr[i] = fr[i - 1] + (a[i] == i),b[a[i]] = i;
	for (int i = n; i >= 1; i --)
		bk[i] = bk[i + 1] + (a[i] == i);
	for (int i = 1; i <= n; i ++)
	{
		if (a[i] <= i)
			ans = max(ans,fr[a[i] - 1] + bk[i + 1] + (++ f[a[i] + i]));
		if (b[i] <= i && (a[i] != i || b[i] != i))
			ans = max(ans,fr[b[i] - 1] + bk[i + 1] + (++ f[b[i] + i]));
	}
	printf("%d",ans);
}

因为粗心今天分数又很低啊，努力