2021年秋季PAT甲级考试满分题解

7-1 Arrays and Linked Lists (20 分)

Let’s design a data structure $A$ that combines arrays and linked lists as the following:

At the very beginning, an integer array $A_0$ of length $L_0$ is initialized for the user. When the user tries to access the ith element $A[i]$, if $0\le i<L_0$, then $A[i]$ is just $A_0[i]$. Now our system is supposed to return $h_0+i\times sizeof(int)$ as the accessed address, where $h_0$ is the initial address of $A_0$, and $sizeof(int)$ is the size of the array element, which is simply int, taking 4 bytes.

In case there is an overflow of the user’s access (that is, $i\ge L_0$), our system will declare another array $A_1$ of length $L_1$. Now $A[i]$ corresponds to $A_1[j]$ (It’s your job to figure out the relationship between $i$ and $j$). If $0\le j<L_1$, then $h1+j\times sizeof(int)$ is returned as the accessed address, where $h_1$ is the initial address of $A_1$.

And if there is yet another overflow of the user’s access to $A_1[j]$, our system will declare another array $A_2$ of length $L_2$, and so on so forth.

Your job is to implement this data structure and to return the address of any access.

Input Specification:

Each input file contains one test case. For each case, the first line gives 2 positive integers $N$ (≤104) and $K$ (≤103) which are the number of arrays that can be used, and the number of user queries, respectively.

Then $N$ lines follow, each gives 2 positive integers, which are the initial address (≤107) and the length (≤100) of an array, respectively. The numbers are separated by spaces. It is guaranteed that there is no overlap of the spaces occupied by these arrays.

Finally, $K$ indices of the elements queried by users are given in the last line. Each index is an integer in the range [0,220].

Output Specification:

For each query, print in a line the accessed address. If the queried index exceeds the range of all the N arrays, output Illegal Access instead, and this query must NOT be processed.

Print in the last line the total number of arrays that have been declared for the whole process.

Sample Input:

6 7
2048 5
128 6
4016 10
1024 7
3072 12
9332 10
2 12 25 50 28 8 39

Sample Output:

2056
4020
1040
Illegal Access
3072
140
3116
5

分析：

本题是这套题唯一有坑点的地方，需要注意刚开始默认就有数组$A_0$，之后按顺序创建。

Code：

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n, k, maxn = 0, address, key, temp, no = 0, cnt = 1;
    scanf("%d %d", &n, &k);
    vector<pair<int, int>> arrays;
    vector<int> large(n, 0);
    vector<int> visit(n, 0);
    for (int i = 0; i < n; i++) {
        scanf("%d %d", &address, &key);
        maxn += key;
        large[i] = key;
        if (i != 0)large[i] += large[i - 1];
        arrays.push_back({address, key});
    }
    vector<int> nums(maxn, 0);
    for (int i = 0; i < maxn; i++) {
        if (i < large[no]) {
            nums[i] = no;
        } else {
            no++;
            nums[i] = no;
        }
    }
    while (k > 0) {
        k--;
        scanf("%d", &temp);
        if (temp >= maxn) {
            printf("Illegal Access\n");
            continue;
        } else {
            int pos;
            int t = nums[temp];
            visit[t] = 1;
            if (t != 0)pos = temp - large[t - 1];
            else pos = temp;
            printf("%lld\n", arrays[t].first + 4 * pos);
        }
    }
    for (int i = n - 1; i >= 1; i--) {
        if (visit[i] == 1) {
            cnt = i + 1;
            break;
        };
    }

    printf("%d", cnt);
    return 0;
}

7-2 Stack of Hats (25 分)

PATers believe that wearing hats makes them look handsome, so wherever they go, everyone of them would wear a hat. One day they came to a restaurant, a waiter collected their hats and piled them up. But then when they were ready to leave, they had to face a stack of hats as shown by the above figure. So your job is to help them line up so that everyone can pick up his/her hat one by one in order without any trouble.

It is known that every hat has a unique size, which is related to the weight of its owner – that is, the heavier one wears larger hat.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive number N (≤104) which is the number of PATers. The next line gives N distinct sizes of the hats, which are positive numbers no more than 105. The sizes correspond to the hats from bottom up on the stack. Finally in the last line, N distinct weights are given, correspond to the hat owners numbered from 1 to N. The weights are positive numbers no more than 106. All the numbers in a line are separated by spaces.

Output Specification:

For each test case, print in a line the indices of the hat owners in the order of picking up their hats. All the numbers must be separated by exactly 1 space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
12 19 13 11 15 18 17 14 16 20
67 90 180 98 87 105 76 88 150 124

Sample Output:

3 4 8 6 10 2 1 5 9 7

Hint:

The 1st hat has the largest size 20, hence must correspond to the one with the largest weight, which is the 3rd one of weight 180. So No.3 must go first.

The 2nd hat has the 6th smallest size 16, hence corresponds to the 6th smallest weight, which is 98. So No.4 is the next to go.

And so on so forth.

分析：

排序和哈希表，非常简单。

Code：

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n;
    scanf("%d", &n);
    unordered_map<int, int> hatsize, people, weightsize;
    vector<int> hat(n, 0), weight(n, 0), res;
    for (int i = 0; i < n; i++) {
        scanf("%d", &hat[i]);
    }
    for (int i = 0; i < n; i++) {
        scanf("%d", &weight[i]);
    }
    vector<int> nums1 = hat, nums2 = weight;
    sort(nums1.begin(), nums1.end());
    sort(nums2.begin(), nums2.end());
    for (int i = 0; i < n; i++) {
        hatsize[nums1[i]] = i;
        people[weight[i]] = i;
        weightsize[i] = nums2[i];
    }
    for (int i = n - 1; i >= 0; i--) {
        int h = hat[i];
        int l1 = hatsize[h];
        int cp = weightsize[l1];
        res.push_back(people[cp]);
    }
    for (int i = 0; i < res.size(); i++) {
        if (i != 0)printf(" ");
        printf("%d", res[i] + 1);
    }
    return 0;
}

7-3 Playground Exploration (25 分)

A playground is equipped with ball pits and tents connected by tunnels. Kids can crawl through the tunnels to meet their friends at a spot with a tent or a ball pit.

Now let’s mark each meeting spot (a tent or a ball pit) by a number. Assume that once a kid starts to explore the playground from any meeting spot, he/she will always choose the next destination with the smallest number, and he/she would never want to visit the same spot twice. Your job is to help the kids to find the best starting spot so they can explore as many spots as they can.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤100), the total number of spots, and M, the number of tunnels. Then M lines follow, each describes a tunnel by giving the indices of the spots (from 1 to N) at the two ends.

Output Specification:

Print in a line the best starting spot which leads to the maximum number of spots, and the number of spots a kid can explore. If the solution is not unique, output the one with the smallest index. There must be exactly 1 space between the two numbers, and there must be no extra space at the beginning or the end of the line.

Sample Input:

8 10
1 2
3 4
5 8
1 4
6 1
3 7
2 4
5 3
2 8
2 5

Sample Output:

6 7

Hint:

Actually there are two solutions. Kids can either start from 6 and go through 1->2->4->3->5->8, or from 7 to 3->4->1->2->5->8, both can visit 7 spots. Since 6 is a smaller index, we output 6 as the starting spot.

分析：

每次都会找到未访问过的最小号码的目的地，即可以直接使用dfs回溯

Code：

#include <bits/stdc++.h>

using namespace std;

vector<vector<int>> v;
int visit[105];
int n, m, maxn = 0, node = -1, flag = 1;

void dfs(int start, int pos, int no) {
    if (!flag)return;
    int isend = 0;
    if (no > maxn) {
        maxn = no;
        node = start;
    }
    for (int i = 0; i < v[pos].size(); i++) {
        if (!visit[v[pos][i]]) {
            isend = 1;
            visit[v[pos][i]] = 1;
            dfs(start, v[pos][i], no + 1);
            visit[v[pos][i]] = 0;
        }
    }
    if (isend == 0) {
        flag = 0;
    }
}

int main() {
    int a, b;
    scanf("%d %d", &n, &m);
    v.resize(n + 1);
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &a, &b);
        v[a].push_back(b);
        v[b].push_back(a);
    }
    for (int i = 1; i <= n; i++) {
        sort(v[i].begin(), v[i].end());
    }
    for (int i = 1; i <= n; i++) {
        flag = 1;
        visit[i] = 1;
        dfs(i, i, 1);
        visit[i] = 0;
        if (maxn == n)break;
    }
    printf("%d %d", node, maxn);
    return 0;
}

7-4 Sorted Cartesian Tree (30 分)

A Sorted Cartesian tree is a tree of (key, priority) pairs. The tree is heap-ordered according to the priority values, and an inorder traversal gives the keys in sorted order. For example, given the pairs { (55, 8), (58, 15), (62, 3), (73, 4), (85, 1), (88, 5), (90, 12), (95, 10), (96, 18), (98, 6) }, the increasing min-heap Cartesian tree is shown by the figure.

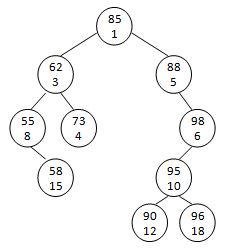
Your job is to do level-order traversals on an increasing min-heap Cartesian tree.

Input Specification:

Each input file contains one test case. Each case starts from giving a positive integer N (≤30), and then N lines follow, each gives a pair in the format key priority. All the numbers are in the range of int.

Output Specification:

For each test case, print in the first line the level-order traversal key sequence and then in the next line the level-order traversal priority sequence of the min-heap Cartesian tree.

All the numbers in a line must be separated by exactly one space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

10
88 5
58 15
95 10
62 3
55 8
98 6
85 1
90 12
96 18
73 4

Sample Output:

85 62 88 55 73 98 58 95 90 96
1 3 5 8 4 6 15 10 12 18

分析：

本题要求求出排序笛卡尔树，可以注意到他是符合最小堆的性质，其中序遍历满足从小大的顺序。因此可以使用节点存储key和value，然后对value进行排序。根据性质一个一个插入结点，最后层序遍历即可。

Code：

#include <bits/stdc++.h>

using namespace std;

struct node {
    int key, value;
};

vector<node> nodes;

bool cmp(node n1, node n2) {
    if (n1.value != n2.value)return n1.value < n2.value;
    else return n1.key < n2.key;
}

struct TreeNode {
    node val;
    TreeNode *left, *right;

    TreeNode(node val) : val(val), left(nullptr), right(nullptr) {}
};

TreeNode *buildMyTree(TreeNode *root, node val) {
    if (root == nullptr)root = new TreeNode(val);
    else {
        if (root->val.key > val.key)root->left = buildMyTree(root->left, val);
        else root->right = buildMyTree(root->right, val);
    }
    return root;
}

int main() {
    int n, key, value;
    scanf("%d", &n);
    vector<node> res;
    for (int i = 0; i < n; i++) {
        scanf("%d %d", &key, &value);
        nodes.push_back({key, value});
    }
    sort(nodes.begin(), nodes.end(), cmp);
    TreeNode *root = nullptr;
    for (int i = 0; i < n; i++) {
        root = buildMyTree(root, nodes[i]);
    }
    queue<TreeNode *> q;
    if (root != nullptr)q.push(root);
    while (!q.empty()) {
        int currentSize = q.size();
        for (int i = 0; i < currentSize; i++) {
            auto node1 = q.front();
            res.push_back(node1->val);
            q.pop();
            if (node1->left != nullptr)q.push(node1->left);
            if (node1->right != nullptr)q.push(node1->right);
        }
    }
    for (int i = 0; i < res.size(); i++) {
        if (i != 0)printf(" ");
        printf("%d", res[i].key);
    }
    printf("\n");
    for (int i = 0; i < res.size(); i++) {
        if (i != 0)printf(" ");
        printf("%d", res[i].value);
    }
}

总结

之前是为了准备浙大软院的机试刷了PAT甲级真题和近几年的模拟卷，总体来说今年的难度比较低，第一题会有点坑人，其他三题能在1小时内AC。最后我做了2小时不到拿到100分，当时已经有近90个满分，最后一共有400+考生满分。第一次考PAT即毕业。

不过今年浙大软院不能用PAT抵机试了，还是有点坑。客观来说练习PAT对浙大软院机试有很大的帮助，后来的机试我也获得了比较好的成绩，可惜最后还是没有去浙大。

---

个人博客：https://www.randyzhang.com