vins-mono前端详解（2）——imu预积分

原创已于 2023-11-10 20:08:15 修改 · 897 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 #人工智能

于 2023-11-10 20:01:22 首次发布

vins-mono详解专栏收录该内容

7 篇文章

订阅专栏

文章介绍了vins-mono中imu预积分的必要性、原理，包括连续imu积分公式、预积分的引入、误差状态卡尔曼滤波的应用，以及如何计算协方差和雅克比矩阵更新。重点在于理解步骤目的和关键思想，而非复杂的数学推导。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

在vins-mono中将相机和imu进行紧耦合，优化出相对准确的位姿信息。在前端准备工作中，相机采集的图像经过光流追踪获得每一帧图像的特征点信息，而imu所做的准备工作就是预积分。预积分全部内容在integration_base.h文件中，整个文件代码量并不大，这部分主要是数学公式推导比较核心。接下来我会对imu预积分的全部过程进行详细梳理。

imu预积分

目的

在正式进行预积分流程梳理之前需要明确目的：为什么进行imu预积分?而不是积分。

回答这个问题需要清楚整个vins-mono后端优化的原理，vins-mono是把两帧图像之间的imu积分量作为约束条件，进而优化滑窗内的位姿。既然作为一种约束条件，那么就不能随着优化结果而改变，必须相对独立。而对于一般情况，imu获得的两帧之间的积分值是依赖于头一帧imu所在世界坐标系下的位姿的，而这个位姿又恰恰是需要进行优化的，显然直接积分没有办法作为约束。所以引出了预积分，预积分项可以保证和积分区间和左右边界的位姿无关，可以作为优化的约束条件使用。

连续形式的imu积分公式

预积分的引入也是根据连续形式的积分得到的，首先对于连续形式的imu积分公式如下，可以分为位置P、速度V和姿态Q的更新：

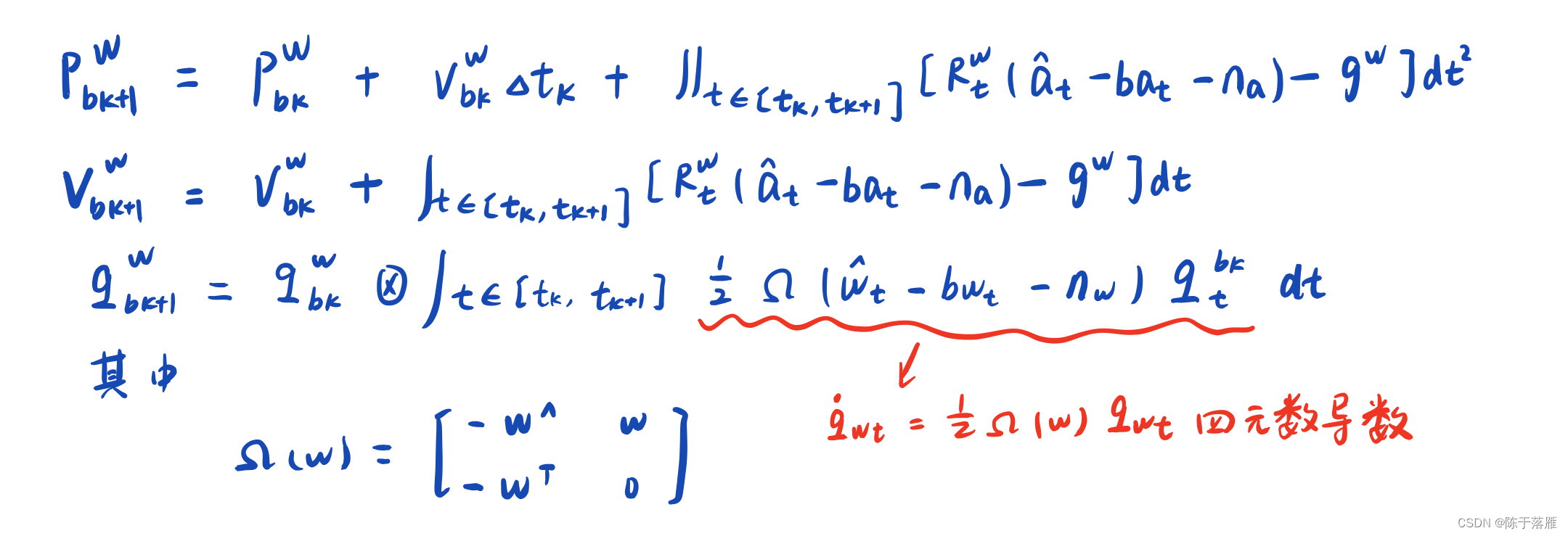
连续形式下的imu积分中包含t时刻和世界坐标系相关的常数项，这就是说如果位姿经过优化以后，积分项的值要重新计算一遍。

预积分的引出

预积分的引出比较巧妙，在上述连续积分式子左右同时乘以从imu系到世界系的坐标系变换矩阵，经过整理就可以得到下式：

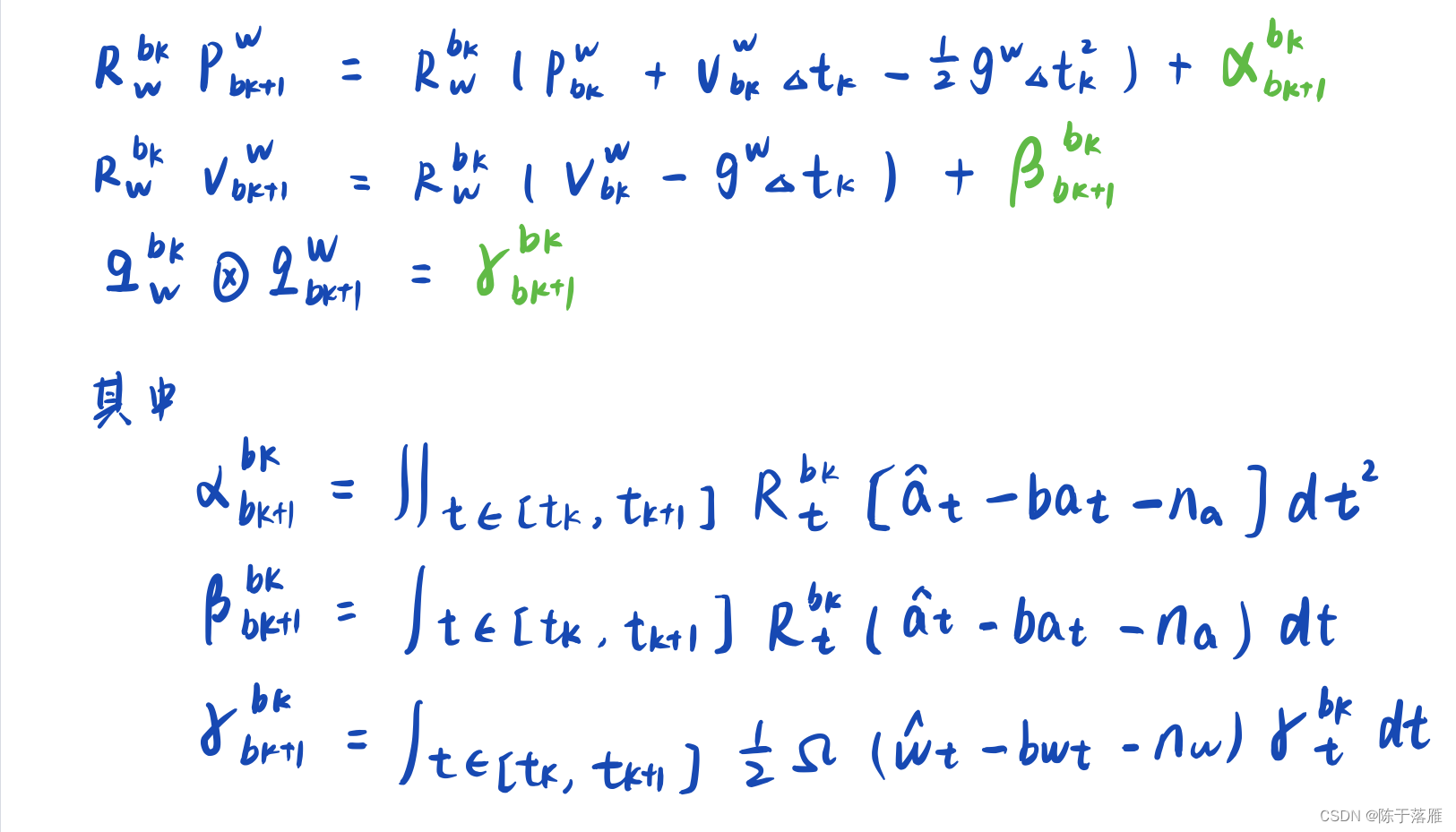
绿色的三个就是预积分值，分别是位置、速度和姿态。可以看到，下一帧的预积分量只和上一帧姿态有关，而和世界坐标系下的位姿无关，预积分量像一个固定的弹簧，约束着左右两帧图像帧的位姿。

预积分量是计算两帧图像帧之间所有的imu积分量，得到的实际是imu经过积分运算后的均值，至于这些均值的置信度是什么样仍然没有求解，我们知道肯定是越积分越不准（置信度越低），那么到底有多么大的置信度就需要进行协方差运算了。

如何计算协方差

什么是ESKF

ESKF（误差状态卡尔曼），在进行卡尔曼滤波时输入的观测值为误差值。具体原理可以参考古月居的这篇帖子，也是对文献[1]的翻译讲解，关于系统状态量的名义值、真实值和误差都有具体说明。在vins-mono中误差状态传递的推导都是基于该理论进行的，简单理解就是真实状态等于名义状态加误差。

在imu预积分这部分，名义值就是imu获得的数据直接进行预积分得到的值，真实值是待求的，误差状态是要使用的中间量。

为什么引出ESKF

用ESKF而不是普通的线性卡尔曼滤波器或者其他类型的卡尔曼滤波器是因为在slam系统里面该滤波器有以下4个优势：

旋转的误差状态是一个很小的值，此时参数数目和自由度数目相同。（释：在小范围内旋转向量没有周期性，之所以使用旋转向量表示而不是四元数是因为四元数存在过参数化，用四个量表示三个自由度的旋转，这会导致得到的协方差矩阵没办法使用）
误差状态和观测的误差都接近0，这样能避免万向节死锁，同时在0附近进行线性化也更加合理可靠
误差量小，二阶导可以忽略，雅克比矩阵计算也更加方便
误差状态变化平缓，卡尔曼滤波器修正频率不需要太高

连续时间imu误差状态传递推导

连续型imu误差状态传递公式是误差状态导数和自身的关系，得到这个导数关系是为了求解离散时间预积分的误差状态传递，进而求出预积分的协方差矩阵。

连续时间imu误差状态传递公式如下：·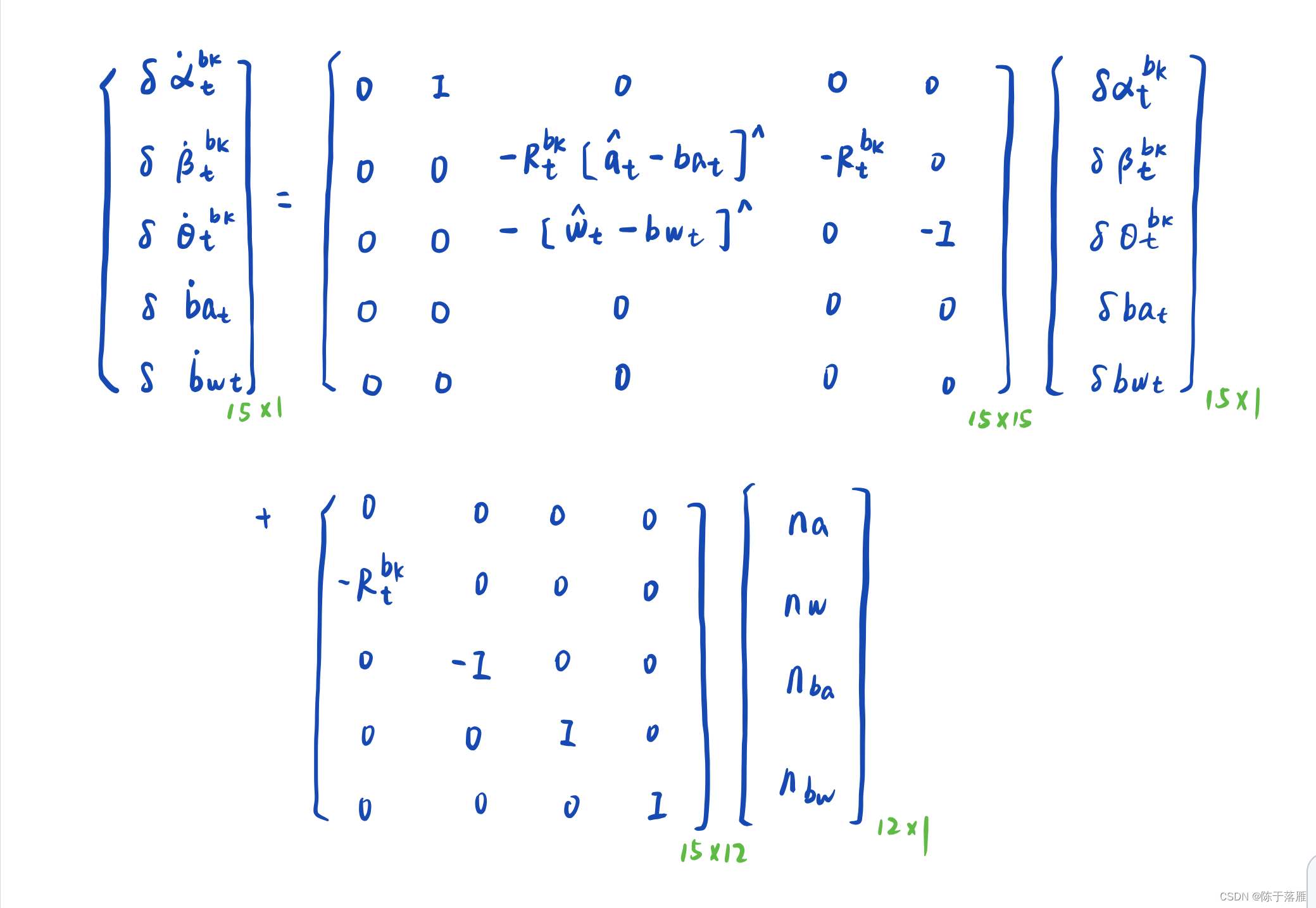

上面5组方程的推导都是基于名义值、真实值和误差值的关系：

基于中值积分计算离散时间预积分误差传递

上面推导出了连续形式的imu误差状态传递公式，而在实际收到的imu数据都是离散形式的，因此应该求出离散形式下的imu误差状态传递公式，以此计算预积分的协方差矩阵。

具体说就是求出前一步的误差状态和后一步误差状态的关系推导，具体实现是用泰勒公式。在上一部分相当于已经求解出了误差状态关于时间的导数，先把上式表达成以下公式表示：

$\Delta \dot{x}=F_{t}\Delta x+G_{t}n_{t}$

然后根据泰勒展开，即可得到下面的递推公式：

$\Delta x_{k+1} = \Delta x_{k}+\Delta \dot{x_{k}}\Delta t$

经过整理可得以下形式的公式：

$\Delta x_{k+1}=(I+F_{t}\delta t)\Delta x_{k}+G_{t}\Delta t*n_{t}$

具体展开形式如下：

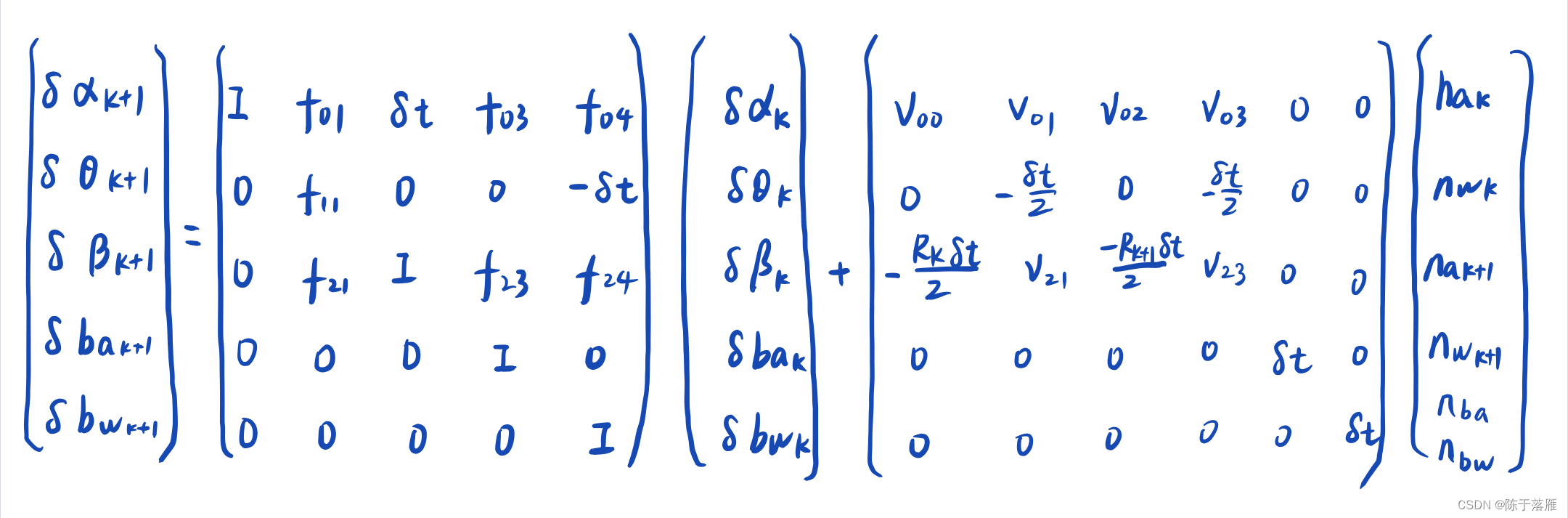
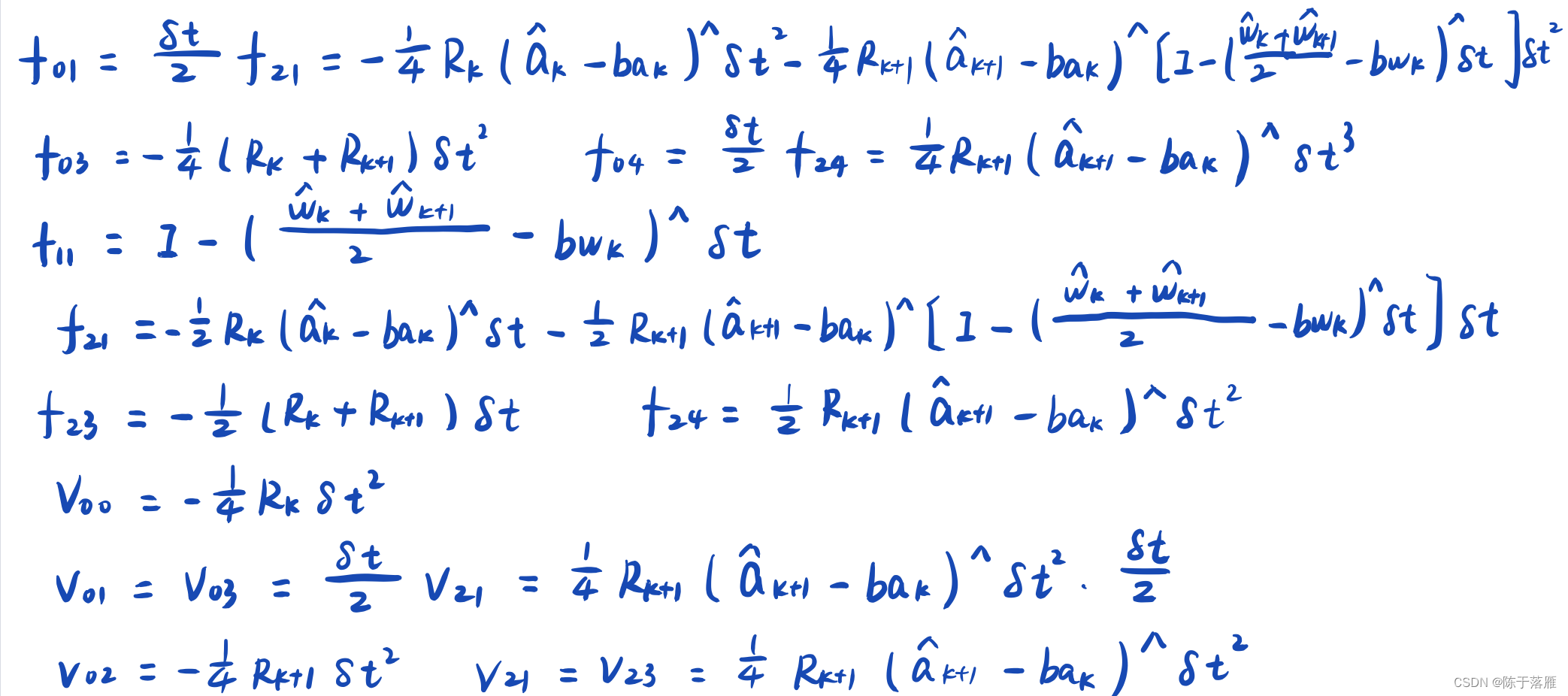
根据展开的泰勒公式推导过程中两帧之间涉及到状态量都采用的是中值法，在程序设计中需要先计算旋转的均值，然后再计算加速度、角速度的均值。具体推导这里不详细展示了，有兴趣的可以私聊我。

把上面离散形式的误差状态传递可以总结成以下形式：

$\Delta x_{k+1}=F\Delta x_{k}+G_{n}$

该公式有利于对预积分的协方差矩阵进行推导。

预积分中关于imu零偏的建模

预积分中有关于imu零偏的项参与计算，然而，在前端预积分中零偏并没有参与积分计算，这并不是我们不想这么做，而是前端属于松耦合没有关于零偏的先验信息，所以在预积分部分零偏项的值为0。不过，在初始化部分我们是可以通过视觉imu的耦合获得陀螺仪的零偏，在那部分是把涉及到的预积分项重新计算了一遍。因为只是初始化部分，这么做也还无伤大雅，然而，加速度计的零偏是耦合在后端优化中的，需要经过优化获得，这个时候如果还是重新计算预积分那就太复杂了，所以才有了这部分的零偏补偿。

实际做法也是和泰勒展开类似，用相关参数项对偏置的雅克比乘以偏置的变化量补偿到原状态量上即可。预积分的零偏补偿如下：

$\alpha _{b_{k+1}}^{b_{k}}\approx \hat{\alpha }_{b_{k+1}}^{b_{k}}+J_{b_{a}}^{\alpha }\Delta b_{a_{k}}+J_{b_{w}}^{\alpha }\Delta b_{w_{k}}$

$\beta _{b_{k+1}}^{b_{k}}\approx \hat{\beta} _{b_{k+1}}^{b_{k}}+J_{b_{a}}^{\beta }\Delta b_{a_{k}}+J_{b_{w}}^{\beta }\Delta b_{w_{k}}$

$\gamma _{b_{k+1}}^{b_{k}}\approx \hat{\gamma }_{b_{k+1}}^{b_{k}}\bigotimes \begin{bmatrix} 1\\ \frac{1}{2}J_{b_{w}}^{\gamma }\Delta b_{w_{k}}\end{bmatrix}$