SDU程序设计思维Week16-CSP M4

最新推荐文章于 2022-07-11 00:00:00 发布

原创最新推荐文章于 2022-07-11 00:00:00 发布 · 578 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#程序设计

本文解析了SDU程序设计竞赛中的三个问题：TT数鸭子，ZJM要抵御宇宙射线，以及宇宙狗的危机。涵盖了算法设计，数据结构应用，以及区间DP等关键概念。通过具体代码示例，深入探讨了解决方案和总结。

SDU程序设计思维Week16-CSP M4

A - TT数鸭子

Description

在这里插入图片描述

Sample

Input:
6 5
123456789 9876543210 233 666 1 114514

Output:
4

Idea

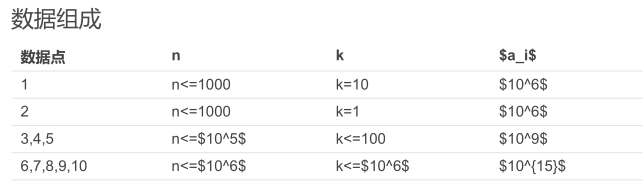
题意：判断一个数的个位、十位、百位……相互之间有多少个不同的数，这个数量小于k表明这个数符合要求

输入每个数，用longlong存储
用vis数组记录0-9是否出现过
每次取一个数的最低位判断并更新vis

Summary

这题不难，比赛中T了5个，卡在了STL和cin。也可以将每个数用string存储，用整型存储要注意数据范围

Codes

#include <iostream>
#include <set>
#include <string>
using namespace std;
long long n, k;
int vis[10];

int main()
{
	long long ans = 0;
	scanf("%lld%lld", &n, &k);
	for (long long i = 1; i <= n; i++) {
		memset(vis, 0, sizeof(vis));
		long long t;
		long long x;
		int num = 0;
		scanf("%lld", &t);
		while (t > 0) {
			x = t % 10;
			if (vis[x] == 0) { vis[x] = 1; num++; }
			if (num >= k)break;
			t = t / 10;
		}
		if (num < k)ans++;

	}
	printf("%lld\n", ans);
}

B - ZJM要抵御宇宙射线

Description

在这里插入图片描述

Sample

Input:
5
0 0
0 1
1 0
0 -1
-1 0
Output:
0.00 0.00
1.00

Idea

题意：求包含所有发射点的以某个发射点为圆心的最小圆

自定义结构体point，包括点的坐标xy以及以该点为圆心包含所有点的圆的半径平方dis
将所有发射点两两求欧式距离，更新两点的dis
按照题目规则将n个点排序，第一个点就是要求的点

Summary

这题枚举所有发射点两两之间的距离即可，注意如果使用iomanip保留两位小数，变量要用double类型

Codes

#include <iostream>
#include <algorithm>
#include <iomanip>
using namespace std;
int n;

struct point {
	double x, y;
	double dis=0.0;
	bool operator<(const point& p) const {
		if (dis != p.dis)return dis < p.dis;
		else if (x != p.x)return x < p.x;
		else return y < p.y;
	}
}p[1010];

int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> p[i].x >> p[i].y;
	}

	for (int i = 1; i <= n; i++) {
		double x = p[i].x, y = p[i].y;
		for (int j = i + 1; j <= n; j++) {
			double r = pow(x - p[j].x, 2) + pow(y - p[j].y, 2);
			if (r > p[i].dis)p[i].dis = r;
			if (r > p[j].dis)p[j].dis = r;
		}
	}
	sort(p + 1, p + 1 + n);

	cout << setiosflags(ios::fixed) << setprecision(2) << p[1].x << " " << p[1].y << endl;
	cout << setiosflags(ios::fixed) << setprecision(2) << p[1].dis << endl;


}

C - 宇宙狗的危机

Description

在这里插入图片描述

Sample

Input:
1
6
3 6 9 18 36 108
Output:
Yes

Input:
2
2
7 17
9
4 8 10 12 15 18 33 44 81
Output:
No
Yes

Idea

题意：将一组升序数组成二叉搜索树，要求任意树边的两端的最大公约数大于1

初始化边集e，表示任意两个数能否满足要求连成边
确定状态t
t[i][j][0] 表示以i为根，[j][i-1]为左子树
t[i][j][1] 表示以i为根，[i+1][j]为右子树
状态转移方程
对于区间[i，j]，分别判断i-1与j+1能否加入二叉搜索树（和对应边集求或），其中k属于[i，j]
t[i-1][j][1] |= e[i-1][k]
t[j+1][i][0] |= e[j+1][k]
最后根据t，判断以各个数为根能否组成二叉搜索树

Summary

这是一道区间DP的问题，以各个数为根试图构造它的左子树与右子树。
比赛中用了DFS求树，T了4个，根据数据范围700，时间复杂度至少要O(n^3)

Codes

#include <iostream>
#include <cstring>
using namespace std;
int T,n;
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a%b); }
int t[720][720][2],e[720][720];
int a[720];
bool flag = false;

int main()
{
	cin >> T;

	while (T--) {
		memset(t, 0, sizeof(t));
		flag = false;
		cin >> n;
		for (int i = 1; i <= n; i++)
			cin >> a[i];

		for(int i=1;i<=n;i++)
			for (int j = 1; j <= n; j++) {
				if (i == j)e[i][j] = 0;
				else e[i][j] = gcd(a[i], a[j]) > 1 ? 1 : 0;
			}

		for (int i = 1; i <= n; i++)
			t[i][i][0] = t[i][i][1] = 1;

		for(int j=1;j<=n;j++)
			for(int i=j;i>=1;i--)
				for (int k = i; k <= j; k++) {
					if (t[k][i][0] && t[k][j][1]) {
						t[i - 1][j][1] |= e[i - 1][k];
						t[j + 1][i][0] |= e[j + 1][k];
					}
				}

		for (int i = 1; i <= n; i++) {
			if (t[i][1][0] && t[i][n][1])
			{
				printf("Yes\n");
				flag = true;
				break;
			}
		}
		if (!flag)printf("No\n");


	}
}