蓝桥杯 2017第八届国赛c/c++b组第4题 发现环（并查集+set)

/*

标题：发现环

小明的实验室有N台电脑，编号1~N。原本这N台电脑之间有N-1条数据链接相连，恰好构成一个树形网络。
在树形网络上，任意两台电脑之间有唯一的路径相连。

不过在最近一次维护网络时，管理员误操作使得某两台电脑之间增加了一条数据链接，于是网络中出现了
环路。环路上的电脑由于两两之间不再是只有一条路径，使得这些电脑上的数据传输出现了BUG。

为了恢复正常传输。小明需要找到所有在环路上的电脑，你能帮助他吗？

输入

第一行包含一个整数N。
以下N行每行两个整数a和b，表示a和b之间有一条数据链接相连。

对于30%的数据，1 <= N <= 1000
对于100%的数据, 1 <= N <= 100000， 1 <= a, b <= N

输入保证合法。

输出

按从小到大的顺序输出在环路上的电脑的编号，中间由一个空格分隔。

样例输入：
5
1 2
3 1
2 4
2 5
5 3

样例输出：
1 2 3 5

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

分析：1.并查集 2.set
运用并查集插入边的信息。（插入时判断该边的两个结点是否已经在一个集合）
如果该边的两个结点a，b不在一个集合，将大的连接到小的上，比如:a<b,node[b]=a;
否则，环路的起始节点begin和结尾结点end就是a和b
边插入完后，将begin节点到根节点的路径中的节点都加入到set
此时分两种种情况:
1.end在begin到根节点路径上
直接输出环

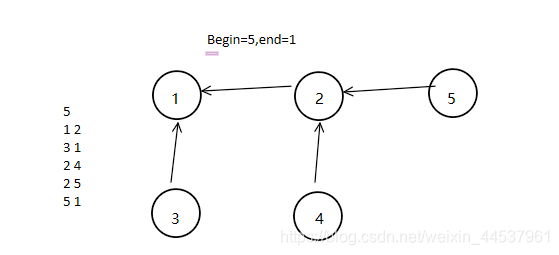
2.end不在根节点的路上，
寻找begin和end到根节点路上的共同结点（图1共同节点为1，图2共同结点为2）。
清空set
将begin和end到共同结点路径上的结点加入到set
输出set

*/

#include<iostream>
#include<set>
#include<algorithm>
#define MAX_N 100000 +10
using namespace std;
int n,node[MAX_N],result[MAX_N];
set<int>set_;	//应用set排序和查重 
set<int>::iterator it;	 
int begin,end,ok;
/*
	初始化节点 
*/ 
void init()
{
	for(int i=0;i<=n;i++)
	node[i]=i;
}
/*
	查找结点x所在集合的根节点 
*/ 
int find(int x)
{
	if(x==node[x])
	return x;
	return find(node[x]);
}
/*
	查看x和y是不是一个集合 
*/
bool same(int x,int y)
{
	return find(x)==find(y); 
}
/*
	连接节点x和节点y
	如果x和y在一个集合中，begin和end等于x，y 
	如果不在一个集合，将大的连接到小的上 
*/
void unite(int x,int y)
{
	if(same(x,y))
	{
		begin=x,end=y;
	}
	else
	if(x<y)
	node[y]=x;
	else
	node[x]=y;
}
/*
	寻找环路径上的节点 
*/
int find_(int x,int z)
{
	it=set_.find(x); 
	if(it!=set_.end())
	{
		return *it;
	}
	if(x==z)
	{
		ok=1;
		set_.insert(x);
		return x;
	}
	if(x==node[x])
	{
		set_.insert(x);
		return x;
	}
	else
	{
		set_.insert(x);
		find_(node[x],z);
	}
}
int main()
{
	int a,b;
	cin>>n;
	init();
	for(int i=0;i<n;i++)
	{
		cin>>a>>b;
		if(begin==0)
		{
			unite(a,b);
		}
	}
	a=find_(begin,end);
	if(!ok)
	{
		b=find_(end,1);
		set_.clear();
		find_(begin,b);
		find_(end,b);
	}
	for(it=set_.begin();it!=set_.end();it++)
		{

		cout<<*it<<" ";
	}
return 0;
}