2019牛客暑期多校训练营（第一场）A Equivalent Prefixes-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_44521786/article/details/96713534

本文介绍了一种利用二分法解决RMQ（区间最小值查询）问题的方法，并详细解释了如何通过比较两组数据的前缀笛卡尔树来判断其是否等价。笛卡尔树被用于构建数据结构，通过二分查找优化了查询效率。

题目：
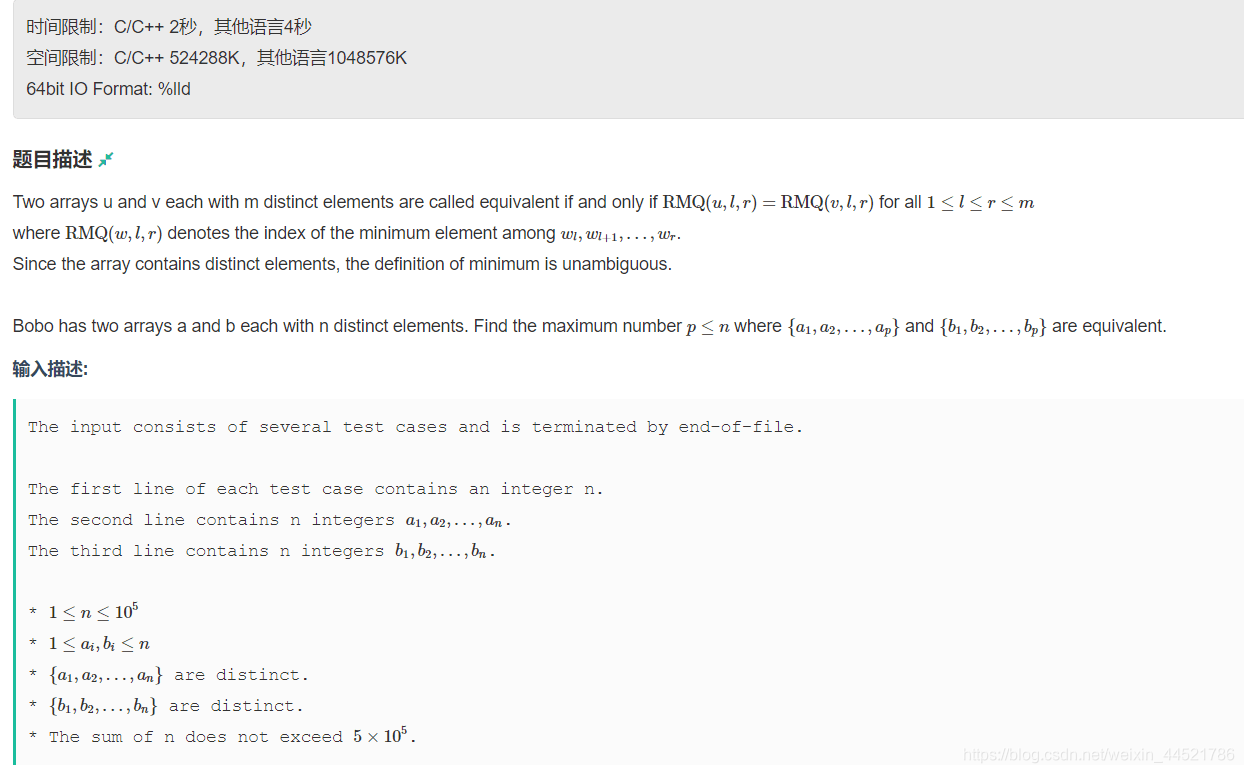
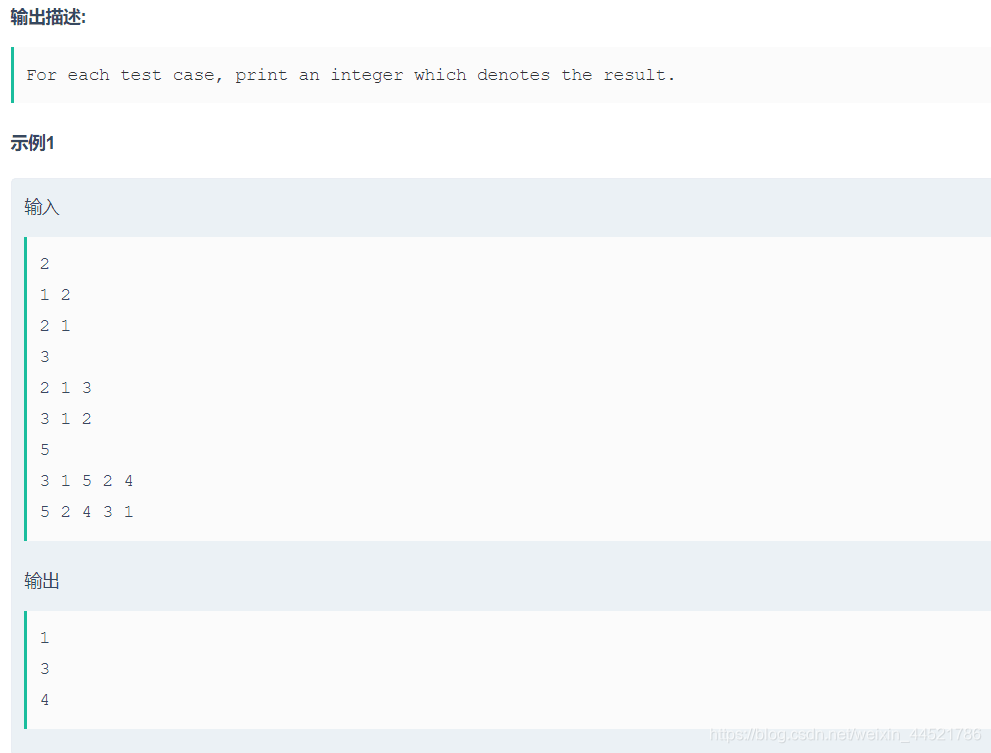
在这里插入图片描述

比赛的时候刚开始都错题和队友wa了三发
后来读懂题目感觉可以用单调栈或者二分
确实都可以

二分：
据说题目所要求的RMQ即笛卡尔树
所以题中的“equivalent”等价于笛卡尔树相同
二分答案，比较两个前缀的笛卡尔树即可
复杂度 O(n log n)
（你要问我什么叫笛卡尔树我也不知道所以学习了一下
贴上百度百科笛卡尔树
维基百科Cartesian tree
和大佬的博客笛卡尔树Cartesian Tree

下面是我的代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
const int maxn = 1e5+10;
int da[maxn],db[maxn];
int fa[maxn],fb[maxn];
int a[maxn],b[maxn];
void calc(int a[],int fa[],int d[],int n){
    stack<int>sta;
    for (int i=n;i>=1;--i){
        while (sta.size()>0&&a[i]<sta.top()) sta.pop();
        sta.push(a[i]);
        if (sta.size()>1) {
            int tmp = sta.top();sta.pop();
            fa[i] = d[sta.top()];
            sta.push(tmp);
        }
        else fa[i] = -1;
        //cout<<i<<" "<<fa[i]<<endl;
    }
}
int main (){
    int n;
    while (~scanf("%d",&n)){
        for (int i=1;i<=n;++i) {
            scanf("%d",&a[i]);
            da[a[i]] = i;
        }
        for (int i=1;i<=n;++i) {
            scanf("%d",&b[i]);
            db[b[i]] = i;
        }
        int l=1,r=n,mid,ans=1;
        while (l<=r) {
            mid = (l+r)>>1;
            calc(a,fa,da,mid);
            calc(b,fb,db,mid);
            int fg=0;
            for (int i=1;i<=mid;++i) {
                if (fa[i] != fb[i]) {
                    fg=1;
                    break;
                }
            }
            if (!fg) l=mid+1,ans=mid;
            else r = mid-1;
        }
        cout<<ans<<endl;
    }
    return 0;
}