动手学深度学习 -- 3.4 Softmax回归

Softmax回归

Softmax回归主要解决深度学习中的分类问题。

问题假设

假设：我们有许多照片，这些照片只包含猫、狗、鸡，则定义表示猫的向量为（1，0，0），表示狗的向量为（0，1，0），表示鸡的向量为（0，0，1）。
【特别注意：这里只考虑一张照片只存在一个动物的情况，不包含一张照片既有猫，又有狗】

模型建立

之后我们建立softmax模型。假设我们的图片是2x2的大小，用来分辨三个种类（猫狗鸡），则有了如下的四个输入，三个输出的softmax模型。

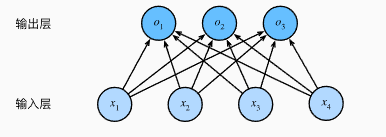
输出层计算

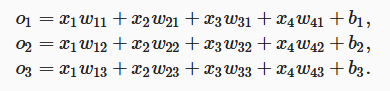
Softmax回归层

这样得到的 $o_1$ 是 $[-\infty ,\infty ]$的值，我们需要将该值缩放到范围$[0,1]$内。
因此引入Softmax回归层，将值约束到$[0,1]$内。

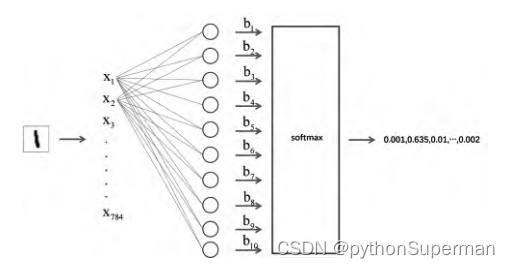
softmax运算符（softmax operator）解决了以上两个问题。它通过下式将输出值变换成值为正且和为 1 的概率分布：

$${\hat{y}}_1,{\hat{y}}_2,{\hat{y}}_3=\mathrm{softmax}\left(o_1,o_2,o_3\right)$$

其中

y^1=exp⁡(o1)∑i=13exp⁡(oi),y^2=exp⁡(o2)∑i=13exp⁡(oi),y^3=exp⁡(o3)∑i=13exp⁡(oi)\hat{y}_{1}=\frac{\exp \left(o_{1}\right)}{\sum_{i=1}^{3} \exp \left(o_{i}\right)}, \quad \hat{y}_{2}=\frac{\exp \left(o_{2}\right)}{\sum_{i=1}^{3} \exp \left(o_{i}\right)}, \quad \hat{y}_{3}=\frac{\exp \left(o_{3}\right)}{\sum_{i=1}^{3} \exp \left(o_{i}\right)}y^​1​=∑i=13​exp(oi​)exp(o1​)​,y^​2​=