检索与散列技术-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_44496230/article/details/96137844

在这里插入图片描述

ASL

ASL：平均检索长度，检索时的平均比较次数
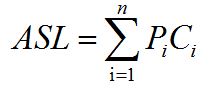
在这里插入图片描述
P_i检索i个元素的概率，C_i检索第i个元素的比较次数

基于线性表的检索

顺序检索

template<class T>
int SeqSearch(vector<Item<T>*>&datalist, int length, const T &K)
{
	int i=length;
	datalist[0]->setKey(K);
	//datalist[0]设置为监视哨，循环不需要再比较i>=0,加速程序
	while(datalist[i]->getKey()!=K)
	{
		i--;
	}
	return i;
}

顺序检索ASL

成功检索的平均比较次数为(n+1)/2
失败检索的比较次数为(n+1)
设检索成功的概率为p，总的平均检索长度为(n+1)(1-p/2)，即(n+1)/2<ASL<n+1

加快顺序检索

根据预期的访问概率由高到低排列记录；
调换方法：把找到的记录与它在线性表中的前一个记录交换位置
移至前端（链表实现）：把找到的记录放在线性表的最前端

二分检索（有序表,顺序存储）

检索成功或检索区间为0检索不成功
用二分检索的决策树分析二分检索的性能，这是一个二叉搜索树BST，对于同长度的有序数组，其下标组成的BST都一样

二分检索ASL

log₂(n+1)-1

分块检索

把线性表分成若干块，每一块中次序任意，前一块中的所有关键码都小于（大于）后一块中的所有关键码；
建立一个索引表，存储每块中最大（最小）的关键码值&块的起始位置，该索引表是有序表
索引中检索可以采用顺序检索或二分检索，块中检索采用顺序检索

分块检索ASL

（表分成b块，每块s个记录，共n个记录）

索引表用二分检索：
ASL= [log₂(b+1)-1]+(s+1)/2 = log₂((n/s)+1)+(s-1)/2
索引表用顺序检索：
ASL= (b+1)/2+(s+1)/2 = (n+s²)/2s+1
(s取根号n，达到最小)

性能介于二分检索和顺序检索之间；

插入时找到属于的块，插入块尾；
删除时，如果删除的不是最后一个记录，把最后一个记录填入删除的位置

集合的检索

集合中的元素各不相同，次序无关紧要。
vector<bool>来表示集合
bitset表示集合

散列方法

在这里插入图片描述

散列（哈希）

散列表的存储空间是一个一维数组，散列地址是数组的下标；
散列不适合基于磁盘的应用，不适合范围查询；
散列ASL不依赖于散列表中元素个数，而是随负载因子（N/M）的增大而增大；
当负载因子<0.5，大部分情况下检索长度小于2；负载因子超过0.5，散列表的性能就会显著下降

散列函数的原则：

运算尽可能简单；
函数的值域必须在散列表范围内；
尽可能使结点分布均匀；
不同的关键码拥有不同的散列函数值

散列函数构造法	阐述	参数取值	优点	缺点
除余法	关键码%M	M常取散列表长度，或小于散列表长度的最大质数	M不必是一个常数，其值可以在程序运行时确定	连续的关键码散列成连续的散列值
乘余取整法	(关键码xA%1)xn向下取整	（0<A<1）A一般取黄金分割最理想A=(根号5-1)/2 ；若地址空间为p，n=2^p
平方取中法	关键码²,根据散列表的长度取其值的中间几位		乘积中间的几位数和乘数的每一位都相关，产生的散列地址比较均匀；整数相乘的速度比相除快；最接近于随机化
数字分析法			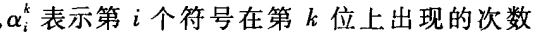选计算出的值较小的几位作为散列值，表示在该位符号分布地均匀
基数转换法	把关键码值看成另一种进制的数，再转换成原来进制的数，选取其中几位作为散列地址	两个基数互素，新基数比原基数大
折叠法	关键码分割成位数相同的几部分，取这几部分的叠加和作为散列地址	移位叠加，分界叠加

冲突解决方法

在这里插入图片描述

开散列方法

开散列方法效率最高，实际系统中使用的散列大多是开散列。

拉链法：

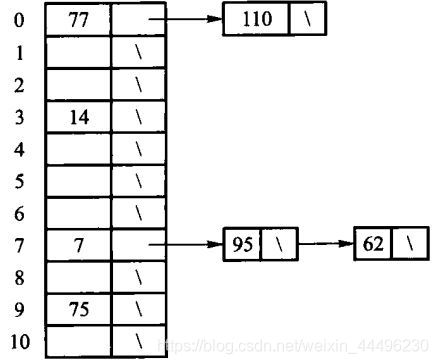
在这里插入图片描述

同义词记录可以按照多种方式排列：输入顺序、值的顺序、访问频率顺序
适合散列表存储在内存，不适合存储在磁盘

桶式散列

每个存储桶包含一个或多个页块，每个页块包含多个记录，一个桶内的各页块用指针连起来。散列函数把关键码值散列成桶号。桶目录表存储桶内第一个页块的地址。
适合散列表存储在磁盘

闭散列方法

关键码由散列函数计算出基地址，发生冲突时，为关键码生成探查序列，依照探查序列依次探查，直到找到第一个空闲位置存储记录。

线性探查法

线性探查法将散列表看成一个环形表
基本聚集（聚集）：基地址不同的关键码，争夺相同的后继散列地址。（散列函数选择不当或者负载因子过大）
改进线性探查：每次跳过c个槽，而不是1个槽。（c与散列表长互素，任何关键码的探查序列都能走遍所有的槽）

二次探查法

探查序列依次为：1²，-1²，2²，-2²，3²……发生冲突时，将同义词来回散列在基地址的两端。
缺点：不能探查到整个散列表的所有位置
优点：后继散列地址不是连续的，而是跳跃的，为后续元素留下空间，减少聚集。

随机探查法

理想的探查序列应该在从未访问过的槽中随机选择下一个位置，但实际上不能真正随机地选择，因为检索关键码的时候不能建立同样的探查序列。
设置伪随机探查序列，插入和检索都采用相同的伪随机数（避免产生0和散列表长，因为导致对基地址的探查，多做一次无效操作）

双散列探查法

二级聚集：伪随机探查、二次探查都能消除基本聚集。但是散列到同一个基地址的关键码，仍会得到同样的探查序列。
因为随机探查和二次探查产生的探查序列只是基地址的函数，而不是关键码值的函数。
双散列探查法：第二个散列函数的值（尽量与散列表长度互素）作为线性探查的常数项
使得散列函数值与线性表长度M互素：

M取素数；
M取2^m,散列值取1~2^m-1之间的奇数
M取任意数，h₁(K)=K%p(p是小于M的最大素数)，h₂(K)=K%q+1(q是小于p的最大素数)，虽然不能保证h₂(K)与M互素，但很常用。

**缺点：**计算量大一些
**优点：**最接近随机分布

散列表删除元素

设置一个特殊的标志位，记录散列表中的单元状态（空单元、单元被占用、已删除（墓碑TOMB））
检索时：如果遇到TOMB，顺着探查序列继续进行，直到检索到关键码或遇到空单元为止。
插入时：如果遇到TOMB，记下第一个TOMB的位置，为了避免插入两个相同的关键码，顺着探查序列继续检索，如果发现了相同的关键码，插入失败；整个探查序列都探测完毕，在第一个TOMB处插入新关键码。