David Silver Lecture 4 | Model-Free Prediction

参考：https://zhuanlan.zhihu.com/p/28107168

1. Introduction

本节课：给定Policy估计价值函数
下节课：不断更新（优化）价值函数

这节课的目的是Model-free prediction，即Estimate the value function of an unknown MDP (在给定Policy下估计价值函数)。下节课我们考虑Model-free control（最优化价值函数）。

model-free : 无MDP Transition $\mathcal{P}$ / Rewards $\mathcal{R}$

2. Monte-Carlo Learning

蒙特卡洛强化学习指：在不清楚MDP状态转移及即时奖励的情况下，直接从经历完整的Episode（即Agent与Environment交互直到终止状态）来学习状态价值，通常情况下某状态的价值等于在多个Episode中以该状态算得到的所有收获的平均。

完整的Episode 指必须从某一个状态开始，Agent与Environment交互直到终止状态，环境给出终止状态的即时收获为止。

• 目的： 在给定Policy下，估计该Policy下的价值函数$v_{\pi }$。
• 回顾：
  • Return $G_t=R_{t+1}+\gamma R_{t+2}+...+{\gamma }^{T-1}{R}_T$
  • Value function $v_{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$
• 想法：
  • 我们并不一定要严格地通过期望的计算得到Value Function，而是用Empirical Mean。

有两种方法可以实现这个想法：
这两种想法的区别在于对于同一个Episode，经过同一个状态$s$多次是否要更新多次。

2.1 First-Visit Monte-Carlo Policy Evaluation

• 假设我们要在Policy$\pi$下Evaluate state $s$
• 因为我们在一次Episode里面可能有多次经过这个state，我们只考虑第一个时刻$t$ (对应方法的名字：Fist-Visit)
• $N(s)\leftarrow N(s)+1$，$S(s)\leftarrow S(s)+G_t$
• $V(s)=\frac{S(s)}{N(s)}$
• 这里的N(s)是累计的，即考虑多个Episode。
• 由大数定理我们有$V(s)\to v_{\pi }(s),N(s)\to \infty$

2.2 Every-Visit Monte-Carlo Policy Evaluation

• 假设我们要Evaluate state $s$
• 因为我们在一次Episode里面可能有多次经过这个state，我们考虑所有经过State $s$的时刻$t$ (对应方法的名字：Every-Visit)
• $N(s)\leftarrow N(s)+1$，$S(s)\leftarrow S(s)+G_t$
• $V(s)=\frac{S(s)}{N(s)}$
• 这里的N(s)是累计的，即考虑多个Episode。
• 由大数定理我们有$V(s)\to v_{\pi }(s),N(s)\to \infty$

例子：21点 Blackjack

此例子并没有给出策略更新，只是评估这种状态的价值函数

状态空间：
（多达200种，根据对状态的定义可以有不同的状态空间，这里采用的定义是牌的分数，不包括牌型）

1. 当前牌的分数（12 - 21），低于12时，你可以安全的再叫牌，所以没意义。[J,Q,K都看成10点]
2. 庄家出示的牌（A - 10），庄家会显示一张牌面给玩家
3. 我有“useable” ace吗？（是或否）A既可以当1点也可以当11点。

行为空间：

1. 停止要牌 stick
2. 继续要牌 twist

奖励（对停止要牌这个动作）：
+1：如果你的牌分数大于庄家分数
0： 如果两者分数相同
-1：如果你的牌分数小于庄家分数

奖励（对继续要牌这个动作）：
-1：如果牌的分数>21，并且进入终止状态
0：其它情况

状态转换（Transitions）：如果牌分小于12时，自动要牌(twist)

当前策略：牌分只要小于20就继续要牌。

求解问题：
评估该策略的好坏。(事实上当我们知道对于一个State s的$v(s)$的值的时候，我们就大概能猜到是否能赢了，因为我们是取平均值，所以按照奖励设置，Value越大越容易赢）

求解过程：
因为状态空间有三个维度，我们首先区分2种情况：区分玩家手中有无A。

然后，我们对于每种情况，画出庄家显示的牌面值、玩家当前牌面总分值这个二维状态空间中每一个值对应的Value Function。数据的获得是通过统计每一牌局下决定状态的庄家和玩家牌面的状态数据，同时计算其最终收获。通过模拟多次牌局，计算每一个状态下的平均值，得到如下图示。

我们可以具体考虑一种情况，

• 我们的策略是两张牌总和<20就继续加牌
• 庄家手中一张明牌是4
• 玩家手中两张牌和为15，在我们当前的状态下，玩家一定会继续加牌
• 考虑玩家手中无A的情况。

状态价值等于累计总和/次数，如$(1-1+1)/3=0.333$

这里我们给出第一个对局的Episode:

$S_0$	$A_0$	$R_1$	$S_1$	$A_1$	$R_2$
<4,15>	继续要牌	0	<4,20>	停止要牌	1

继续要牌：-1 如果超过21，0 其他情况。
停止要牌：1 如果赢过庄家，0 相等， -1 庄家赢了。

2.3 Incremental Mean

$${\mu }_k={\mu }_{k-1}+\frac{1}{k}(x_k-{\mu }_{k-1})$$

推导：
$$\begin{array}{rl}{\mu }_k& =\frac{1}{k}\sum _{j=1}^k{x}_j\\ & =\frac{1}{k}\sum _{j=1}^{k-1}{x}_j+\frac{1}{k}{x}_k\\ & =\frac{k-1}{k}{\mu }_{k-1}+\frac{1}{k}{x}_k\\ & ={\mu }_{k-1}+\frac{1}{k}(x_k-{\mu }_{k-1})\end{array}$$

直觉：
我们每次拿到一个新的数据都对误差$(x_k-{\mu }_{k-1})$按照一定的比率来对原始估计进行更新。如果原先平均值估计得比现在看到的值更小，则我们新估计的平均值比原来更大一些。

2.4 Incremental Monte-Carlo Updates

对于$S_t$状态进行更新。
$N(S_t)\leftarrow N(S_t)+1$
$V(S_t)\leftarrow V(S_t)+\frac{1}{N(S_t)}(G_t-V(S_t))$

对于Non-Stationary问题，我们并不需要完全记录过去的所有信息，因此我们需要忘记过去的episodes，我们使用alpha
$$V(S_t)\leftarrow V(S_t)+\alpha (G_t-V(S_t))$$

3. Temporal-Difference Learning

时序差分学习简称TD学习，它的特点如下：

• 和蒙特卡洛学习一样，它也从Episode学习，不需要了解模型本身；
• 但是它可以学习不完整的Episode（即Episode不需要终止），通过自身的引导（bootstrapping），猜测Episode的结果，同时持续更新这个猜测。

3.1 Monte-Carlo 和 Temporal-Difference区别

Incremental Every-visit Monte-Carlo目的：
让$V(S_t)$靠近Actual Return $G_t$。

$$V(S_t)\leftarrow V(S_t)+\alpha (G_t-V(S_t))$$

TD(0):
让$V(S_t)$靠近Estimated Return $R_{t+1}+\gamma V(S_{t+1})$。

$$V(S_t)\leftarrow V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1})-V(S_t))$$

其中我们称
TD Target：$R_{t+1}+\gamma V(S_{t+1})$
TD error：${\delta }_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)$

直觉上的区别：
因为我们价值函数设置的关系，Monte-Carlo可能不能体会到“险情”。假如一个人在驾车回家的路上突然碰到险情：对面迎来一辆车感觉要和你相撞，严重的话他可能面临死亡威胁，但是最后双方都采取了措施没有实际发生碰撞。如果使用蒙特卡洛学习，路上发生的这一险情可能引发的负向奖励不会被考虑进去（因为人确实没死），不会影响总的预测耗时；但是在TD学习时，碰到这样的险情，这个人会立即更新这个状态的价值，随后会发现这比之前的状态要糟糕，会立即考虑决策降低速度赢得时间，也就是说你不必像蒙特卡洛学习那样直到他死亡后才更新状态价值，那种情况下也无法更新状态价值。

例子：Driving Home ｜ MC,TD的区别

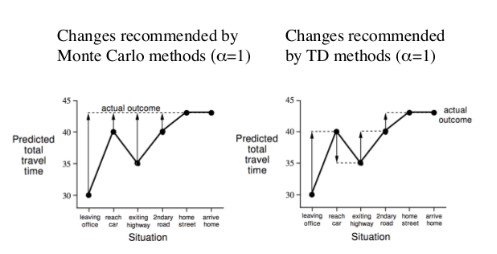
Monte-Carlo的想法是等到一个Episode结束再更新自己之前的猜测。在上面的例子中，就是在进入家门之后，再对每一个状态的预计仍需耗时的估计利用最后真实值43min进行更新。

TD的想法是：
当你离开办公室的时候，因为你还不知道下雨了，你对回家的时间比较乐观，因此估计为30min。
但是下一个状态的时候，你发现下雨了，因此增加了你预测的总耗时。
就这么两个相邻的状态TD就可以对自己的状态进行更新。在图上的表示就是相邻的两个节点，第一个节点根据第二个节点的值进行更新，而不是根据最后的真实值进行更新。

因此，
TD 在知道结果之前可以学习(online)，MC必须等到最后结果才能学习；
TD 可以在没有结果时学习，可以在持续进行的环境里学习。

TD works in continuing (non-terminating) environments.
MC works for episodic (terminating) environments.

3.2 MC和TD区别2 Bias/Variance Trade-off

MC用的$G_t=R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{T-1}{R}_T$，一个unbiased estimate of $v_{\pi }(S_t)$ ，因为$G_t$里面含有很多个状态，因此比TD更Noisy，即方差比TD更大。

真实的TD Target为$R_{t+1}+\gamma v_{\pi }(S_{t+1})$因为使用了真实值$v_{\pi }(S_{t+1})$，所以是Unbiased 的估计。
但是实际上我们使用的是$R_{t+1}+\gamma V(S_{t+1})$，即用了对下一状态价值的估计值，因此是Biased。

总结：

• MC 没有bias，但有着较高的变异性（Variance），且对初始值不敏感；
• TD 低variance, 但有一定程度的bias，对初始值较敏感，通常比 MC 更高效，TD(0) 可以收敛到$v_{\pi }(s)$。

例子：Random Walk

本例子的目的：
比较MC和TD收敛的速度，以及TD能收敛到真实值。

状态空间：

ABCDE中间状态，方块终止状态。只有到达右边的方块才有1的奖励。

行为空间：除终止状态外，任一状态可以选择向左、向右两个行为之一；这里我们评估的状态是左右各50%的概率。

即时奖励：右侧的终止状态得到即时奖励为1，左侧终止状态得到的即时奖励为0，在其他状态间转化得到的即时奖励是0；

状态转移：100%按行为进行状态转移，进入终止状态即终止；

衰减系数：1；(即所有的奖励全部累加在一起)

给定的策略：随机选择向左、向右两个行为。

问题：对这个MDP问题进行预测，也就是评估随机行走这个策略的价值，也就是计算该策略下每个状态的价值，也就是确定该MDP问题的状态价值函数。

结果：

一开始的时候各个状态的价值都被初始化为0.5，我们发现经过100次更新之后，它越来越接近真实值了。

真实值的推导：
鉴于我们的policy是左右各50%的几率，所以
$$\{\begin{array}{c}{x}_a=\frac{0+x_b}{2}\\ x_b=\frac{x_a+x_c}{2}\\ x_c=\frac{x_b+x_d}{2}\\ x_d=\frac{x_c+x_e}{2}\\ x_e=\frac{1+x_d}{2}\end{array}$$
因此$x_a=\frac{1}{6},x_b=\frac{2}{6}...$

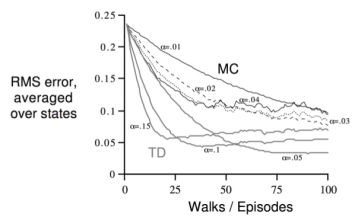
横坐标是经历的Episode数量，纵坐标是计算得到的状态函数和实际状态函数下各状态价值的均方差。黑色是MC算法在不同step-size下的学习曲线，灰色的曲线使用TD算法。可以看出TD较MC更高效。此图还可以看出当step-size不是非常小的情况下，TD有可能得不到最终的实际价值，将会在某一区间震荡。

例子：AB Example

如果Experience足够多(Episode数目足够多)，则不论是MC还是TD对状态s价值的估计$V(s)$都能收敛到真实值$v_{\pi }(s)$。
但是如果我们只给它们有限个episodes（有限个Experience?）让后他们在上面不断地学习，MC和TD会有同样的结果吗？

假设我们只有这8个Episodes，要求你估计A和B这两个状态的价值函数V(A)和V(B)。

MC:
V(A) = 0, V(B) = $\frac{6}{8}$

TD:

V(A) = V(B) = $\frac{6}{8}$
因为从目前来看到达A有100%的概率会到B，而B的价值为0.75。
所以$V(A)=R_{t+1}+V(B)=0+V(B)=V(B)$。

具体来说：
MC算法试图收敛至一个能够最小化状态价值V(s)与实际收获$G_t$的均方差的解决方案，这一均方差用公式表示为：

其中:

• k: episode 序号，一共K个episodes。
• $T_k$: 第k个Episodes的总状态数，每一个t表对应一个状态$S_t$
• $G_t^k$: 第k个Episodes里t时刻状态$S_t$获得的最终收获。

TD算法则收敛至一个根据已有经验构建的最大可能的马儿可夫模型的状态价值，也就是说TD算法将首先根据已有经验估计状态间的转移概率：

上面式子的含义就是在所有Episodes各个时刻找s到s’这个动作的数量除以从s出发的所有动作的总数。

然后因为每次在s我们会用不同的动作a到达不同的状态，因此多次对统一状态的TD(0) $V(s_t)=R_{t+1}+\gamma V(S_{t+1})$实际上就是利用(s,a,s’)这个对当前状态s的价值进行更新。

3.3 MC和TD区别3 Markov Proerty

TD exploits Markov property

• Usually more efficient in Markov environments
  MC does not exploit Markov property
• Usually more effective in non-Markov environments

TD 在Markov environments环境中更有效。

3.4 DP,MC,TD 三种方法总结🌟

Monte-Carlo, Temporal-Difference 和 Dynamic Programming 都是计算状态价值的一种方法。

计算公式：

• MC:
  $V(S_t):=V(S_t)+\alpha (G_t-V(S_t))$
• TD(0):
  $V(S_t):=V(S_t)+\alpha (R_{t+1}+\gamma V(S_{t+1})-V(S_t))$
• MC:
  $V(S_t):={\mathbb{E}}_{\pi }[R_{t+1}+\gamma V(S_{t+1})]$

关于是否需要Model(转移矩阵)：

• MC和TD不需要，DP需要，它通过计算一个状态S所有可能的转移状态S’及其转移概率以及对应的即时奖励来计算这个状态S的价值。
• 此外MC需要完整的Episode才能更新，TD不用。

关于是否Bootstrap：

• MC 没有引导数据，只使用实际收获；DP和TD都有引导数据$V(S_{t+1})$。
• 从某程度上如果episode足够多，$S_t$后续更可能达到的$S_{t+1}$就会更容易到达。实际上就起到了某种加权的作用，类似于在求${\mathbb{E}}_{\pi }$。

关于是否用样本来计算:

• MC和TD都是应用样本来估计实际的价值函数；而DP则是利用模型直接计算得到实际价值函数，没有样本或采样之说。

下面用图表示这三种方法：

• 白点表示状态，黑点表示动作。

MC: 采样，一次完整经历，用实际收获更新状态预估价值

TD：采样，经历可不完整，用喜爱状态的预估状态价值预估收获再更新预估价值

DP：没有采样，根据完整模型，依靠预估数据更新状态价值

放在一张图上

上图从两个维度解释了四种算法的差别，多了一个穷举法(Exhaustive Search)。这两个维度分别是：采样深度(shallow,deep)和广度(full,sample)。当使用单个采样，同时不走完整个Episode就是TD；当使用单个采样但走完整个Episode就是MC；当考虑全部样本可能性，但对每一个样本并不走完整个Episode时，就是DP；当既考虑所有Episode又把Episode从开始到终止遍历完，就变成了穷举法。

需要提及的是：DP利用的是整个MDP问题的模型，也就是状态转移概率，虽然它并不实际利用样本，但是它利用了整个模型的规律，因此认为是Full Width的。

4. TD$(\lambda )$

这是一种将MC和TD融合起来的想法。
$\lambda$是一个加权的参数，特别地
$\lambda =0$ 只考虑第一个动作 TD(0)
$\lambda =1$ 只考虑最后一个动作（整个episodes termintates时候的rewards）MC

注：图中空心大圆圈表示状态，实心小圆圈表示行为

我们采用n-StepPrediction：
1-Step, $G_t^{(1)}=R_{t+1}+\gamma V(S_{t+1})$
2-Step, $G_t^{(2)}=R_{t+1}+\gamma R_{t+2}+{\gamma }^{2}V(S_{t+2})$

n-Step，$G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}V(S_{t+n})$

然后使用：$V(S_t)\leftarrow V(S_t)+\alpha (G_t^{(n)}-V(S_t))$

Rq:

• 这里的$R_{t+1}$是从$S_t$到$S_{t+1}$这个Action带来的Instant Reward。

例子：Large Random Walk | $\lambda$怎么取值最优？

这个示例研究了使用多个不同步数预测联合不同步长(step-size，公式里的系数α）时，分别在在线和离线状态时状态函数均方差的差别。所有研究使用了10个Episode。离线(offline)与在线的区别在于，离线是在经历所有10个Episode后进行状态价值更新；而在线则至多经历一个Episode就更新一次状态价值。

结果如图表明，离线和在线之间曲线的形态差别不明显；从步数上来看，步数越长，越接近MC算法，均方差越大。对于这个大规模随机行走示例，在线计算比较好的步数是3-5步，离线计算比较好的是6-8步。但是不同的问题其对应的比较高效的步数不是一成不变的。因此选择多少步数作为一个较优的计算参数也是一个问题。

Sol: 综合考虑所有step的预测。

4.1 $\lambda$-return

对于不同step (不同n) 的结果进行几何加权。(几个Step就是采取几个动作)

回顾：$G_t^{(n)}=R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}V(S_{t+n})$，一般不会加到$\infty$而是加到$T-t-1$，T是终止状态的时刻步数，t是当前时刻。(所以如果t是T-1,则加到0，即只考虑$R_{t+1}+\gamma V(t+1)$)

然后使用下面的公式进行更新。

Rq:

• 使用几何加权的原因是因为它实现起来方便且计算效率更高。
• 我们可以从两个方向了来理解$TD(\lambda )$

4.2 两个方向理解$TD(\lambda )$

4.2.1 前向认识TD(λ)

引入了λ之后，会发现要更新一个状态的状态价值，必须要走完整个Episode获得每一个状态的即时奖励以及最终状态获得的即时奖励。这和MC算法的要求一样，因此TD(λ)算法有着和MC方法一样的劣势。λ取值区间为[0,1]，当λ=1时对应的就是MC算法。这个实际计算带来了不便。

4.2.2 反向认识TD(λ)

TD(λ)从另一方面提供了一个单步更新的机制，通过下面的示例来说明。

例子：被电击的原因 ｜ Frequency/Recency Heuristic

这是之前见过的一个例子，老鼠在连续接受了3次响铃和1次亮灯信号后遭到了电击，那么在分析遭电击的原因时，到底是响铃的因素较重要还是亮灯的因素更重要呢？

有两种可能的说法：

• 频率启发 Frequency heuristic：将原因归因于出现频率最高的状态，因此我们可能认为是铃铛导致了电击。
• 就近启发 Recency heuristic：将原因归因于较近的几次状态，因此我们可能认为是灯光导致了电击。

因此，我们引入效用追踪（Eligibility Traces, ES，也有翻译成“资质追踪”）

4.3 Eligibility Traces

$E_0(s)=0$
$E_t(s)=\gamma \lambda E_{t-1}(s)+1_{S_t=s}$，如果$S_t=s$则加1。

该图横坐标是时间，横坐标下有竖线的位置代表当前进入了状态s，纵坐标是效用追踪值E。可以看出当某一状态连续出现，E值会在一定衰减的基础上有一个单位数值的提高，此时将增加该状态对于最终收获贡献的比重，因而在更新该状态价值的时候可以较多地考虑最终收获的影响。同时如果该状态距离最终状态较远，则其对最终收获的贡献越小，在更新该状态时也不需要太多的考虑最终收获。

直觉解释就是每个时刻如果有刺激，就增加1，否则就指数递减。

特别的， E值并不需要等到完整的Episode结束才能计算出来，它可以每经过一个时刻就得到更新。 E值存在饱和现象，有一个瞬时最高上限： $E_{max}=\frac{1}{1-\gamma \lambda }$

🌟 🌟 把刚才的描述体现在公式里更新状态价值，是这样的：

$$\begin{array}{rl}{\delta }_t& =R_{t+1}+\gamma V(S_{t+1})-V(S_t)\\ E_t(s)& =\gamma \lambda E_{t-1}(s)+1_{S_t=s}\\ V(s)& \leftarrow V(s)+\alpha {\delta }_t{E}_t(s)\end{array}$$

正常情况下(TD(0))
$$V(s)\leftarrow V(s)+\alpha {\delta }_t$$

所以相当于引入了一个系数，这个系数是对当前状态$s$的频率和就近两个因素的衡量。如果这个系统出现频繁且很近就发生，则我们对误差赋予更多权重，对于当前状态s的价值函数更新就越大。

注：每一个状态都有一个E值，E值随时间而变化。
当λ=0时，只有当前状态得到更新，等同于TD(0)算法；
当λ=1时，TD(1)粗略看与每次访问的MC算法等同；在线更新时，状态价值差每一步都会有积累；离线更新时，TD(1)等同于MC算法。

注：ET是一个非常符合神经科学相关理论的、非常精巧的设计。把它看成是神经元的一个参数，它反映了神经元对某一刺激的敏感性和适应性。神经元在接受刺激时会有反馈，在持续刺激时反馈一般也比较强，当间歇一段时间不刺激时，神经元又逐渐趋于静息状态；同时不论如何增加刺激的频率，神经元有一个最大饱和反馈。

总结